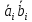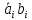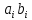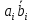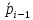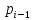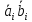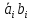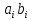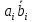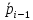ргр 2

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Магнитогорский государственный технический университет им. Г.И. Носова»

Кафедра электротехники и электротехнических систем

РГР №2

на тему: «Разработка и исследование схемотехники n-разрядного сумматора»

Вариант №1

Выполнил:	студент группы АВ-10 Барханова Э.Р.
Проверил:	преподаватель Мугалимов Р.Г.

Магнитогорск 2012

Исходные данные:

2-разрядный параллельный сумматор.

Содержание отчёта:

1. Привести таблицу истинности, булевы уравнения, логическую схему с осциллограммой полного одноразрядного сумматора;

2. Составить логическую схему 2-разрядного сумматора - вычитателя в базисе И-НЕ. Проверить работоспособность сумматора, сняв осциллограммы входных и выходных сигналов;

3. Сделать выводы.

1. Полный одноразрядный сумматор в базисе И, ИЛИ, НЕ

Логическая схема полного одноразрядного сумматора, построенная в базисе И, ИЛИ, НЕ

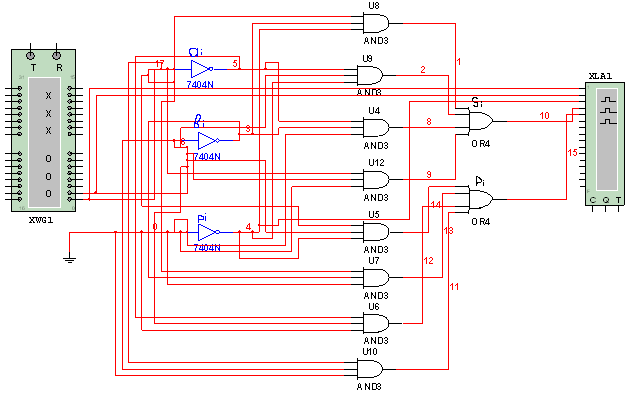
Осциллограмма входных и выходных сигналов полного одноразрядного сумматора (вход сигнала переноса заземлен)

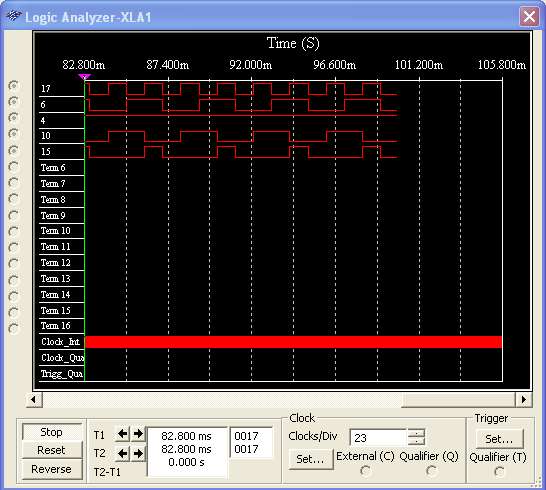
Таблица истинности одноразрядного полного сумматора

№ п/п	Вход				Выход
	pi-1	bi	ai	Si		Pi
0	0	0	0	0		0
1	0	0	1	1		0
2	0	1	0	1		0
3	0	1	1	0		1
4	1	0	0	1		0
5	1	0	1	0		1
6	1	1	0	0		1
7	1	1	1	1		1

Таблица истинности одноразрядного полного сумматора (вход сигнала переноса заземлен)

№ п/п	Вход				Выход
	pi-1	bi	ai	Si		Pi
0	0	0	0	0		0
1	0	0	1	1		0
2	0	1	0	1		0
3	0	1	1	0		1

Булевые уравнения для сигналов суммы и сигнала переноса:

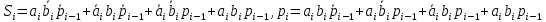
Попробуем произвести минимизацию данных уравнения с помощью карт Карно:

Карта Карно для S_i

	0	1	0	1
	1	0	1	0

Минимизацию булевого уравнения для сигнала суммы S_i произвести невозможно.

Карта Карно для p_i

	0	0	1	0
	0	1	1	1

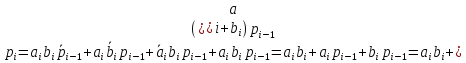
2. Двухразрядный параллельный сумматор - вычитатель в базисе И-НЕ

Преобразуем логическую функцию S_i в базис И,НЕ, применив аксиомы алгебры логики:

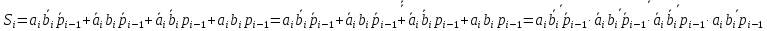
Для построения параллельного 2-разрядного сумматора необходимо взять 2 полных одноразрядных сумматора (или 2 формирователя сигнала суммы) и дополнительно создать блок формирователя сигнала переноса по следующим булевым уравнениям:

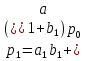
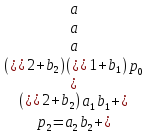
Сумматор-вычитатель работает по принципу сложения уменьшаемого в прямом коде и вычитаемого в обратном коде. Для получения вычитаемого в обратном коде используют логическую функцию ИСКЛ ИЛИ и на вход первого разряда подают сигнал переноса:

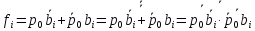
Логическая схема 2-разрядного параллельного сумматора-вычитателя, построенная в базисе И-НЕ

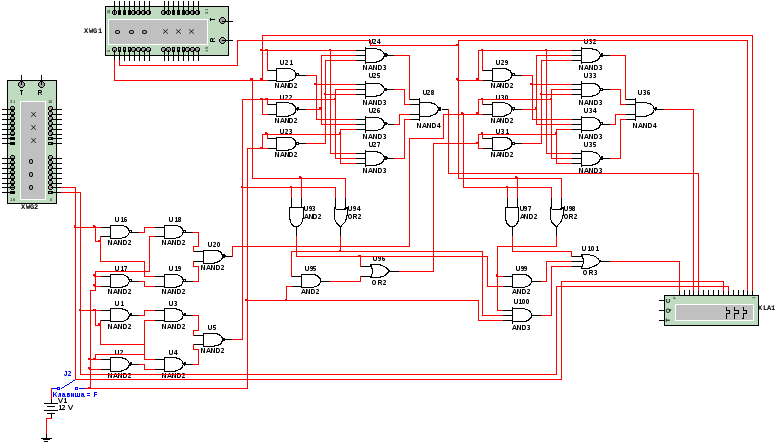
Осцилограмма сигналов параллельного 2-разрядного сумматора в режиме суммирования (ключ разомкнут)

Осцилограмма сигналов параллельного 4-разрядного сумматора в режиме вычитания (ключ замкнут)

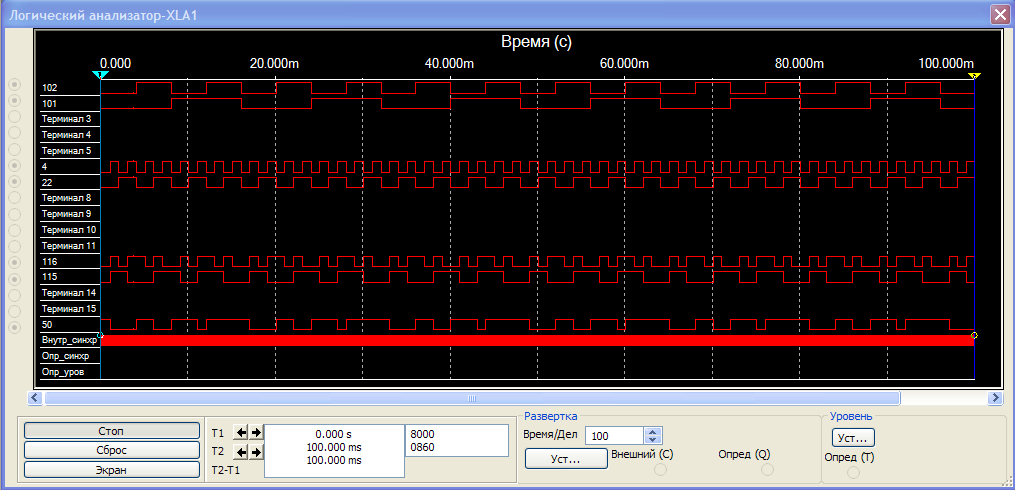
Проверим работу сумматора в режиме сложения:

10+01=0 11

11+01=1 00

Проверим работу сумматора в режиме вычитания:

11-01=11+11=1 10

11-11=11+01=1 00

Вывод

В данной работе проведены моделирования логической схемы полного одноразрядного сумматора и логической схемы 2-разрядного параллельного сумматора-вычитателя.

В результат2 мы получили осциллограммы входных и выходных сигналов и составили таблицу истинности одноразрядного сумматора. Полученная таблица истинности совпадает с той частью исходной таблицы истинности сумматора, на которой p_i-1=0.

Также были мы получили осциллограммы работы 2-разрядного параллельного сумматора в режимах суммирования и вычитания. К сожалению, полностью проверить корректность работы логической схемы на всех наборах данных не удалось, поэтому были взяты произвольные участки осциллограмм и проверены полученные значения, которые оказались корректными. Также можно заметить, что на данных осциллограммах представлены не все возможные сочетания чисел A и B.

В результате моделирования можно придти к выводу о том, что максимальное быстродействие параллельных сумматоров достигается за счёт дополнительных аппаратных и мощностных затрат, что делает такие сумматоры невыгодными и поэтому на практике лучше использовать параллельно-последовательные сумматоры.