- •Кафедра математических методов в экономике Линейная алгебра
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Линейная алгебра (2 семестр)
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
Министерство образования и науки Российской Федерации
ФГБОУ ВПО «Магнитогорский государственный
технический университет им. Г.И. Носова»
Кафедра математических методов в экономике Линейная алгебра
Варианты заданий к контрольной работе № 2 по дисциплине «Линейная алгебра» для студентов заочного факультета направления 080100 «Экономика»
Магнитогорск 2012
Вариант 1
Привести уравнение кривой
 к каноническому виду и построить кривую. Найти фокусы,
вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).
к каноническому виду и построить кривую. Найти фокусы,
вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).Даны векторы
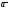 =(7,
4, 2),
=(7,
4, 2), =(5,
0, 3),
=(5,
0, 3),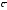 =(0,
11, 4),
=(0,
11, 4), =(-17,
-29, -4). Показать, что векторы
=(-17,
-29, -4). Показать, что векторы ,
,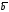 ,
, образуют базис трехмерного пространстваR3и найти координаты
вектора
образуют базис трехмерного пространстваR3и найти координаты
вектора в этом базисе.
в этом базисе.Пусть в пространстве
 дан базис
дан базис и
и
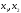 - координаты произвольного вектора
- координаты произвольного вектора относительно данного базиса, а также
задан оператор
относительно данного базиса, а также
задан оператор
A =
-2
=
-2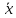 .
.
Установить, что данный оператор является
линейным, найти его матрицу относительно
базиса
 и выяснить геометрический смысл
оператора.
и выяснить геометрический смысл
оператора.
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей А:
А= .
.
Задана матрица А линейного оператора относительно базиса
 ,
, ,
,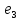 .
Найти матрицу данного оператора
относительно базиса
.
Найти матрицу данного оператора
относительно базиса  ,
,
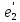 ,
, .
.
|
А= |
|
|
| |
|
| |
|
|
|
Имеется nотраслей промышленности, каждая из которых производит свою продукцию. Часть ее идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другаяY(конечный продукт) предназначена для личного и общественного потребления. Пусть
 – общий (валовой) объем продукцииi–й отрасли (
– общий (валовой) объем продукцииi–й отрасли ( );
); объем продукцииi–й
отрасли, потребляемойj–й отраслью в процессе производства
(
объем продукцииi–й
отрасли, потребляемойj–й отраслью в процессе производства
( ).
).
В таблице задан баланс nотраслей промышленности за некоторый промежуток времени.
Построить матрицу прямых затрат A=( )m×n,
где
)m×n,
где коэффициенты прямыхзатрат(доли продукцииi–й
отрасли, идущих на производство единицы
продукцииj–й
отрасли) и выяснить, является ли
она продуктивной. Найти матрицу полных
затрат. Найти
коэффициенты прямыхзатрат(доли продукцииi–й
отрасли, идущих на производство единицы
продукцииj–й
отрасли) и выяснить, является ли
она продуктивной. Найти матрицу полных
затрат. Найти – объем валовой продукции каждой
отрасли, если конечный продукт должен
быть
– объем валовой продукции каждой
отрасли, если конечный продукт должен
быть .
Указать необходимый процент увеличения
валовой продукции по каждой отрасли.
.
Указать необходимый процент увеличения
валовой продукции по каждой отрасли.
|
Отрасли |
Потребление |
Валовой выпуск Х |
Конечный продукт
| |||
|
1 |
2 |
3 | ||||
|
1 |
5 |
10 |
15 |
100 |
60 | |
|
2 |
10 |
10 |
20 |
100 |
80 | |
|
3 |
15 |
5 |
10 |
50 |
30 | |
Вариант 2
Привести уравнение кривой

 к каноническому виду и построить кривую. Найти фокусы,
вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).
к каноническому виду и построить кривую. Найти фокусы,
вершины линий,
эксцентриситет, уравнения директрис
и асимптот (если они есть).Даны векторы
 =(3,
2, 1),
=(3,
2, 1),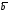 =(4,
-1, 5),
=(4,
-1, 5), =(2,
-3, 1),
=(2,
-3, 1), =(3,
-11, 2). Показать, что векторы
=(3,
-11, 2). Показать, что векторы ,
,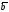 ,
, образуют базис трехмерного пространстваR3и найти координаты
вектора
образуют базис трехмерного пространстваR3и найти координаты
вектора в этом базисе.
в этом базисе.Пусть в пространстве
 дан базис
дан базис и
и
 ,
, - координаты произвольного вектора
- координаты произвольного вектора относительно данного базиса, а также
задан оператор
относительно данного базиса, а также
задан оператор
A =
= .
.
Установить, что данный оператор является
линейным, найти его матрицу относительно
базиса и выяснить геометрический смысл
оператора.
и выяснить геометрический смысл
оператора.
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей А:
А= .
.
Задана матрица А линейного оператора относительно базиса
 ,
,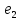 ,
,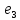 .
Найти матрицу данного оператора
относительно базиса
.
Найти матрицу данного оператора
относительно базиса  ,
,
 ,
, .
.
|
А= |
|
|
| |
|
|
Имеется nотраслей промышленности, каждая из которых производит свою продукцию. Часть ее идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другаяY(конечный продукт) предназначена для личного и общественного потребления. Пусть
 – общий (валовой) объем продукцииi–й отрасли (
– общий (валовой) объем продукцииi–й отрасли ( );
); объем продукцииi–й
отрасли, потребляемойj–й отраслью в процессе производства
(
объем продукцииi–й
отрасли, потребляемойj–й отраслью в процессе производства
( ).
).
В таблице задан баланс nотраслей промышленности за некоторый промежуток времени.
Построить матрицу прямых затрат A=( )m×n,
где
)m×n,
где коэффициенты прямыхзатрат(доли продукцииi–й
отрасли, идущих на производство единицы
продукцииj–й
отрасли) и выяснить, является ли
она продуктивной. Найти матрицу полных
затрат. Найти
коэффициенты прямыхзатрат(доли продукцииi–й
отрасли, идущих на производство единицы
продукцииj–й
отрасли) и выяснить, является ли
она продуктивной. Найти матрицу полных
затрат. Найти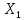 – объем валовой продукции каждой
отрасли, если конечный продукт должен
быть
– объем валовой продукции каждой
отрасли, если конечный продукт должен
быть .
Указать необходимый процент увеличения
валовой продукции по каждой отрасли.
.
Указать необходимый процент увеличения
валовой продукции по каждой отрасли.
|
Отрасли |
Потребление |
Валовой выпуск Х |
Конечный продукт
| |||
|
1 |
2 |
3 | ||||
|
1 |
10 |
10 |
25 |
100 |
70 | |
|
2 |
15 |
15 |
10 |
50 |
20 | |
|
3 |
20 |
15 |
15 |
100 |
50 | |

 ;
;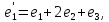
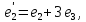


 ;
;