Расчет переходных процессов по возмущающему воздействию

Переходная функция системы при единичном возмущающем воздействии, когда выходной величиной является выходная величина внешнего контура и на выходе системы имеется установившийся процесс с y₂=1.

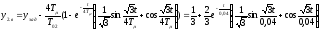
Для упрощенного случая

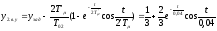
где T’_μ=2T_μ=0,04с.

Переходная функция системы при возмущающем воздействии, когда выходной величиной является выходная величина внутреннего контура, будет оптимальной

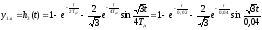
Для упрощенной САР

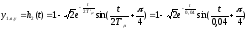
где T’_μ=2T_μ=0,02.

Подставляя значения времени, строим кривые переходных процессов при возмущающем воздействии. Построение кривых переходного процесса представлен на рисунке 3.4. Построение начнем с момента времени 30T_μ=0,3c. До этого времени используем построение кривых при управляющем воздействии.

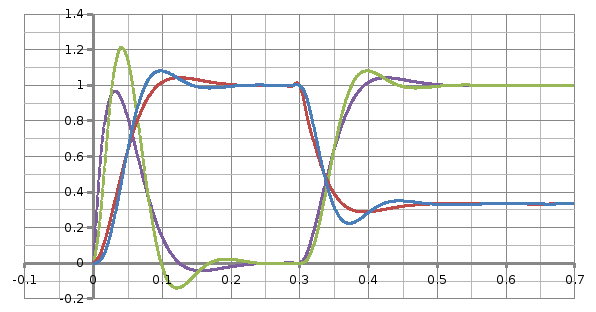
Рисунок 3.4 - Кривые переходного процесса при возмущающем воздействии

3.4 Расчёт и построение переходных процессов статической сар по управляющему и возмущающему воздействиям по методу структурного моделирования

Используя программу Matlab проведем моделирование переходных процессов.

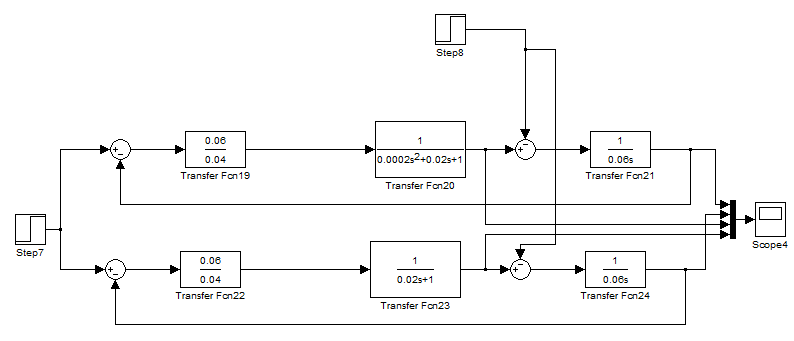
Рисунок 3.5 – Схема моделирования

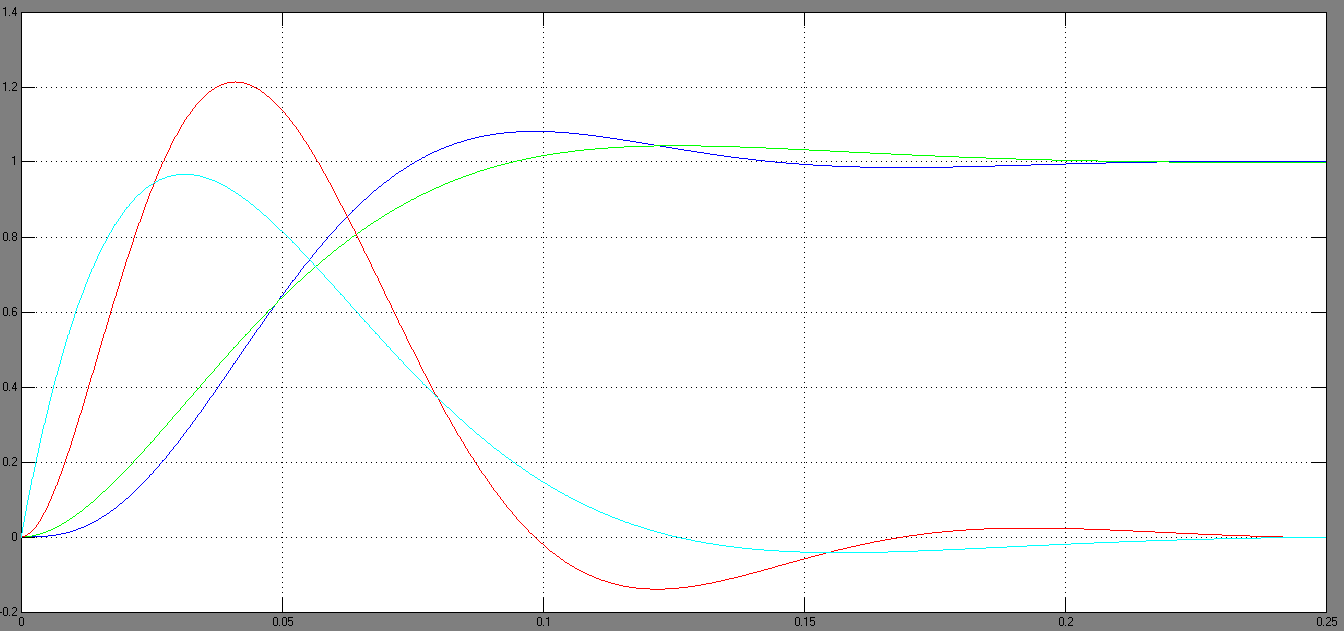
Рисунок 3.6 - Кривые переходных процессов САР по управляющему воздействию

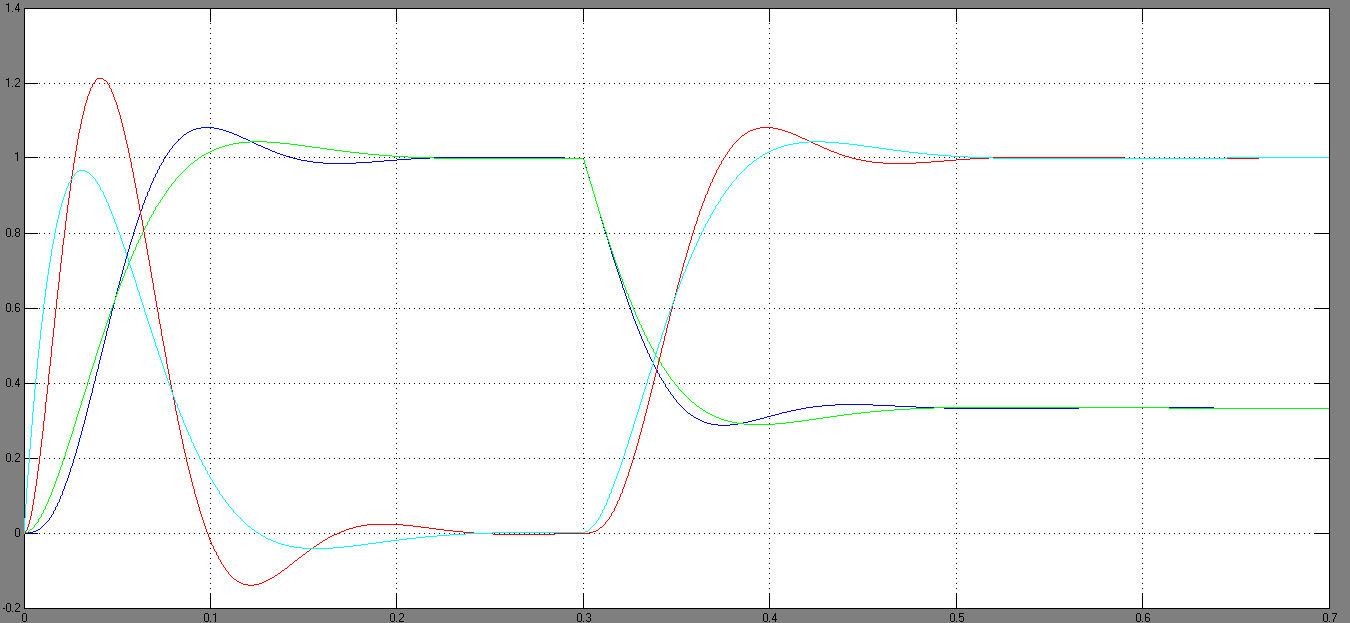
Рисунок 3.6 - Кривые переходных процессов САР по возмущающему воздействию

3.5 Определение показателей качества статических сар

При управляющем воздействии

Перерегулирование САР

Перерегулирование упрощённой САР

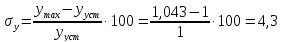
Время, когда выходная координата входит в 5% значение и больше не выходит

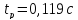
Время, когда выходная координата входит в 5% значение и больше не выходит для упрощённой САР

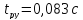
Время, когда в первый раз достигается установившийся режим

Время, когда в первый раз достигается установившийся режим для упрощённой САР

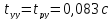
Время достижения максимального значения

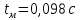
Время достижения максимального значения для упрощённой САР

Статическая ошибка САР

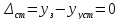
При возмущающем воздействии

Статическая ошибка САР

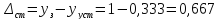
Система астатическая по управляющему воздействию и астатическая по возмущающему

4 Расчет и исследование двухконтурной астатической сар с последовательной коррекцией

4.1 Структурная схема сар, настроенной по симметричному оптимуму. Расчёт регулятора вешнего контура

Из способа оптимизации по техническому оптимуму следует, что для получения астатической характеристики в контуре регулирования надо вводить в систему регулятор с интегрирующей составляющей. Если интегрирующая составляющая отсутствует, то система будет статической. На нашу систему действует как управляющее, так и возмущающее воздействие. Внутренний контур регулирования содержит в регуляторе интегрирующее звено, и система является астатической по управляющему воздействию. Однако в нашей двухконтурной системе, рассмотренной в п.3, регулятор - пропорциональное звено, поэтому возмущающее воздействие приводит к появлению статической ошибки.

Часто на практике требуется получение системы астатической и по управлению, и по возмущению, где статическая ошибка отсутствует полностью. Для этого в систему необходимо ввести второе интегрирующее звено - регулятор с интегральной составляющей. При этом система станет как астатической (по управляющему воздействию и по возмущающему воздействию), так и неустойчивой, потому что ЛАЧХ будет пересекать ось абсцисс с наклоном - 40 дБ/дек, что является признаком неустойчивости. В этом случае необходимо изменить ЛАЧХ системы таким образом, чтобы частота среза соответствовала участку ЛАЧХ с наклоном - 20 дБ/дек. Переход с - 40 дБ/дек на - 20 дБ/дек должен происходить на октаву раньше, следовательно, получаем характеристику, которая будет симметрична относительно частоты среза. Такая система будет устойчивой. Закон такой оптимизации назван симметричным оптимумом по виду желаемой ЛАЧХ. Система, оптимизированная по такому оптимуму - система с двукратным интегрированием, астатическая по возмущающему и управляющему воздействию. ЛАЧХ такой системы представлена на рисунке 4.1.

Передаточная функция системы построенной по симметричному оптимуму

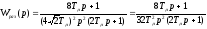
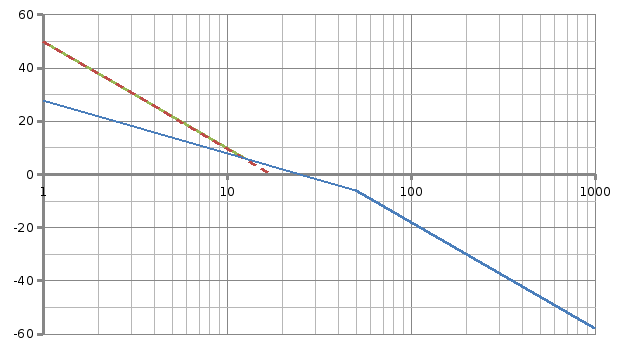
Рисунок 4.1 - ЛАЧХ системы, построенной по симметричному оптимуму

Показатели такой схемы:

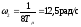
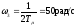
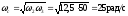
Максимальный запас по фазе наблюдается при частоте среза 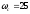рад/с.

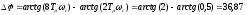
Перерегулирование системы при частоте среза

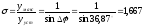
При исследовании системы, оптимизированной по симметричному оптимуму, будем представлять внутренний контур как апериодическое звено первого порядка с постоянной регулирования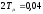с, т.е. по упрощенной схеме САР.

Для определения регулятора необходимо из желаемой ЛАЧХ вычесть ЛАЧХ разомкнутого внешнего контура, настроенного на технический оптимум.

В итоге получим ЛАЧХ, представленную на рисунке 4.2.

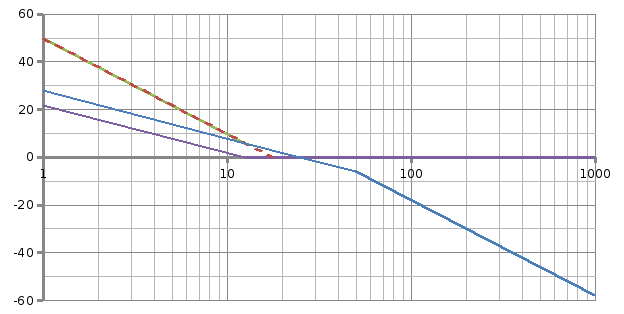
Рисунок 4.2 – ЛАЧХ регулятора

ЛАЧХ соответствует ПИ звену с передаточной функцией

Рисунок 4.3 - Структурная схема системы, настроенной на симметричный оптимум

Для уменьшения перерегулирования при управляющем воздействии в такой системе перед входом ставят фильтр с передаточной функцией

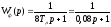
В соответствии с этими положениями строим структурную схему САР представленную на рисунке 4.4.

Рисунок 4.4 - Структурная схема САР, оптимизированной по симметричному оптимуму