Билет №41

Б И Л Е Т № 41

1. Переходные процессы в электроприводах с линейными механическими характеристиками без учета индуктивности.

2. Ограничение ускорения в системе подчиненного регулирования координат с ПИ-регулятором скорости, динамические характеристики.

3. Сравнительный анализ преобразователей частоты комплектных электроприводов.

1. Переходные процессы в электроприводах с линейными механическими характеристиками без учета индуктивности.

Переходный процесс электропривода с линейной механической характеристикой при одно и многоступенчатом пуске в случае М_с=const; ₀=const

При одноступенчатом пуске переходный процесс описывается уравнениями

;

если увеличение скорости происходит не от =0, а от какого-то начального установившегося значения, как показано на графиках. Закон изменения ускорения

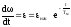, где

Уменьшение по мере увеличения скорости объясняется непрерывным уменьшением динамического момента М_дин. Если разгон идет из неподвижного состояния, т.е. когда _нач=0 , то

Время разгона на любом участке процесса до какой либо промежуточной скорости _кон

Т.к. _кон=_c , то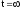 . Практически процесс считается закончившимся, когда разность между установившимся и текущим значением снижается до 2%, т.е.

или

При _нач=0 _кон=0,98_с . поэтому

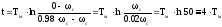
Обычно принимается t=(3-4)T_м

Величину Т_м можно определить проведя касательную в любой точке кривой (t) или М(t), например, в начале координат, как показано на графиках или используя следующие выражения

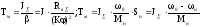
Для расчета переходного процесса при многоступенчатом пуске сначала строится пусковая диаграмма по ранее изложенным правилам задавшись пусковым и переключающим моментами. Для любой ступени разгона время, в течение которого момент изменяется от М₁ до М₂ может быть определено по формуле

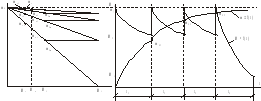
Постоянная времени для любой ступени разгона

Законы изменения и М при разгоне на любой ступени определяются согласно ранее приведенным выражениям.

Для примера рассчитаем переходный процесс на первой и второй ступенях. Сначала для первой ступени

1. 3.

2. 4.

Значения _н1 и _с1 находятся из графика, где изображена пусковая диаграмма при М=М_н и М=М_с . Задаваясь временем t от 0 до t₁ , рассчитываются законы изменения и М на первой ступени и строятся кривые =f(t) и M=f(t).

Далее делается расчет процесса на второй ступени

1. 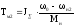3.

2. 4.

Значения _с2 и _к1 находятся из пусковой диаграммы. Задавясь временем t от 0 до t₂, рассчитываются и строятся кривые =f(t) и M=f(t) для второй ступени и т.д. Время разгона на естественной характеристике до _н=_с принимается равным t_н=(3-4)T_м, где в Т_м вместо _нх подставляется _н.

Переходные процессы электропривода с линейной механической характеристикой при М_с=const, ₀=const в тормозных режимах

Рассмотрим сначала реверс, который заключается в торможении противовключением с дальнейшим изменением направления вращения и разгоне в противоположную сторону.

Если реверс осуществляется при активном моменте сопротивления М_с=const, переходный процесс описывается уравнениями, приведенными ранее для двигательного режима, с той разницей, что в выражениях для и М нужно поставить знак минус перед _с и перед М_нач

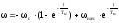
На графике с механическими характеристиками показан переход из двигательного режима в режим противовключения и построены кривые переходного процесса. Двигатель при переводе его в режим противовключения тормозится по линии ВС. Затем, если его не отключить от сети, будет разгоняться в обратном направлении по линии CD, достигает скорости идеального холостого хода (-₀) и т.к. момент сопротивления активный, переходит в генераторный режим с отдачей энергии в сеть (линия DE). Равновесие наступит в т.Е, где М=М_с и скорость _с .Такой процесс может быть, если в случае подъема тяжелого груза двигатель тормозится противовключением и при =0 не отключается и не затормаживается механическими тормозами.

При реактивном моменте сопротивления процесс разбивается на два этапа. На первом этапе, являющемся тормозным, законы изменения и М описываются теми же уравнениями что и при активном М_c. Время торможения до 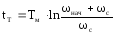 , где - _с- фиктивная скорость, к которой стремиться двигатель.

На втором этапе происходит разгон в противоположном направлении (после торможения противовключением и остановки). Знак М_с меняется на противоположный. Уравнения, описывающие переходный процесс будут иметь такой же вид, как для пуска двигателя, только _нач нужно принять равной 0, М_нач=-М_п и _с=-_с`,т.е.

;

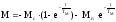
Здесь М_п- пусковой момент.

Время реверса . При переходе скорости через 0 динамический момент М_дин скачком изменяется от значения М_дин=-(М_п+М_с) до М_дин=-(М_п-М_с) , что вызывает соответствующее изменение ускорения и в кривых =f(t) и M=f(t) появляется излом.

При динамическом торможении законы изменения и М описываются теми же уравнениями, что и для реверса, т.е.

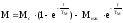; , где _с- установившаяся

скорость, определяемая точкой пересечения механической характеристики динамического торможения и вертикали М_c =const.

В случае активного М_с точка “B”, соответствующая установившейся скорости _с2, относится к случаю, когда этот момент в начале процесса является тормозным, что имеет место, например, при подъеме груза, а т. “c” с установившейся скоростью _с1- к случаю, когда этот момент является движущим, например, при спуске груза (рис.а).

В случае торможения при подъеме груза под действием М_с и тормозного момента двигателя привод вначале будет тормозится и остановится, т.к. момент двигателя станет равным 0, но т.к. М_с является активным и будет продолжать действовать в том же направлении, под его действием система будет вращаться в обратную сторону. При этом М_с из момента сопротивления (тормозного) превратится в движущий, а тормозной момент двигателя изменит свой знак и будет продолжать действовать как тормозной. Установившаяся скорость наступит при равенстве момента двигателя и М_с т.е. в т. В. Кривые переходного процесса для этого случая изображены на рис. “б”. Время торможения до 0 , т.е. до остановки

Если активный момент сопротивления в начале торможения был движущим (торможение при спуске груза ), то в начале торможения тормозной момент двигателя (отрезок ED на рис.”а”) больше движущего статического момента и имеет место замедление, сопровождающееся уменьшением тормозного момента двигателя. При скорости _с1 M=M_c, замедление прекращается и наступает установившийся режим тормозного спуска груза со скоростью _с1. В этом случае затормозить систему до остановки путем динамического торможения нельзя (рис.”в”).

При реактивном моменте сопротивления динамическое торможение происходит так же, как и при подъеме груза. Разница лишь в том, что при =0 действие реактивного М_с прекратится, и т.к. момент двигателя тоже станет равным 0, система остановится. Соответствующие этому случаю механические характеристики и кривые =f(t) и М=f(t) изображены на приведенных рис. Процесс будет протекать так, как если бы скорость  стремилась стать равной-_с , но прекратится при =0. Поэтому соответствующие отрезки кривых на графике изображены пунктиром.

В заключение следует отметить, что процессы пуска и торможения в электроприводах, получающих питание от сети ( =const) отличаются от оптимальных.

Переходные процессы электропривода с линейной механической характеристикой при М_с=f()

В случае линейной М от , т.е. при М_с=к дифференциальное уравнение, определяющее переходный процесс, имеет вид

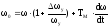, где

_y- скорость установившегося режима при М_с=М_y ,

_y- падение скорости при установившемся режиме .

Учитывая, что _y+_y=₀ и умножая обе части уравнения на 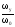, получим

откуда 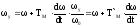,где

Решение этого уравнения относительно и М дает законы изменения  , М и I

;

Длительность переходного процесса

Т`_м- это время, за которое электропривод разгонится из неподвижного состояния до _y при постоянном М_пуск.

При М_с=М₀+К₁(рис.”a”) и М_с=М₀-К₁(рис.”б”) переходный процесс описывается этими же уравнениями, что и при М_с=К, но в них

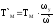
При вентиляторном моменте сопротивления дифференциальное уравнение, отражающее переходный процесс, имеет вид

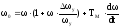
Хотя это уравнение решить можно, однако конечные результаты мало пригодны для практического использования.Поэтому на практике чаще используются графические и графоаналитические методы. Естественно, что такие методы дают лишь приближенные результаты, однако, при тщательном выполнении их точность достаточна для решения практических задач. Правда, такие методы имеют и такой недостаток: они не дают возможности получить общие выводы. Решение может быть найдено лишь для отдельных частных случаев, когда значения всех параметров электропривода известны. Рассмотрим некоторые из них.

2. Ограничение ускорения в системе подчиненного регулирования координат с ПИ-регулятором скорости, динамические характеристики.

Структурная схема системы с ПИ-регулятором скорости представлена на рис. 23.1. ПИ- регулятор момента с коэффициентом передачи К_п1 и временем изодрома Т_и1 представлен на рис.23.1 детализированной структурной схемой. Аналогично представлен ПИ-регулятор скорости с коэффициентом передачи К_п2 и временем изодрома Т_и2 Через eps₁ и eps₂ обозначены ошибки соответственно на входах контуров регулирования момента и скорости. Выходное напряжение u_зад(м) регулятора скорости является задающим для подчиненного контура регулирования момента.

Математическая модель системы содержит 5 уравнений состояния

T_пр dw₀/dt= - w₀ +K_пр u_у

T_э = bw₀ - M- bw₁,

J_S = M- M_c

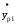= eps₁

= eps₂,

где к известным переменным состояния, характеризующим энергети-ческую подсистему ЭМС, добавлены выходы интеграторов ПИ-регу-ляторов y_p1 и y_{p2 ,} , характеризующие состояние информационной подсистемы.

Статические и динамические характеристики контура с такими настройками относительно задающего (управляющего) воздействия соответствуют характеристикам стандартной системы, настроенной на симметричный оптимум. Передаточная функция замкнутого контура по управлению имеет вид

,

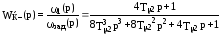или

.

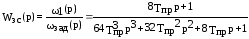При этом

а) Контур не имеет статической и скоростной ошибки, относительно сигнала задания (система обладает астатизмом второго порядка по управлению). В литературе часто такую систему называют двукратно-интегрирующей.

б) Время переходного процесса по управлению составляет величину

t_п @ 12Т_m2 @ 24Т_m1 @ 24Т_пр ,

однозначно определяется величиной постоянной времени управляемого электрического преобразователя и в 4 раза превышает время переходного процесса в контуре регулирования момента.

в) Перерегулирование при отработке скачка задания контуром, настроенным на симметричный оптимум, составляет, как известно, величину 43%. Для уменьшения его до величины 8.3% на входе контура, в канале формирования сигнала задания устанавливается фильтр в виде апериодического звена с передаточной функцией

W_ф(p)=u_зад (p)/ u_вх(p)= 1/ (Т_фp +1),

причем постоянная времени фильтра выбирается из условия компенсации числителя передаточной функции замкнутой системы, т.е.

Т_ф= 4 Т_m2 @ 8Т_m1 @ 8Т_пр.

Для учета такого фильтра математическую модель системы следует дополнить еще одним уравнением

Рассмотрим далее характеристики контура относительно возму-щающего воздействия (момента нагрузки М_с)

Преобразуя схему известным образом, получим

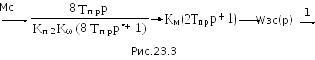
w₁

Передаточная функция системы по возмущению

W_в(p)=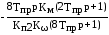

или с учетом выражения для коэффициента передачи ПИ-регулятора оптимизированного контура

К_п2 = К_мТ_м b/ К_w4Т_пр

W_в(p)=

Найдем операторное изображение ошибки контура Dw(p) в виде изменения скорости, обусловленного скачкообразным приложением момента статической нагрузки при нулевом задании по скорости и нулевых начальных условиях

Dw(p) =

Находя установившееся значение ошибки в системе как

,

установим, что эта ошибка равна нулю при любом моменте нагрузки М_с , и следовательно, в пределах зоны пропорциональности УПП механические характеристики определяются выражением

w₁=w_зад

и по форме не отличаются от аналогичных характеристик одноконтурной системы регулирования скорости с ПИ-регулятором.

Для оценки характера процесса парирования скачкообразного возмущения определим переходную характеристику системы по возмущению, используя операторное изображение ошибки

Dw(t) =

Корни полинома знаменателя выражения, заключенного в фигурные скобки, известны:

p₁= -1/ 2T_m2=-1/4T_пр;

p_2,3= -1/ 4T_m2 ±jÖ3/ 4T_m2=-1/ 8T_пр ±jÖ3/ 8T_пр

Используя формулу разложения, находим

(23.1)

График полученной зависимости представлен на рис. 23. 4.

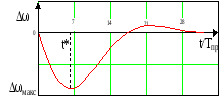
Рис. 23. 4

Анализ ее показывает, что время парирования возмущения равно времени переходного процесса по управлению, т.е. t_п @24 Т_пр и вдвое превышает время парирования возмущения в ранее рассмотренной системе с П-регулятором и настройкой на технический оптимум

Для приближенной оценки максимального значения динамического отклонения скорости Dw_макс заметим, что оно имеет место в момент времени t*@6 Т_пр. Подставляя значение t* в формулу 23.1, получим

Dw_макс@ Dw(t*)@ 3.54 (М_с/J) Т_пр

Настройка контура регулирования скорости на симметричный оптимум широко используется на практике в связи с простотой технической реализации и наличием астатизма первого порядка по возмущению. Однако, как было установлено, перерегулирование при реакции на скачок управляющего воздействия в 10 раз больше , чем в системе , с контуром скорости, настроенным на технический оптимум. Снижение величины перерегулирования без использования входного сглаживающего фильтра и при сохранении астатизма по моменту нагрузки. свойственного двукратноинтегрирующей системе, возможно в трехконтурной системе регулирования скорости.

3. Сравнительный анализ преобразователей частоты комплектных электроприводов.

На мировом рынке преобразовательной техники выделились следующие фирмы-лидеры: SIMENS, Shneider Electrique, Control Technique, ABB, Lenze которые выпускают КЭП переменного тока. Каждое новое поколение преобразователей частоты содержит всё большее число функций, как управляющих двигателем, так и улучшающих технологический процесс. В основном это функции:

— обеспечения необходимых тахограмм разгона и торможения;

— регулирование скорости в установившемся режиме;

— прецизионные задания скорости и ускорения;

— обеспечение реверса;

— автонастройки преобразователя;

— обработка сигналов обратных связей, заводимых в систему управления;

— организация контуров управления;

— защиты преобразователя от токовой перегрузки;

— реализация алгоритмов энергосбережения;

— реализация различных принципов управления (частотно-токовое, векторное, прямое управление моментом);

— визуализации сигналов;

— интеграции преобразователя в систему управления более высокого уровня (промышленную сеть);

— специальные технологические функции;

За счёт применения указанных функций, встроенных в современный КЭП, преобразователи фирмы Shneider Electrique нашли применение в следующих электроприводах:

— насосные агрегаты современных систем отопления (Altivar 21);

— системы вентиляции зданий и сооружений (Altivar 21);

— подъёмно-транспортное оборудование (Altivar 71);

— лифты (Altivar 71);

— фасовочно-упаковочное оборудование (Altivar 71);

— текстильные машины (Altivar 71);

Преобразователи фирмы Control Technique:

— металлургическая промышленность (Unidrive SP);

— крановые механизмы (Unidrive SP);

— лифты (Unidrive SP);

— насосы и вентиляторы (Commander SK);

— конвейеры (Commander SK);

— мешалки (Commander SK);

Как видно из назначения моделей разработанных и широко внедряемых КЭП, фирма-производитель выпускает КЭП ориентированно к группе или нескольким группам механизмов. Проблема унификации КЭП продолжает решаться. Однако унификация КЭП несёт и его удорожание с повышением стоимости, как силовой части, так и системы управления, увеличение габаритных размеров.

Таким образом, современная преобразовательная приводная техника, делает огромные шаги в своём развитии, постоянно совершенствуясь и тем самым повышая качество технологических процессов. Особенно важным при этом становится выработка новых подходов к её разработке и проектированию, с привлечением мощнейших вычислительных средств. Для постоянного совершенствования, необходимы научные исследования и обоснованные принятия решений, устраняющих возникающие проблемы.