
Графики в MathCAD
.docПрактическая работа № 2 Построение графиков в MathCAD
1. Построить график параметрически заданной функции при значениях конcтант а, b, . Оси графика – х и y, которые зависят от аргумента t или .
2. Сравнить график с построенным графиком в электронной таблице Excel
1
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Циклоида
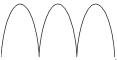
x = a(t - sin t)
y = a(1 - cos t)
t 0 6
Шаг 0,5
a = 1.25
2
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Циклоида

x = a(t - sin t)
y = a(1 - cos t)
t 0 6
Шаг 0,5
a = 2
= 2
3
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Трохоида

x = at - bsin t
y = a - bcos t
t 0 10
Шаг 0,1
a =-1
b =3
4
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Эпитрохоида

x = acos (сt) - bcos (t + сt)
y = asin (сt) - bsin (t + сt)
t 0 10
Шаг 0,5
a =3
b=2
c=0,25
5
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Гипотрохоида

x = acos (сt) - bcos (t - сt)
y = asin (сt) - bsin (t - сt)
t 0 10
Шаг 0,5
a =3
b=2
c=0,25
6
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Декартов лист

x = at / (1 + t3)
y = a t2 / (1 + t3)
t -6 6
t -1
шаг 0.2
a = 1; 2; 3; 4; 5; 6
7
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Циссоида Диоклеса

x = a t2 / (1 + t2)
y = a t3 / (1 + t2)
t -6 6
a = 1
8
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Строфоида

x = a (t2 - 1) / (t2 + 1)
y = at(t2 - 1) / (t2 + 1)
t -6 6
a = 2
9
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
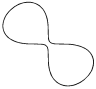
Конхоида
Никомеда

x = a + bcos t
y = atg t + bsin t
t 0 10
t /2
Шаг 0,01
a = 2
b = 1; 10; 30; 50; 90
10
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Улитка Паскаля

x = acos2 t + bcos t
y = a cos t sin t + bsin t
t 0 2
шаг 0,1
a = 4
b = 3
11
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Эпициклоида

x = (a + b)cos - acos[(a + b)/a]
y = (a + b) sin - a sin[(a + b)/a]
0 2 шаг 0,1
a = 1
b = 6
12
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Эпициклоида

x = (a + b)cos - acos[(a + b)/a]
y = (a + b) sin - a sin[(a + b)/a]
0 10
Шаг 0,2
a = 3; b = 4
= 1
13
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Эпициклоида

x = (a + b)cos - acos[(a + b)/a]
y = (a + b) sin - a sin[(a + b)/a]
0 2
Шаг 0,1
a = 1; b = 4
= 1.5
14
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Эпициклоида

x = (a + b)cos - acos[(a + b)/a]
y = (a + b) sin - a sin[(a + b)/a]
0 2
Шаг 0,1
a = 7; b = 4
= 4
15
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Гипоциклоида

x = (b - a)cos - acos[(b - a)/a]
y = (b - a) sin - a sin[(b - a)/a]
-2 2
Шаг 0,1
a = 1
b = 2.5
16
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Гипоциклоида

x = (b - a)cos - acos[(b - a)/a]
y = (b - a) sin - a sin[(b - a)/a]
0 6
Шаг 0,5
a =2.5;
b = 1
17
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Гипоциклоида

x = (b - a)cos - acos[(b - a)/a]
y = (b - a) sin - a sin[(b - a)/a]
0 2
Шаг 0,1
a = 1; b = 4
= 3
18
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Гипоциклоида

x = (b - a)cos - acos[(b - a)/a]
y = (b - a) sin - a sin[(b - a)/a]
0 10
Шаг 0,2
a = 5; b = 2
= 0.7
19
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Спираль

x = atcos t
y = btsin t
t 0 10
Шаг 0.5
a = 2
b = 2
20
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Гиперболич. спираль

x = (acos t) / t
y = (b sin t) / t
t -6 6
t 0
Шаг 0,1
a =2
b =1
21
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Гиперболич. спираль

x = (acos t) / t
y = (b sin t) / t
t 0.5 20
Шаг 0.5
a = 3
b = 1
22
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Астроида
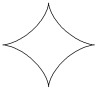
x = acos3 (t / 4)
y = b sin3 (t / 4)
t 0 8
Шаг 0.1
a = 2
b = 1
23
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Астроида
x = acos3 (t – b)
y = a sin3 t
t 0 8
Шаг 0.1
a = 2
b = 4
24
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Астроида

x = acos3 (b*t)
y = a sin3 t
t 0 8
Шаг 0.1
a = 2
b = 1.5
25
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Эвольвента

x = acos t + at sin t
y = a sin t + atcos t
t -10 10
Шаг 0,5
a =2
26
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Эвольвента

x = acos t + at sin t
y = a sin t + atcos t
t 0 20
шаг 0.5
a = -2; -1; 1; 2
27
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значения констант
Эллипс
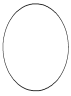
x = acos t
y = bsin t
t 0 2
Шаг 0.5
a = 7
b = 1
28
-
Название
кривой
Вид графика
Параметрические уравнения
Диапазон аргумента
Значение
константы
Эллипс

x = acos(c + t)
y = b sin(c - t)
t 0 2
Шаг 0,11
a =3
b=1
c=2
