Классификация эвм

Традиционно электронно-вычислительную технику подразделяют на аналоговую и цифровую.

В аналоговых вычислительных машинах (АВМ) обрабатываемая информация представляется соответствующими значениями аналоговых величин: тока, напряжения, угла поворота какого-либо механизма и т.п. Эти машины обеспечивают приемлемое быстродействие, но не очень высокую точность вычислений (0, 001 – 0,01). Подобные машины распространены не очень широко. Они используются в основном в проектных и научно-исследовательских учреждениях в составе различных стендов по обработке сложных образцов техники. По своему назначению их можно рассматривать как специализированные вычислительные машины

В настоящее время под термином ЭВМ обычно понимают цифровые вычислительные машины, в которых информация кодируется двоичными кодами чисел.

Практически каждое десятилетие меняется поколение машин, каждые год-два – основные типы микропроцессоров, определяющих характеристики новых ЭВМ. Поэтому любая предложенная классификация ЭВМ очень быстро устаревает и нуждается в корректировке. Например, названия мини-, миди-, и микро ЭВМ почти не используются. Однако существует ряд закономерностей развития вычислительной техники.

Академик В.М.Глушков указывал, что существует три глобальные сферы деятельности человека, которые требуют использования качественно различных типов ЭВМ:

1) традиционное направление – применение ЭВМ для автоматизации вычислений. Отличительной особенностью этого направления является наличие хорошей математической основы, заложенной развитием математических наук и их приложений.

2) вторая сфера применения ЭВМ связана с использованием их в системах управления. ЭВМ данного направления должны обеспечивать не только вычисления, но и автоматизировать сбор данных и распределение результатов обработки.

3) третье направление связано с применением ЭВМ для решения задач искусственного интеллекта. Это задачи робототехники, доказательство теорем, машинный перевод текста с одного языка на другой, планирование с учетом неполной информации, составление прогнозов, моделирование сложных процессов и явлений и т.д. Для этого направления нужны качественно новые структуры ЭВМ с большим числом вычислителей, которые обеспечивали бы параллелизм в вычислениях.

Таким образом, для решения различных задач необходима и разная вычислительная техника. Поэтому рынок компьютеров постоянно имеет широкую градацию классов и моделей ЭВМ. Так, например, фирма IBM, которая производит примерно 80% мирового машинного парка, в настоящее время выпускает в основном 4 класса компьютеров, перекрывая ими широкий класс задач пользователей.

1. большие ЭВМ (mainframe) – многопользовательские машины с центральной обработкой, с большими возможностями для работы с базами данных, с различными формами удаленного доступа.

2) машины RS/6000 − очень мощные по производительности, предназначены для построения рабочих станций для работы с графикой,UNIX-серверов, кластерных комплексов. Первоначально эти машины предполагалось применять для обеспечения научных исследований.

3) средние ЭВМ, предназначены для работы в финансовых структурах (ЭВМ типа AS/400-AdvancedPortableModel3 – «бизнес-компьютеры», 64-разрядные). В этих машинах особое внимание уделяется сохранению и безопасности данных, программной совместимости и т.п. Используются в качестве серверов локальных сетей и сетей корпораций.

4) компьютеры на платформе микросхем фирмы Intel.IBM-совместимые компьютеры этого класса составляют примерно 50% рынка всей компьютерной техники. Более половины их поступает в сферу малого бизнеса. Несмотря на столь внушительный объем выпуска компьютеров этой платформы, фирмаIBMпроводит исследования и развивает собственную альтернативную платформу, получившую названиеPowerPC.

Кроме перечисленных типов ВТ, необходимо отметить класс вычислительных систем, получивших название суперЭВМ. С развитием науки и техники постоянно выдвигаются новые крупномасштабные задачи, требующие выполнения больших объемов вычислений. Особенно эффективно применение суперЭВМ при решении задач проектирования, в которых натурные эксперименты оказываются дорогостоящими, недоступными или практически неосуществимыми. В этом случае ЭВМ позволяет методами численного моделирования получить результаты вычислительных экспериментов. Дальнейшее развитие суперЭВМ связывается с использованием направления массового параллелизма, при котором одновременно могут работать сотни и даже тысячи процессоров. Образцы таких машин уже выпускаются несколькими фирмами: nCube(гиперкубические ЭВМ),ConnectionMachine,MassPar,NCR/Teradata,KSR,IBMRS/6000,MPPи др.

На рубеже тысячелетий фирма IBMобъявила о разработке новой суперЭВМ, которая будет содержать более миллиона микропроцессоров типаPentiumIII(10²⁰), по расчетам она должна иметь быстродействие 10¹⁵операций в сек.

Необходимо отметить и еще один класс наиболее массовых средств электронно-вычислительной техники – встраиваемые микропроцессоры. Эти устройства универсальны по характеру применения – встраиваются в отдельные машины, объекты, системы.

Классификация по быстродействию:

1) суперЭВМ для решения крупномасштабных вычислительных задач, для обслуживания крупнейших информационных банков данных;

2) большие ЭВМ для комплектования ведомственных, территориальных и региональных вычислительных центров;

3) средние ЭВМ широкого назначения для управления сложными технологическими производственными процессами и могут быть использованы в качестве сетевых серверов;

4) персональные и профессиональные ЭВМ, позволяющие удовлетворять индивидуальные потребности пользователей. На их базе строятся автоматизированные рабочие места (АРМ) для специалистов различного уровня;

5) встраиваемые микропроцессоры, осуществляющие автоматизацию управления отдельными устройствами и механизмами.

С развитием сетевых технологий начинает все больше использоваться другой классификационный признак, который отражает место и роль ЭВМ в сети:

−мощные машины и вычислительные системыдля управления гигантскими сетевыми хранилищами информации (их можно отнести по своим характеристикам к классу суперЭВМ, но в отличие от них они являются более специализированными и ориентированными на обслуживание мощных потоков информации;

−кластерные структуры – многомашинные распределенные вычислительные системы, объединяющие несколько серверов, что позволяет гибко управлять ресурсами сети, обеспечивая необходимую производительность, надежность, готовность и другие характеристики;

−серверы – вычислительные машины и системы, управляющие определенными ресурсами сети. Различают файл-серверы, серверы приложений, факс-серверы, почтовые, коммуникационные,Web-серверы и др.

−рабочая станция. Термин «рабочая станция» отражает факт наличия в сетях абонентских пунктов, ориентированных на работу профессиональных пользователей с сетевыми ресурсами. Этот термин как бы отделяет их от персональных ЭВМ, обеспечивающих работу основной массы непрофессиональных пользователей, работающих обычно в автономном режиме;

−сетевые компьютеры– упрощенные персональные компьютеры, вплоть до карманных. Их основным назначением является обеспечение доступа к сетевым информационным ресурсам.

Информационно-логические основы ЭВМ

Системы счисления

Система счисления  принятый способ записи чисел и сопоставления этим записям реальных значений (это код, в котором используются специальные символы для обозначения количества каких-либо объектов). Все системы счисления можно разделить на два класса: позиционные и непозиционные.

Для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Число таких знаков в позиционной системе счисления называется основанием системы счисления. Например, общее количество символов в десятичной системе равно 10 (0, 1…..9), поэтому ее называют системой счисления с основанием 10. Примеры систем счисления приведены в табл.2.

В позиционной системе счисления число может быть представлено в виде суммы произведений коэффициентов на степени основания системы счисления [257₍₁₀₎=2×10²+5×10¹+7×10⁰]. Значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Поэтому такие системы счисления называютпозиционными.

Некоторые системы счисления

Таблица 2

Основание	Система счисления	Знаки
2	Двоичная	0,1
3	Троичная	0,1,2
4	Четвертичная	0,1,2,3
5	Пятеричная	0,1,2,3,4
8	Восьмеричная	0,1,2,3,4,5,6,7
10	Десятичная	0,1,2,3,4,5,6,7,8,9
12	Двенадцатеричная	0,1,2,3,4,5,6,7,8,9,А,В
16	Шестнадцатеричная	0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

Примеры:

23,435₍₁₀₎=2×10¹⁺3×10⁰+4×10^-1+3×10^-2 +5×10^-3

6

Степени коэффициентов целогочисла проставляютсясправа налево, адробногослева направо.

92₍₁₀₎=6×10²+9×10¹+2×10⁰

1101₍₂₎=1×2³+1×2²+0×2¹+1×2⁰

112₍₃₎=1×3²+1×3¹+2×3⁰

341,5₍₈₎=3×8²+4×8¹+1×8⁰+5×8^-1

A1F,4₍₁₆₎=A×16²+1×16¹+F×16⁰+4×16^-1

Наиболее распространенными являются двоичная, десятичная, восьмеричная и шестнадцатеричная. Поэтому большое значение имеет перевод из одной системы счисления в другую.

Правило 1. Чтобы перевести целую часть числа из десятичной системы в систему с основанием В, необходимо разделить ее на В. Остаток даст младший разряд числа. Полученное при этом частное, необходимо вновь разделить на В – остаток даст следующий разряд числа и т.д.

Кроме рассмотренных позиционных систем счисления существуют такие, в которых значение знака не зависит от того места, которое он занимает в числе. Такие системы счисления называют непозиционными. Наиболее известная среди них − римская. В этой системе используется 7 знаков [I(1),V(5),X(10),L(50),C(100),D(500),M(1000)].

Примеры: III-три,LIX-(пятьдесят девять),DLV-(пятьсот пятьдесят пять).

Двоичная система счисления.

В основе цифровой техники лежит двоичная система выражения цифр, именуемая еще бинарной, а связанный с ней математический аппарат — алгебра логики, или булева алгебра, названная так в честь Д.Буля, английского математика XIX века, основоположника математической логики.

В двоичной системе счисления удается любое число записать с помощью 1 или 0. Например, двоичное число 11101011 соответствует 235 в десятичной системе счисления. Каждая позиция числа, представляет одно из двух состояний (1 или 0).

В общем случае двоичное число имеет целую и дробную части, например, 1101101.10111.

Каждая позиция, занятая двоичной цифрой, называется бит. Битявляетсянаименьшейединицей информации в ЭВМ. Наименьшим значащим битом называют самый младший двоичный разряд (МЗР), а самым старшим двоичным разрядом - наибольший значащий бит (СЗР). В двоичном числе эти биты имеют, соответственно, наименьший и наибольший вес. Обычно двоичное число записывают так, что старший значащий бит является крайним слева.

Перевод чисел из десятичной системы счисления в двоичную производится по выше приведенному правилу 1.

Пример.

Перевести целое десятичное число 10₍₁₀₎в двоичное число.

Пример.

Десятичное число 57₍₁₀₎преобразовать в двоичное число.

Для перевода дробной части числа, ее нужно умножить на 2. Целая часть произведения будет первой цифрой числа в двоичной системе, затем, отбрасывая у результата целую часть, вновь умножаем на 2 и т.д. Нужно отметить, что конечная десятичная дробь при этом вполне может стать бесконечной (периодической) двоичной. Например.

0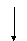,73*2=1,46 (целая часть 1)

0,46*2=0,92 (целая часть 0)

0,92*2=1,84 (целая часть 1)

0,84*2=1,68 (целая часть 1)

и т.д.

В итоге: 0,73₍₁₀₎=0,1011…₍₂₎

Из рассмотренных выше примеров видно, что если десятичное число дробное, то его преобразование в двоичное должно выполняться отдельно над его целой и дробной частью.

С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатеричных чисел.

Правило 2. Для перевода целого двоичного числа в восьмеричное, необходимо разбить его справа налево на группы по три цифры (самая левая группа может содержать менее трех двоичных цифр), затем каждой группе поставить в соответствие ее восьмеричный эквивалент (см. табл.3). Группу из трех двоичных цифр часто называют «двоичной триадой».

Пример: 11011001₂ = 11 011 001₂ = 331_8.

Двоичный, восьмеричный и шестнадцатеричный эквиваленты для десятичных чисел от 0 до 15

Таблица 3

Десятичное число	Двоичное число	Восьмеричное число	Шестнадцатеричное число
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Правило 3.Перевод целого двоичного числа в шестнадцатеричное производится путем разбиения данного числа на группы по четыре цифры«двоичные тетрады».

Пример: 1100011011001₂= 1 1000 1101 1001₂= 18D9_16.

Правило 4.Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатеричную системы счисления аналогичное разбиение на триады или тетрады производится от точки вправо (с дополнением недостающих цифр нулями).

Примеры: 0,1100011101₂= 0, 110 001 110 100₂= 0,6164₈;

0,1100011101₂= 0, 1100 0111 0100₂= 0,С74_16.

Правило 5.Перевод восьмеричных (шестнадцатеричных) чисел в двоичные, производится обратным путемсопоставлением каждому знаку числа соответствующей тройки (четверки) двоичных чисел.

Преобразования чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы и обратно столь просты (по сравнению с операциями между этими тремя системами и привычной нам десятичной системой счисления) потому, что числа 8 и 16 являются целыми степенями числа 2 (2³; 2⁴). Этой простотой и объясняется популярность восьмеричной и шестнадцатеричной систем счисления в вычислительной технике и программировании.

Примеры перевода чисел из одной позиционной системы счисления в другую сведены в таблицу-«подсказку» — схема 7, в которой в сжатой, но информационно-емкой форме представлены способы перевода из одной системы счисления в другую.

Над числами, записанными в любой системе счисления, можно производить различные арифметические операции.

Правила выполнения арифметических действий над двоичными числами определяются арифметическими действиями над одноразрядными двоичными числами.

Сложение Вычитание Умножение

перенос в старший разряд

Правила выполнения арифметических действий во всех позиционных системах счисления аналогичны.