1. Дискретная двумерная случайная величина (продолжение).

Для двумерной дискретной случайной величины вводится функция распределения по формуле и означает геометрически попадание случайной точки в левый нижний квадрант, ограниченный горизонтальной и вертикальной прямыми, проходящими через точку плоскости . Визуально график функции распределения представляет собой «угловую лестницу с разновысокими ступенями, переходящую в плато, общей высотой 1».

Свойства аналогичны свойствам обычной функции распределения дискретной случайной величины.

Свойства

1. .

2. неубывающая функция по каждому аргументу, т.е. , если и , если .

3. (хотя бы один из аргументов равен «»).

4. Если один из аргументов равен «», то становится функцией распределения для второй составляющей: , т.к. . Аналогично . Здесь и − функции распределения составляющих и двумерной случайной величины .

5. , т.к. событие − достоверное.

2. Непрерывная двумерная случайная величина

Задается функцией распределения , которая является непрерывной и имеющей вторую смешанную производную почти всюду. Эта производная обозначается и называется плотностью вероятности двумерной случайной величины. (Обратите внимание, что эта функция вводится только для непрерывных случайных величин.) График плотности вероятности − поверхность в пространстве: «гора или горы, переходящие вдали от начала координат в равнину».

Свойства

1. .

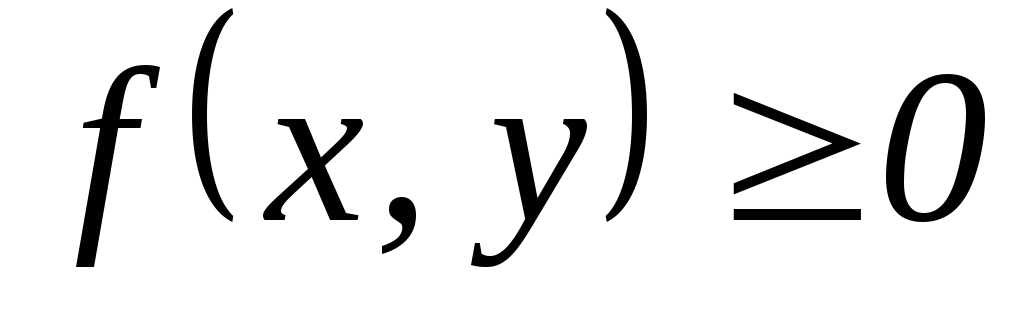2. Вероятность попадания случайной величины в область :

.

3. .

4. .

5. , т.к. ,

, т.к. .

Дифференцируя предыдущие равенства по и , получим

6. ,

или , ,

где и − плотности вероятностей составляющих и двумерной случайной величины .

§ 11. Условные законы распределения

Для дискретных величин были введены условные вероятности по формулам

и .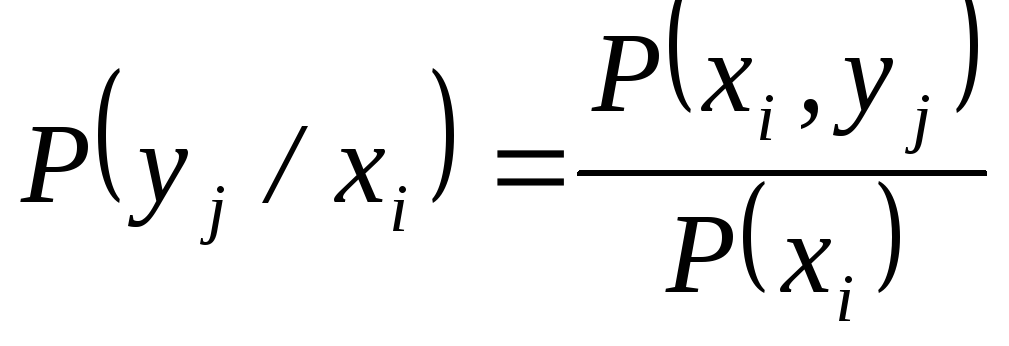

Для непрерывных величин аналогично вводятся плотности для условных законов распределения

и .

Числовые характеристики составляющих и двумерной случайной величины можно найти по формулам

,

,

,

.

Аналогичные характеристики можно ввести и для условных распределений, например, условные математические ожидания

, .

Условное математическое ожидание будет функцией от :

, (1)

и наоборот, условное математическое ожидание будет функцией от:

. (2)

Функции (1) и (2) называются функциями регрессии: (1) − на , а (2) − на . Графики этих функций называются линиями регрессии или кривыми регрессии.

§ 12. Зависимые и независимые случайные величины

Определение. Случайные величины и называются независимыми, если условные законы любой из них совпадают с безусловными:

для дискретных случайных величин

, т.е. ,

для непрерывных

, т.е. .

Таким образом, плотность вероятности совместного распределения системы равна произведению плотностей распределения составляющих. Это условие является не только необходимым, но и достаточным для непрерывных случайных величин. Точнее, имеет место следующая теорема.

Теорема (критерий независимости случайных величин). Для того, чтобы случайные величины и были независимыми необходимо и достаточно, чтобы функция распределения системы была равна произведению функций распределения составляющих:

.

Кроме того, для непрерывных величин это условие равносильно следующему

.

(Доказательство см. в [1].)

Для независимых случайных величин , т.е. функция регрессии , , т.е. функция регрессии , а значит, линии регрессии −прямые, параллельные координатным осям.

Пример. Задана плотность вероятности совместного распределения системы

Найдем

.

.

Мы видим, что , т.е. случайные величины и являются независимыми.