Лабор. ТП 3

Лабораторная работа

нагрев массивных тел при граничных условиях третьего рода

1. Цель работы

1.1. Оценить изменение температуры в центре и на поверхности образца в процессе нагрева опытным путем.

1.2. Определить графоаналитическим методом температуру в центре и на поверхности образца в конце заданного периода нагрева.

1.3. Сравнить расчетные значения температуры с опытными в конце процесса нагрева изделия.

2. теоретическая часть

При нагревании или охлаждении тела температура в каждой точке его непрерывно меняется во времени. Тепловое состояние тела, при котором температура является функцией координат и времени, называется нестационарным (неустановившимся)

t = f (x, y, z, )

В таком режиме работает кладка печей периодического действия (печи с выдвижным подом, нагревательные колодцы, мартеновские печи), а также насадка регенераторов.

Процесс нестационарной теплопроводности внутри твердого тела в одномерном случае ( плоская бесконечная стенка) описывается дифференциальным уравнением теплопроводности

, (1)

где ­­ – коэффициент температуропроводности, м²/с.

, (2)

где  - коэффициент теплопроводности, Вт/м*град;

С_р – удельная массовая теплоемкость, Дж/кг*град;

 - плотность, кг/м³.

Коэффициент температуропроводности характеризует скорость изменения температуры внутри тела и показывает отношение способности тела проводить теплоту теплопроводностью к способности ее аккумулировать.

Для получения конкретного решения уравнения (1) необходимо задать условия однозначности. Условия однозначности включают:

1. Геометрические условия, характеризующие форму и размеры тела;

2. Физические условия, включающие такие свойства тела и среды, как теплопроводность , теплоемкость С_р, плотность , температуропроводность и др.;

3. Начальные условия, которые характеризуют распределение температуры в теле в начале процесса;

4. Граничные условия, которые дают сведения об условиях теплообмена на поверхности тела( на границе между окружающей средой и поверхностью).

Граничные условия могут быть заданы несколькими способами.

Граничные условия первого рода характеризуются заданием температуры тела для каждого момента времени

t_пов = f (x, y, z, ),

в частном случае

t_пов = const.

Граничные условия второго рода характеризуются заданием теплового потока, поступающего на поверхность тела, для каждого момента времени

q_пов = f (x, y, z, ),

в частном случае

q_пов = const.

При граничных условиях третьего рода задается температура окружающей среды t_Ж и закон теплообмена между поверхностью тела и окружающей средой. При передаче теплоты на поверхность тела конвекцией плотность теплового потока определяется законом Ньютона – Рихмана:

q_к = _к ( t_ж – t_пов ), (3)

где _к – коэффициент теплоотдачи конвекцией, Вт/м²*град;

t_ж, t_пов – температура окружающей среды (жидкости или газа) и поверхности тела (стенки), град.

Если тепловой поток на поверхность тела передается излучением, он определяется по закону Стефана – Больцмана

, (4)

где – приведенная степень черноты тепловоспринимающей поверхности и кладки печи;

C₀ – 5,67 Вт/м²К⁴ – коэффициент излучения абсолютно черного тела;

T_ж, T_пов – абсолютная температура окружающей среды и поверхности тела, К.

Внутрь тела теплота передается теплопроводностью по закону Фурье:

q_т = -. (5)

Граничное условие третьего рода можно представить в виде уравнения теплового баланса на поверхности

(6)

или по аналогии с законом конвекции

_изл( t_ж – t_пов ) = - , (7)

где _изл – коэффициент теплоотдачи излучением (условный) , Вт/м² гр.

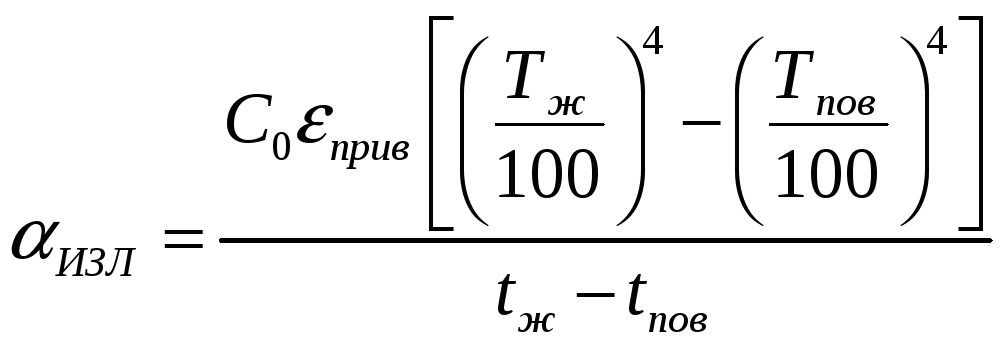(8)

При граничных условиях четвертого рода два тела находятся в плотном контакте между собой. Передача теплоты осуществляется теплопроводностью. В этом случае должно выполняться равенство температур на границе и тепловых потоков по обе стороны от границы раздела

. (9)

В данной работе процесс нагревания тела осуществляется при граничных условиях третьего рода.

Дифференциальное уравнение (1) с заданными условиями однозначности дает полное математическое описание задачи нестационарной теплопроводности.

Из величин, входящих в уравнение (1), можно составить комплекс

, (10)

который называется числом Фурье и характеризует безразмерное время нагревания (или охлаждения) тела (значение «» заменено толщиной прогрева ).

Из граничного условия (7) можно составить комплекс

(11)

который называется числом Био и представляет собой отношение внутреннего теплового сопротивления к внешнему тепловому сопротивлению .

В этих выражениях:

 - время нагревания, с;

 - определяющий размер (прогреваемая толщина), м.

Решение задачи может быть представлено в виде зависимости, связывающей между собой безразмерные величины, характерные для рассматриваемого процесса

, (12)

где - безразмерная (относительная избыточная) температура в некоторой точке тела;

- безразмерная координата;

t₀ – начальная температура тела.

Для определения температуры составлены номограммы, связывающие  с Bi и Fo при X=0 ( середина пластины) и X=1 (поверхность пластины), которые приведены на рис. 1 и 2.

Рис.1. Зависимость безразмерной температуры от чисел Bi и Fo для нагревания поверхности пластины при граничном условии третьего рода

Рис.2. Зависимость безразмерной температуры от чисел Bi и Fo для нагревания центра пластины при граничном условии третьего рода

Все тела в зависимости от характера распределения температуры внутри них делятся на термически тонкие и термически массивные.

К тонким относят тела с малым внутренним тепловым сопротивлением (в пределе  0), к массивным относятся тела с относительно большим тепловым сопротивлением (в пределе  ). У тонкого тела тепловое сопротивление переносу теплоты теплопроводностью ( внутреннее ) от его поверхности к середине значительно меньше теплового сопротивления теплоотдачи (внешнего ), т.е.

<<

Число Био является критерием термической массивности тел. Для термически тонких тел Bi0, в тонких телах перепад температур по сечению практически отсутствует. Для массивных тел Bi, при нагревании и охлаждении их наблюдается значительный перепад температур по сечению и требуется производить выдержку для выравнивания температуры.

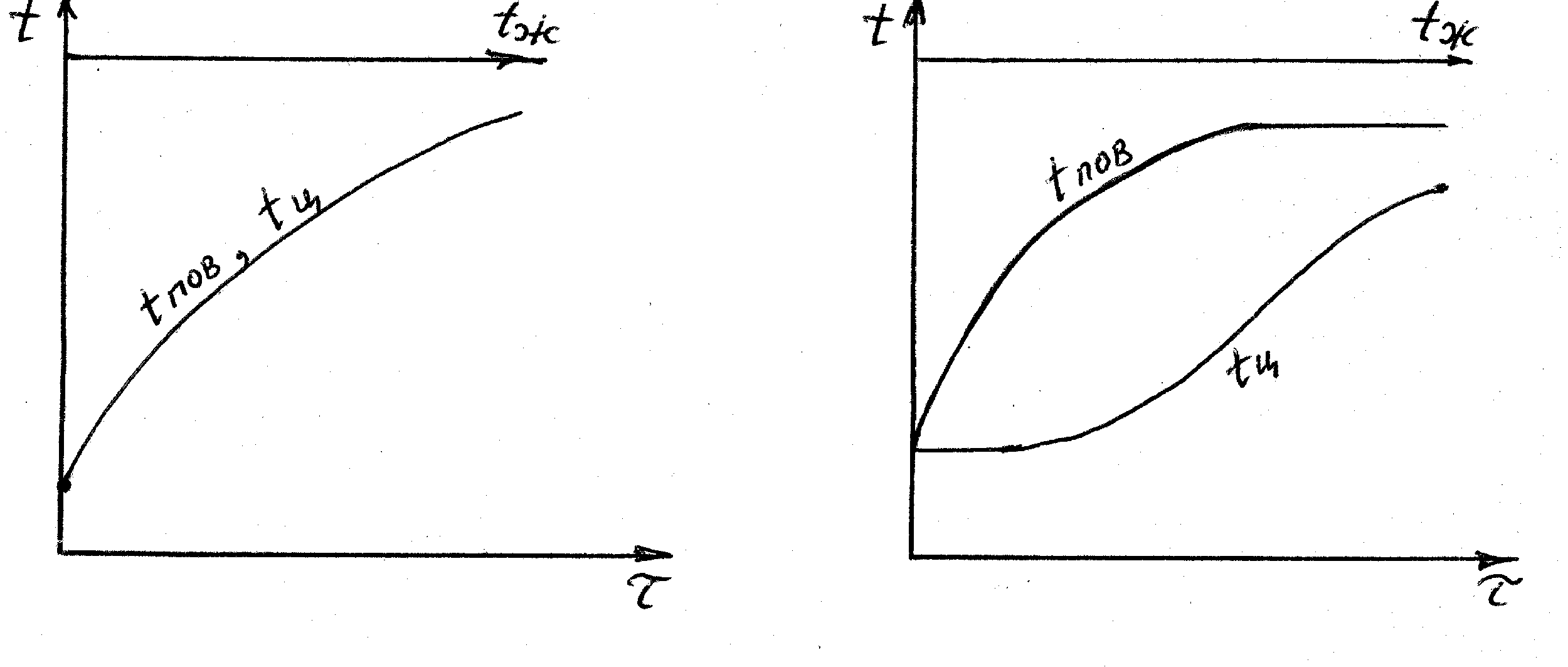
Изменение температуры во времени на поверхности t_пов и в середине t_ц неограниченной пластины при граничных условиях третьего рода (t_ж=const ) для идеально тонких и идеально массивных тел при двухстороннем нагреве представлено на рис. 3, а и б.

а ) б)

Рис.3. Изменение температуры поверхности и середины пластины тонких (а) и массивных (б) тел

На рис. 4 показано распределение температуры по толщине бесконечной пластины в различные периоды времени нагрева.

а) б)

Рис.4. Распределение температуры по толщине пластины

а) при Bi  0

б) при Bi  ∞

Из опыта работы нагревательных устройств установлено, что к тонким телам можно отнести такие, у которых Bi< 0,25, а при Bi  0,5 тела следует считать массивными.

3. Описание установки

Установка состоит из муфельной печи А, температура которой измеряется термопарой 1 в комплекте с регистрирующим прибором В (рис. 5).

В печь помещается шамотный кирпич С с двумя термопарами: термопара 2 измеряет температуру середины кирпича, термопара 3 – температуру поверхности. Выводы термопар подключены к тому же прибору В. Номера термопар соответствуют точкам переключателя D.

4. Порядок выполнения работы

4.1. Включить электрическую печь и нагреть ее до температуры 500-600 °С (включение осуществляется только лаборантом или препо­давателем) .

4.2 . Подготовить журнал наблюдений (табл.1 ).

4.3. Поместить кирпич в центр печи, вывести термопары 2 и 3 через отверстие дверцы, подключить термопары к регистрирующему прибору.

Рис.5 Схема установки

А - печь; В – милливольтметр; С – кирпич; D – переключатель;

1, 2, 3, - точки замера температуры.

4.4. Снимать показания милливольтметра для каждой из трех то­чек: первые две минуты через 30 с., затем через 1 мин. Общее время нагрева задается преподавателем (12-14 мин.).

4.5. Полученные данные занести в журнал наблюдений.

4.6. С помощью градуировочной таблицы перевести милливольты в градусы Цельсия. Так как холодные спаи термопар находятся при комнатной температуре, для получения истинных значений температу­ры в точках 1, 2, 3 следует сделать перерасчет

t_ист = t_изм + t_ос (13)

где t _ист - истинное значение температуры, ⁰С;

t _изм - значение температуры по градуировочной таблице, ⁰С;

t _ос - температура окружающего воздуха, ⁰С (по термомет­ру в лаборатории).

5. РАСЧЕТНАЯ ЧАСТЬ

5.1. На одном графике в координатах t -  построить три экспериментальные кривые:

t_ж = t печи =;

t_ц = ;

t_пов = ,

где t_ц - температура середины (центра) кирпича, ⁰C;

t_пов -температура поверхности кирпича, ⁰С.

5.2. Вычислить среднеарифметическое значение температуры пе­чи за период нагрева _печи и в расчетах использовать ее как _печи = const.

Таблица 1

Журнал наблюдений

Время опыта мин.	Показания прибора, mV			Температура tист, град
	печь	середина кирпича	поверхность кирпича	печь	середина кирпича	поверхностькирпича	воздух
0,5 1 1,5 2 3 4 - - - - 12

5.3. Вычислить коэффициент теплоотдачи излучением _изл по формуле (8)

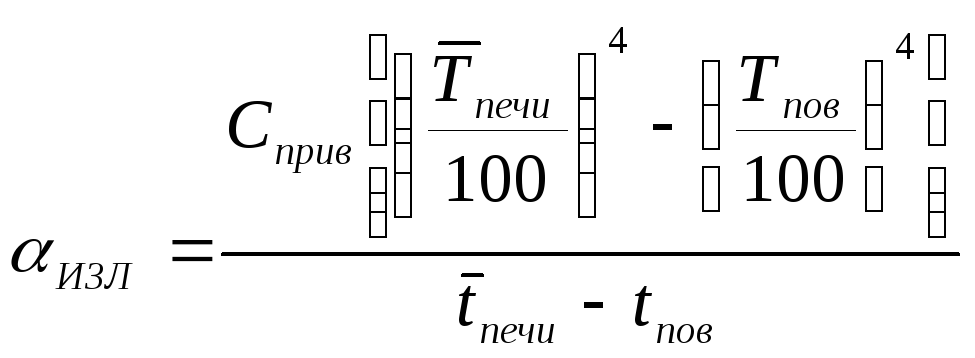
где t_пов, T_пов – температура поверхности кирпича на конец опыта, соответственно, ^оС и К,

С_прив - приведенный коэффициент излучения, Вт/(м² *К⁴),

С_прив =,

С_о - коэффициент излучения абсолютно черного тела;

С_о = 5,67 Вт/(м² *К⁴),

- приведенная степень черноты. Для системы муфель-кирпич рассчитывается по формуле

, (14)

где - степень черноты поверхности кирпича и муфеля;

- угловой коэффициент излучения (отношение поверхности теплообмена кирпича и муфеля), для данной системы φ = 0,27.

5.4. Вычислить число Био (Bi) по формуле (11)

,

где  - условная толщина прогреваемого слоя: она составляет 0,032 м ( половина толщины кирпича).

λ – коэффициент теплопроводности кирпича при средней темпе­ратуре его по массе в конце периода нагрева, Вт/м*град.

Средняя по массе температура вычисляется по формуле

= t_пов - 2/3( t_пов - t_ц) . (15)

Коэффициент теплопроводности для шамотного кирпича рассчитывается по формуле :

λ= 0,84 + 0.6*10^-3 Вт/м*град, (16)

5.5. Вычислить число подобия Фурье (Fo) по формуле (10)

,

где  - время нагревания, с;

- коэффициент температуропроводности, м² /с;

С_р - удельная массовая теплоемкость, Дж/кг*град;

 - плотность, кг/м³.

Для шамотного кирпича

С_р = ( 0,88 + 0.00023)*10³ . Дж/кг*град , (17)

=1800 кг/м³.

5.6. По рассчитанным значениям Fo и Bi, используя номограммы на рис. 1 и 2, определить безразмерные температуры поверхности и середины кирпича .

5.7. Рассчитать температуры поверхности t_пов и середины t_ц кирпича в конце периода нагрева, используя значения и , найденные с помощью номограмм;

t_пов = _печи - ( _печи – t₀ )

t_ц = _печи - ( _печи – t₀ ),

где t₀ - начальная температура кирпича (при  = 0), равная тем­пературе воздуха в лаборатории.

5.8. Сравнить расчетные значения температур с полученными в опыте. Занести результаты в табл. 2.

Таблица 2

Сравнительные результаты работы

Общее время нагрева, мин.	Температура в конце периода нагрева, 0С
	поверхности tпов		середины tц
	опытная	расчетная	опытная	расчетная