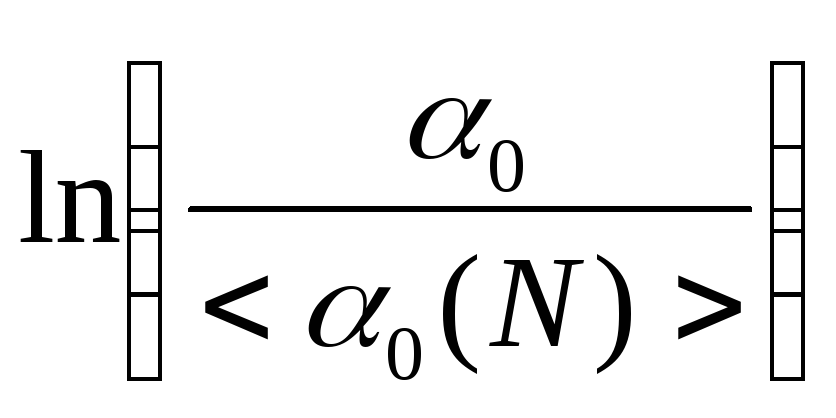Лабораторная работа 5
.docФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО
МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г. И. НОСОВА
Филиал МГТУ в г. Белорецке
Изучение затухающих колебаний физического маятника
Методические указания к лабораторной работе №5 по дисциплине
«Общая физика.
Механика. Молекулярная физика и термодинамика»
для студентов специальностей 150106, 150105, 150201, 150404, 2005030.
Магнитогорск
2012
Составитель: Мигранова С.Г.
Методические указания к лабораторной работе №5 по дисциплине «Общая физика. Механика. Молекулярная физика и термодинамика» для студентов специальностей 150106, 150105, 150201, 150404, 2005030. Магнитогорск: МГТУ, 2012.
Рецензент: Дубосарская Ю.М.
Лабораторная работа № 5
Изучение затухающих колебаний физического маятника
Цель работы: изучение затухающих колебаний, определение основных характеристик затухающих колебаний.
Приборы и принадлежности: физический маятник, постоянный магнит, секундомер, весы.
Краткая теория
Затухающие колебания. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленной потерей энергии колебательной системой. Затухание колебаний в механических системах вызывается в основном трением, сопротивлением среды и возбуждением в ней волн.
Н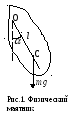 айдем
дифференциальное уравнение, описывающее
свободные затухающие колебания
физического маятника. Если колеблющееся
тело нельзя представить как материальную
точку, маятник называют физическим.
Движение маятника описывается уравнением
динамики вращательного движения
айдем
дифференциальное уравнение, описывающее
свободные затухающие колебания
физического маятника. Если колеблющееся
тело нельзя представить как материальную
точку, маятник называют физическим.
Движение маятника описывается уравнением
динамики вращательного движения
![]() ,
где
,
где
![]() -
результирующий момент сил, действующих
на систему,
-
результирующий момент сил, действующих
на систему,
![]() -
момент инерции системы,
-
момент инерции системы,
![]() -
угловое ускорение:
-
угловое ускорение:
![]() .
На физический маятник действует момент
силы тяжести
.
На физический маятник действует момент
силы тяжести
![]() и момент сил сопротивления, при малых
отклонениях пропорциональный угловой
скорости
и момент сил сопротивления, при малых
отклонениях пропорциональный угловой
скорости
![]() .
.
![]()
![]()
При малых колебаниях
![]() ,
тогда
,
тогда
![]() (1) - дифференциальное
уравнение затухающих колебаний
физического маятника.
(1) - дифференциальное
уравнение затухающих колебаний
физического маятника.
Введем обозначения физических характеристик:
![]() -
циклическая частота свободных незатухающих
колебаний маятника,
-
циклическая частота свободных незатухающих
колебаний маятника,
![]() - циклическая
частота затухающих колебаний,
- циклическая
частота затухающих колебаний,
![]() -
период затухающих колебаний.
-
период затухающих колебаний.
![]() (2) -
уравнение
затухающих колебаний, полученное при
выполнении условий: отклонения маятника
малы, момент сил сопротивления
пропорционален скорости, выполняется
неравенство
(2) -
уравнение
затухающих колебаний, полученное при
выполнении условий: отклонения маятника
малы, момент сил сопротивления
пропорционален скорости, выполняется
неравенство
![]() .
.
Решение дифференциального уравнения затухающих колебаний имеет следующий вид:
![]() ,
(3)
,
(3)
г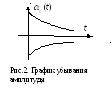 де
де
![]() (4) - амплитуда затухающих колебаний,
(4) - амплитуда затухающих колебаний,
![]() (5) - коэффициент затухания.
(5) - коэффициент затухания.
График зависимости
![]() при начальной фазе
при начальной фазе
![]() имеет вид экспоненты, причем, чем меньше
коэффициент β, тем амплитуда убывает
слабее.
имеет вид экспоненты, причем, чем меньше
коэффициент β, тем амплитуда убывает
слабее.
Затухающие колебания
- непериодические, т.к.
![]() в начальный момент никогда не повторяется.
Однако
в начальный момент никогда не повторяется.
Однако
![]() обращается в ноль и достигает max
и min
через один и тот же промежуток времени
обращается в ноль и достигает max
и min
через один и тот же промежуток времени
![]() .
.
Промежуток времени
![]() ,
в течение которого амплитуда затухающих
колебаний уменьшается в е раз, называется
временем релаксации.
,
в течение которого амплитуда затухающих
колебаний уменьшается в е раз, называется
временем релаксации.
![]()
![]()
![]() (6)
(6)
Логарифмическим
декрементом затухания называется
безразмерная величина
![]() ,
равная логарифму отношения амплитуды
в момент времени
,
равная логарифму отношения амплитуды
в момент времени
![]() к амплитуде через период:
к амплитуде через период:
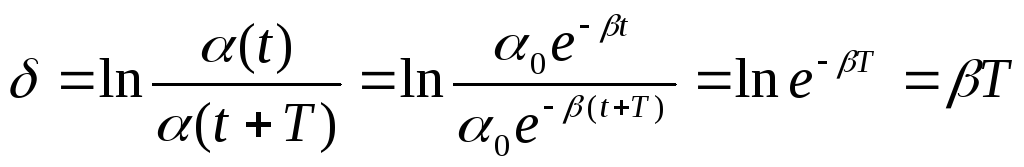
![]() ,
(7), где
,
(7), где
![]() - число колебаний, в течение которых
амплитуда уменьшается в е раз.
- число колебаний, в течение которых
амплитуда уменьшается в е раз.
Добротностью
колебательной системы называется
безразмерная величина
![]() ,
равная
,
равная
![]() ,
умноженным на отношение энергии в момент
времени
,
умноженным на отношение энергии в момент
времени
![]() к разности энергий через период:
к разности энергий через период:
![]()
Т.к. полная энергия
пропорциональна квадрату амплитуды,
т.е.
![]() ,
то
,
то
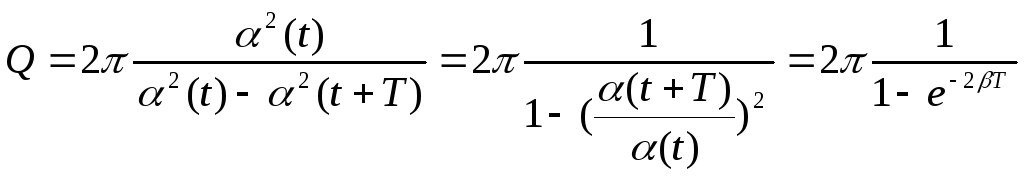
При малых значениях
логарифмического декремента затухания
(![]() <<1)
<<1)
![]() и добротность
и добротность
![]() (8)
(8)
Теория метода и описание установки
Установка для изучения затухающих колебаний представляет собой физический маятник, который совершает колебания относительно точки подвеса О. Нижней частью маятника является полукруглая алюминиевая пластина. При движении маятника в магнитном поле постоянного магнита в нем индуцируются вихревые токи (токи Фуко), обусловливающие заметное магнитное взаимодействие поля и пластины. Сила этого взаимодействия всегда направлена против перемещения (правило Ленца) и пропорциональна скорости движения пластины. Изменяя расположение магнита относительно пластины, можно изменять силу сопротивления при колебаниях физического маятника.
Е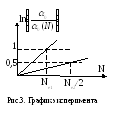 сли
экспериментально найти
сли
экспериментально найти
![]() и
и
![]() ,
то по формулам (6), (7) и (8) можно вычислить
коэффициент затухания
,
то по формулам (6), (7) и (8) можно вычислить
коэффициент затухания
![]() ,
логарифмический декремент затухания
,
логарифмический декремент затухания
![]() ,
время релаксации
,
время релаксации
![]() и декремент затухания
и декремент затухания
![]() .
Зная момент инерции маятника, можно
найти коэффициент сопротивления r
по формуле (5). Зависимость амплитуды
.
Зная момент инерции маятника, можно
найти коэффициент сопротивления r
по формуле (5). Зависимость амплитуды
![]() - экспоненциальная (формула (4)) и поэтому
лучше строить графики этих зависимостей
в логарифмическом масштабе. Если учесть,
что
- экспоненциальная (формула (4)) и поэтому
лучше строить графики этих зависимостей
в логарифмическом масштабе. Если учесть,
что
![]() ,
то
,
то
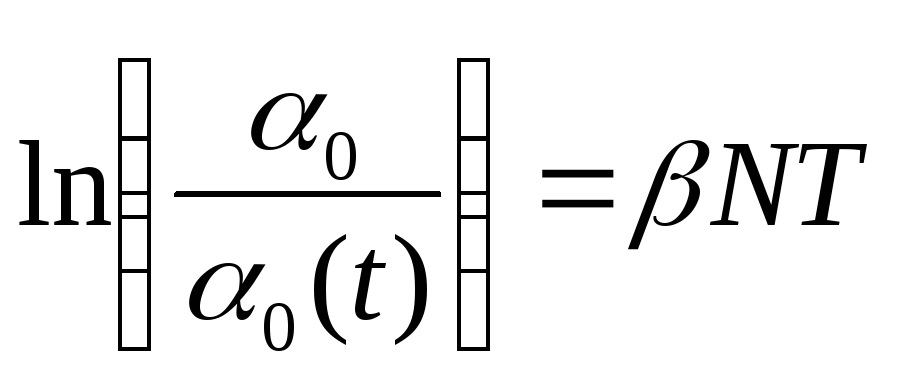 ,
где
,
где
![]() – число
– число
колебаний. График
зависимости
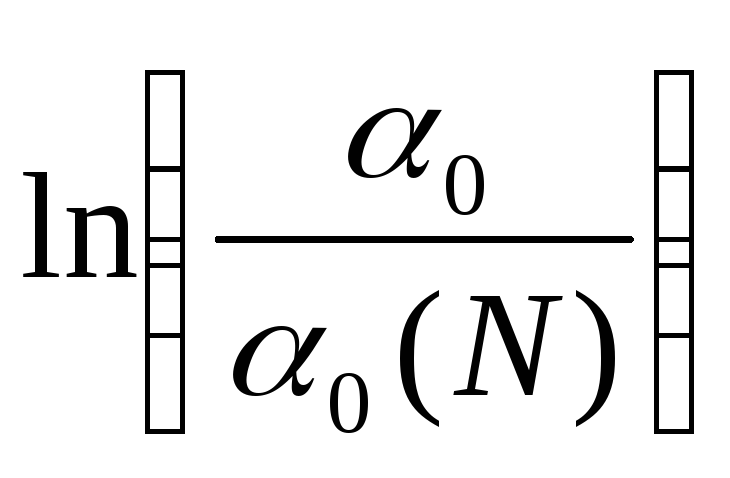 от
от
![]() будет иметь вид прямой, проходящей через
начало координат. На графике легко
определяются
будет иметь вид прямой, проходящей через
начало координат. На графике легко
определяются
![]() по точке пересечения с горизонтальной
прямой, соответствующей значению
по точке пересечения с горизонтальной
прямой, соответствующей значению
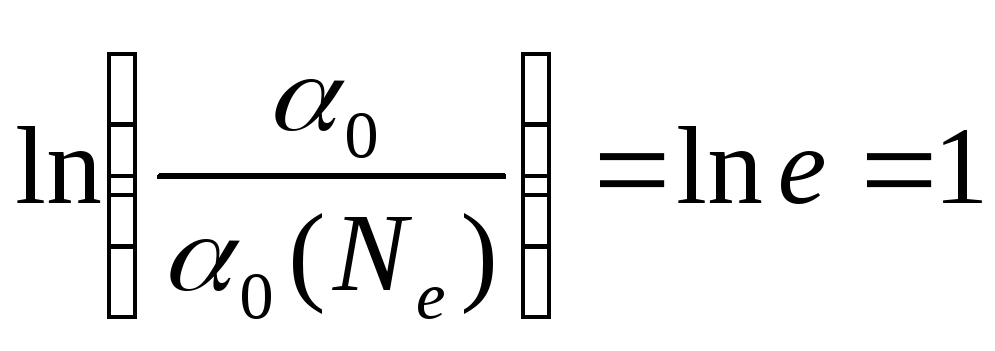 .
Если график не пресекается с ординатой,
равной единице, то можно заменить 1 на
0,5, но тогда полученное значение
.
Если график не пресекается с ординатой,
равной единице, то можно заменить 1 на
0,5, но тогда полученное значение
![]() нужно умножить на 2.
нужно умножить на 2.
Измерения и обработка результатов измерений
-
Отклонить маятник на определенное количество делений
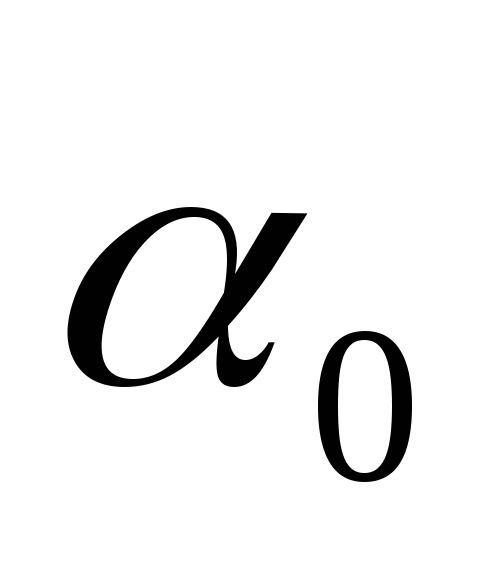 ,
отпустить его и сделать ряд отсчетов
амплитуды одинакового знака через
одинаковое число колебаний (не
останавливая маятник). Эти измерения
повторить еще два раза и занести данные
в таблицу.
,
отпустить его и сделать ряд отсчетов
амплитуды одинакового знака через
одинаковое число колебаний (не
останавливая маятник). Эти измерения
повторить еще два раза и занести данные
в таблицу.
-
Определить средние значения амплитуд через
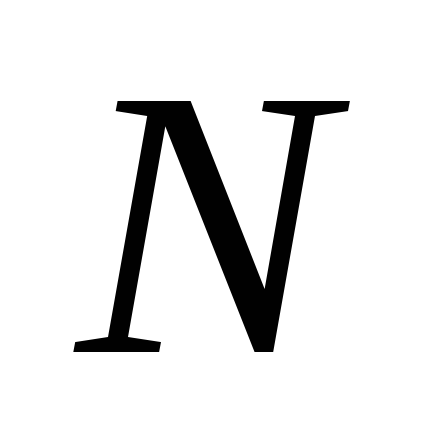 колебаний по формуле
колебаний по формуле
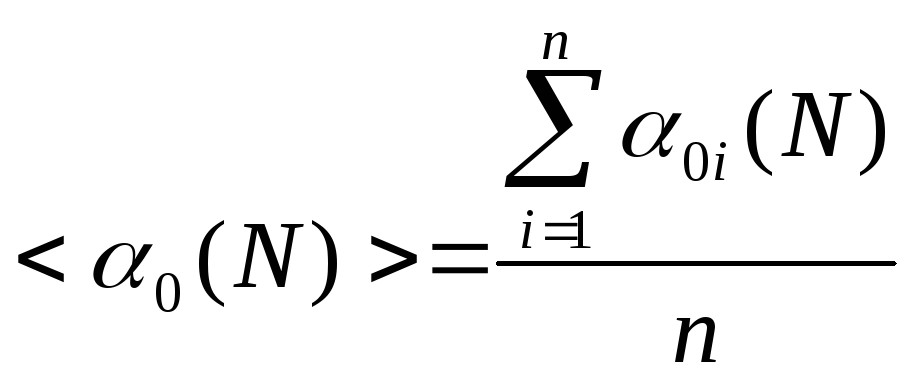 .
. -
Найти отношения
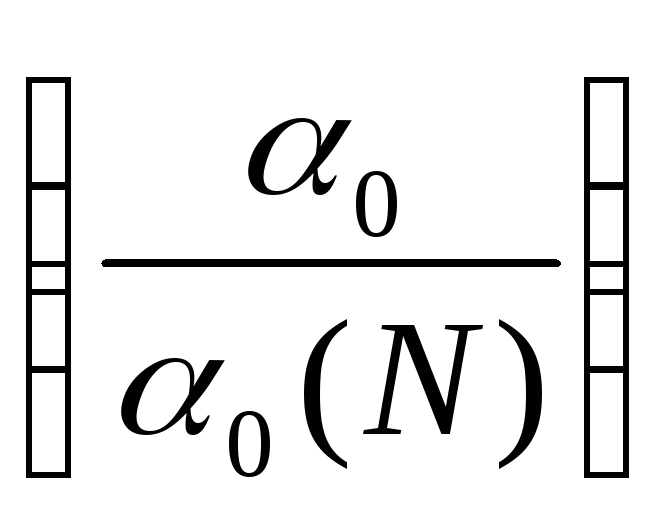 и
и
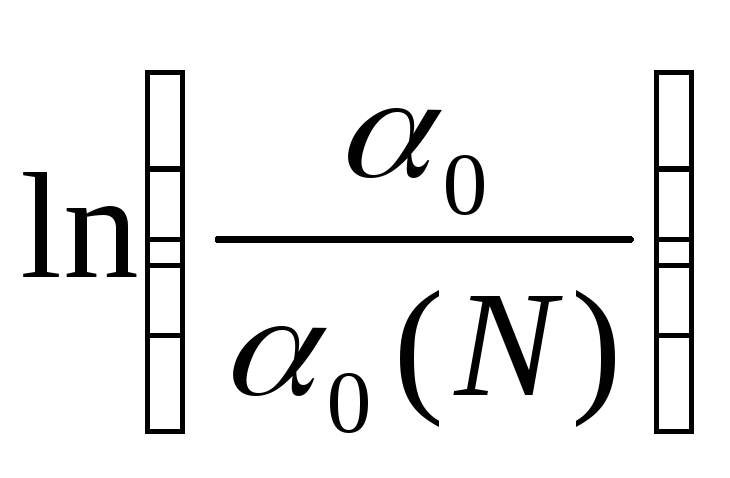 и построить график зависимости
и построить график зависимости
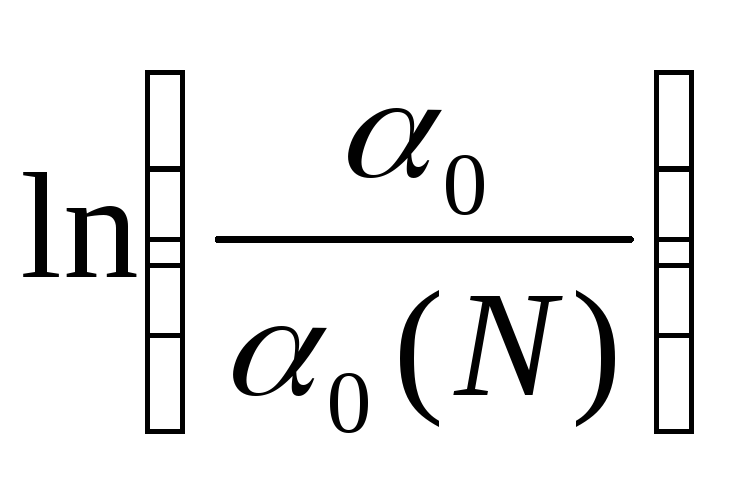 от
от
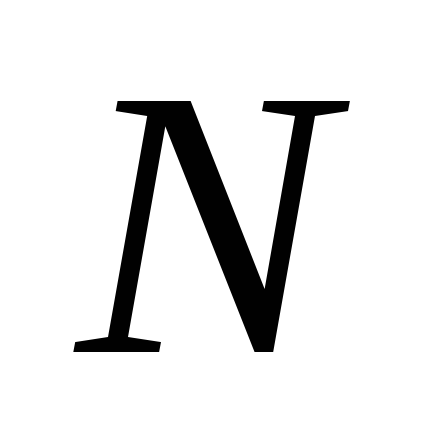 .
. -
Провести аналогичные измерения и расчеты при двух различных положениях постоянного магнита, внести результаты в табл.1 и построить графики.
Табл.1
|
Усло-вия опыта |
Число коле-баний, N |
Амплитуда,
|
Среднее Значение
|
|
||
|
1-е изм. |
2-е изм. |
3-е изм. |
||||
|
Без маг-нита |
0 5 10 15 20 |
|
|
|
|
|
|
С маг-нитом 1 |
0 5 10 15 20 |
|
|
|
|
|
|
С маг-нитом 2 |
0 5 10 15 20 |
|
|
|
|
|
-
По графикам определить число колебаний, за которое амплитуда убывает в
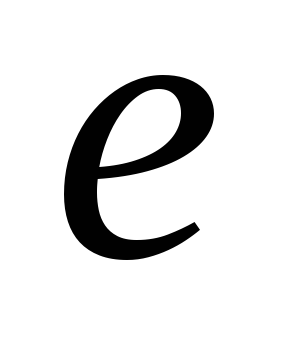 раз.
раз. -
Определить период колебаний маятника для всех трех случаев.
-
По формулам (6), (7) и (8) вычислить коэффициент затухания
 ,
логарифмический декремент затухания
,
логарифмический декремент затухания
 ,
время релаксации
,
время релаксации
 и декремент затухания
и декремент затухания
 и коэффициент сопротивления
и коэффициент сопротивления
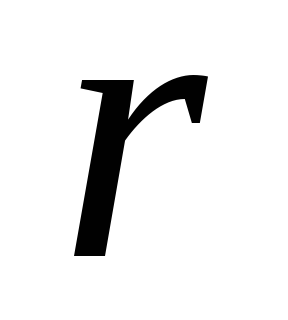 .
Занести результаты в табл.2.
.
Занести результаты в табл.2.
Табл.2
|
Условия опыта |
N
|
T |
β |
τ |
δ |
r |
|
Без магнита |
|
|
|
|
|
|
|
С магнитом 1 |
|
|
|
|
|
|
|
С магнитом 2 |
|
|
|
|
|
|
Контрольные вопросы
-
Как записать второй закон Ньютона для затухающих колебаний в данной лабораторной работе и как получить из него дифференциальное уравнение колебаний?
-
Каков физический смысл величин
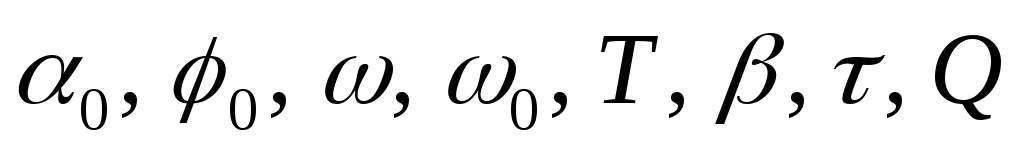 ,
рассматриваемых и определяемых в данной
работе? Какова связь между ними? Как
они изменяются с увеличением коэффициента
сопротивления
,
рассматриваемых и определяемых в данной
работе? Какова связь между ними? Как
они изменяются с увеличением коэффициента
сопротивления
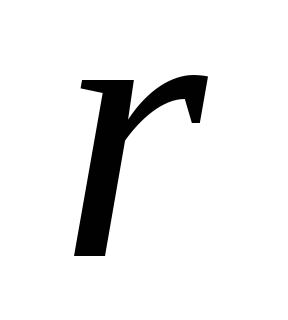 ?
? -
Как записать решение уравнения затухающих колебаний? Как выглядит график зависимости
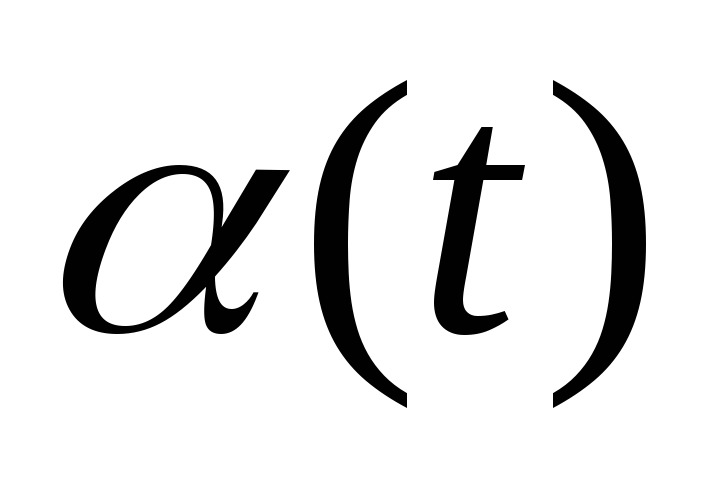 для
затухающих колебаний?
для
затухающих колебаний? -
Как осуществляется определение основных характеристик затухающих колебаний в данной работе?
Литература
-
Савельев И.В. Курс общей физики, т.1 Механика. Молекулярная физика: Учебное пособие. –М.: Наука,1982. – 432 с.
-
Сивухин Д.В. Общий курс физики. Учеб. Пособие: Для вузов. В 5 т. Т. I. Механика. – М.: ФИЗМАТЛИТ, 2002. – 560 с.
-
Трофимова Т.И. Курс физики: Учеб. Пособие для вузов. – М.: Высш. шк., 2001. – 542 с.
-
Рогачев Н.М. Курс физики: Учебное пособие. – СПб.:Издательство «Лань», 2008. – 448 с.