
- •Министерство образования и науки Российской Федерации
- •Глава 1. Общие сведения по геодезии
- •1.2. Роль геодезии в народном хозяйстве и обороне страны
- •1.3. Связь геодезии с другими научными дисциплинами
- •Глава 2. Сведения о фигуре земли и системах координат, применяемых в геодезии
- •2.2. Основная уровенная поверхность. Геоид. Эллипсоид.
- •2.3. Расчёт размеров участка сферической (уровенной) поверхности Земли для обобщения её до горизонтальной плоскости
- •2.4. Определение положения точек земной поверхности и применяемые для этого в геодезии системы координат
- •2.4.1. Метод проекций в геодезии. Величины, подлежащие измерению
- •2.4.2. Понятия о плане, карте, профиле линии местности
- •2.4.3. Астрономические и геодезические координаты.
- •2.4.4. Влияние кривизны Земли на определение высот точек
- •2.4.5. Проекция Гаусса – Крюгера*. Зональная и условная
- •2.4.6. Зональная система плоских прямоугольных координат
- •2.4.7. Условная система прямоугольных координат на плоскости
- •Глава 3. Ориентирование линий
- •3.5. Прямая и обратная геодезические задачи на плоскости
- •Глава 4. Элементы теории погрешностей геодезических измерений
- •4.1. Общие сведения об измерениях
- •4.2. Погрешности результатов измерений
- •4.3. Задачи теории погрешностей измерений
- •4.4. Равноточные измерения
- •4.4.1. Вычисление наиболее точного по вероятности значения
- •4.4.2. Оценка точности результатов ряда равноточных измерений.
- •4.4.3. Оценка точности функций измеренных величин
- •4.4.4. Оценка точности результатов ряда двойных равноточных измерений
- •4.4.5. Примеры оценки точности результатов равноточных измерений одной величины и функций независимо измеренных величин
- •4.5. Неравноточные измерения
- •4.5.1. Общая арифметическая середина. Веса результатов измерений
- •4.5.2. Средняя квадратическая погрешность единицы веса
- •4.5.3. Средняя квадратическая погрешность и вес общей арифметической середины
- •4.5.4. Вычисление весов функций независимых аргументов
- •4.5.5. Порядок математической обработки результатов неравноточных измерений
- •Глава 5. Измерения в геодезии
- •5.1.1. Принцип измерения горизонтального угла
- •Основные оси теодолита:
- •Основные плоскости теодолита:
- •5.1.2. Эксцентриситет алидады, исключение его влияния на отсчёт по лимбу
- •5.1.3 Уровни геодезических приборов
- •5.1.4. Зрительные трубы геодезических приборов
- •Основные характеристики зрительных труб
- •Параллакс сетки нитей, его устранение
- •5.1.5. Отсчетные устройства
- •5.1.6 Вертикальный круг.
- •Теория вертикального круга
- •5.1.7. Поверки и юстировка теодолита
- •5.1.8. Измерение горизонтальных углов
- •Измерение одиночного горизонтального угла способом приёмов
- •Собственно измерение горизонтального угла
- •Программа наблюдения направлений
- •Журнал измерения горизонтальных углов
- •Проложение теодолитных ходов
- •Глава 6. Нивелирование
- •6.1. Геометрическое нивелирование
- •Способ геометрического нивелирования - "из середины"
- •Способ геометрического нивелирования - "вперёд"
- •6.2. Поверки и юстировка нивелира с уровнем при трубе
- •6.3. Определение разности пяток нивелирных реек.
- •Глава 7. Линейные измерения
- •7.1. Измерение расстояний нитяным дальномером
- •7.2.1. Компарирование землемерной ленты (рулетки)
- •7.2.2. Обозначение отрезков линий на местности
- •7.2.3. Собственно измерение длин линий.
- •Глава 8. Геодезические работы при изыскании и строительстве автомобильных дорог
- •8.1. Понятие о трассе
- •8.2. Круговые и переходные кривые на трассе
- •8.3. Трассирование
- •8.4. Детальная разбивка кривых
- •8.5. Составление профилей
- •Литература
- •Оглавление
6.3. Определение разности пяток нивелирных реек.
Разностью пяток (разностью высот нулей) нивелирной рейки называется смещение начала счёта делений красной стороны рейки относительно ноля (совмещён с низом оковки рейки) делений чёрной стороны.
В 10 - 15 м
от нивелира на башмак устанавливают
нивелирную рейку №1. Вращением
элевационного винта совмещают изображения
концов пузырька цилиндрического
контактного уровня, берут отсчёты по
чёрной
![]() и красной
и красной![]() сторонам рейки, которые записывают в
журнал. Вычитая из второго отсчёта
первый, определяют разность пяток рейки.
Подобные действия выполняют для рейки
№ 2. Полученные разности используют при
контроле определения превышений на
станции.
сторонам рейки, которые записывают в
журнал. Вычитая из второго отсчёта
первый, определяют разность пяток рейки.
Подобные действия выполняют для рейки
№ 2. Полученные разности используют при
контроле определения превышений на
станции.
- 103 -
Глава 7. Линейные измерения
Определение длин отрезков линий местности выполняется или непосредственно, или косвенно с помощью различных дальномеров. Точность линейных измерений колеблется от 1:200 до 1:1000 000.
7.1. Измерение расстояний нитяным дальномером
Современные теодолиты снабжены устройствами для опреде-ления длин отрезков линий местности - оптическими или электронными дальномерами. Таким образом, при наличии вертикального круга и дальномера теодолит трансформировался в тахеометр*.
Измерение расстояний D1 оптическими дальномерами основано на решении равнобедренного треугольника (рис. 7.1), вершина которого располагается в одной из точек измеряемого отрезка AB, а основание (базис) PQ в другой.
Оптические дальномеры различают:
1) с постоянным (диастимометрическим**) углом φи перемен- ным базисом l;
2) с переменным (параллактическим) углом и постоянным базисом.

Рис. 7.1. Оптический дальномер
________
* Тахеометрия - скороизмерение.
** Диастимометрический - измеряющий расстояние.
- 104 -
Длина D1 отрезка АВ определится из выражения
![]() .
(7.1)
.
(7.1)
Одним из видов оптических дальномеров с постоянным углом и переменным базисом является нитяной дальномер (рис. 7.2).
Он состоит из дальномерных нитей pq сетки нитей зрительной трубы и отвесно расположенной рейки с делениями, служащей базисом.

Рис. 7.2. Нитяной дальномер
Пусть визирная ось kkзрительной трубы тахеометра расположена горизонтально. Лучи от дальномерных нитей p и q, пройдя через объектив и передний фокус F , пересекут рейку в точках P и Q.
Согласно рис. 7.2 можно написать
![]() ,
(7.2)
,
(7.2)
где δ - расстояние от объектива зрительной трубы до оси ZZ' вращения тахеометра, fоб.-фокусное расстояние объектива.
- 105 -
Обозначим
![]() ,
которое называется постоянным дальномера.
С учётом этого обозначения и формулы
(7.1), уравнение (7.2) примет вид
,
которое называется постоянным дальномера.
С учётом этого обозначения и формулы
(7.1), уравнение (7.2) примет вид
![]() .
(7.3)
.
(7.3)
Введём обозначение
![]() ,
(7.4)
,
(7.4)
где К - постоянно и называется коэффициентом нитяного дальномера. С учётом (7.4) искомое расстояние будет
![]() .
(7.5)
.
(7.5)
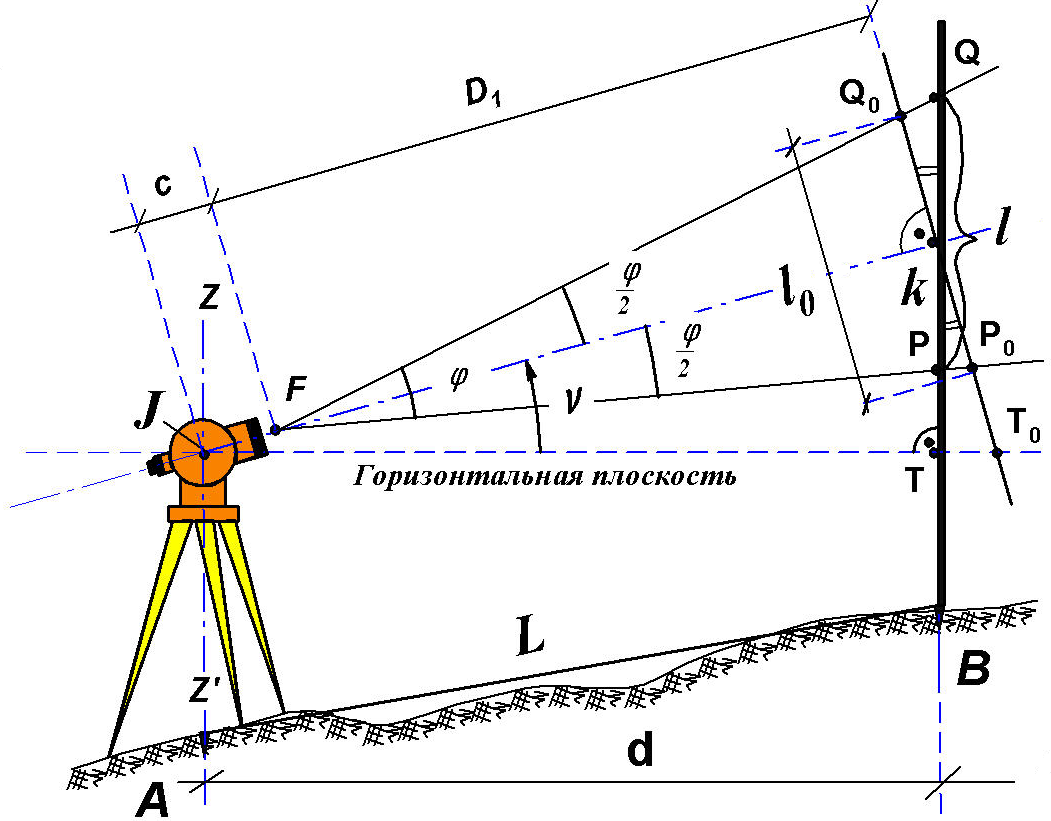
Рис. 7.3. Измерение нитяным дальномером наклонных расстояний
Пусть визирная ось зрительной трубы образует с горизонтальной плоскостью угол v (рис.7.3).
Конечным результатом измерения отрезка линии местности является длина его горизонтального проложения d .
Для случая, когда базис P0Q0 расположен перпендикулярно линии визирования, искомая величина определится из выражения
- 106 -
![]() .
(7.6)
.
(7.6)
В действительности
базис (рейка) располагается в точке
местности по отвесной линии и составляет
с линией визирования угол
![]() .
По этой причине длина
l
базиса не равна
l0.
Выразим длину l0
через длину
l.
Считая углы QQ0k
и PP0k
равными 90º,
.
По этой причине длина
l
базиса не равна
l0.
Выразим длину l0
через длину
l.
Считая углы QQ0k
и PP0k
равными 90º,
найдем
![]() .
(7.7)
.
(7.7)
С учётом (7.7), выражение (7.6) примет вид
![]() .
(7.8)
.
(7.8)
По малости c
и v
можно принять
![]() ,
тогда
,
тогда
![]() .
(7.9)
.
(7.9)
Пусть число делений рейки между проекциями P и Q на неё дальномерных нитей равно n. Цену делений примем равной μ. Тогда длина базиса будет равна
![]() .
(7.10)
.
(7.10)
Если цена делений рейки
в сантиметрах, то
![]() .
Формулу (7.9) для вычисления горизонтального
проложения можно записать в окончательном
виде
.
Формулу (7.9) для вычисления горизонтального
проложения можно записать в окончательном
виде
![]() .
(7.11)
.
(7.11)
Заводы - изготовители
гарантируют значение коэффициента
нитяного дальномера равное
![]() .
Действительное значение коэффициента
определяют на полевом компараторе.
.
Действительное значение коэффициента
определяют на полевом компараторе.
В современных зрительных трубах с внутренним фокусированием постоянное дальномера c очень мало и его во многих случаях можно не учитывать. Формулу (7.11) можно применить в виде
![]() .
(7.12)
.
(7.12)
Точность измерения расстояний нитяным дальномером характеризуется относительной погрешностью
![]() .
.
- 107 -
Пример определения расстояния, измеренного нитяным дальномером: n = 28,3 см, v = + 9º17', K = 100,37.
По формуле (7.12) вычислим
![]() .
.

Рис. 7.4. Определение дальномерного расстояния n:
отсчёт по верхней дальномерной нити (В.Д.Н.) - 100 см;
отсчёт по нижней дальномерной нити (Н.Д.Н.) - 128,3 см;
дальномерное расстояние n = 128,3 - 100 = 28,3 см.
Измерение расстояний стальной мерной лентой
Перед началом полевых работ по измерению длин линий рабочие меры (землемерные ленты и рулетки) следует прокомпарировать.
Компарированием называется процесс сравнения рабочей меры с нормальной, т.е. с мерой, длина которой известна.
Компарирование выполняют на полевых или лабораторных компараторах, а также путём непосредственного сравнения рабочей и нормальной мер.
- 108 -
