Основные оси теодолита:

1) ZZ' - ось вращения алидады горизонтального круга, называемая также вертикальной осью теодолита (рис. 5.3); 2) UU' - ось цилиндрического уровня - касательная к дуге внутрен-ней поверхности продольного сечения ампулы уровня, проведенная в нуль-пункте (рис. 5.3 и 5.5);

3) VV' - визирная ось - прямая, проходящая через перекрестие нитей сетки нитей и оптический центр объектива зрительной трубы;

4) НН' - ось вращения зрительной трубы, называемая также горизон-тальной осью теодолита;

5) О₁О₂ - оптическая ось зрительной трубы - прямая, соединяющая оптические центры объектива и окуляра зрительной трубы.

Основные плоскости теодолита:

1) плоскость лимба - образована внутренними концами штрихов лимба; при измерении углов должна быть неподвижна и горизонтальна;

2) коллимационная плоскость - образована вращением визирной оси зрительной трубы VV' вокруг горизонтальной НН' оси; во время измерений должна быть отвесна и перпендикулярна плоскости лимба.

5.1.2. Эксцентриситет алидады, исключение его влияния на отсчёт по лимбу

Одним из геометрических условий, которое должно выполняться в теодолите, является совмещение оси вращения алидады с центром

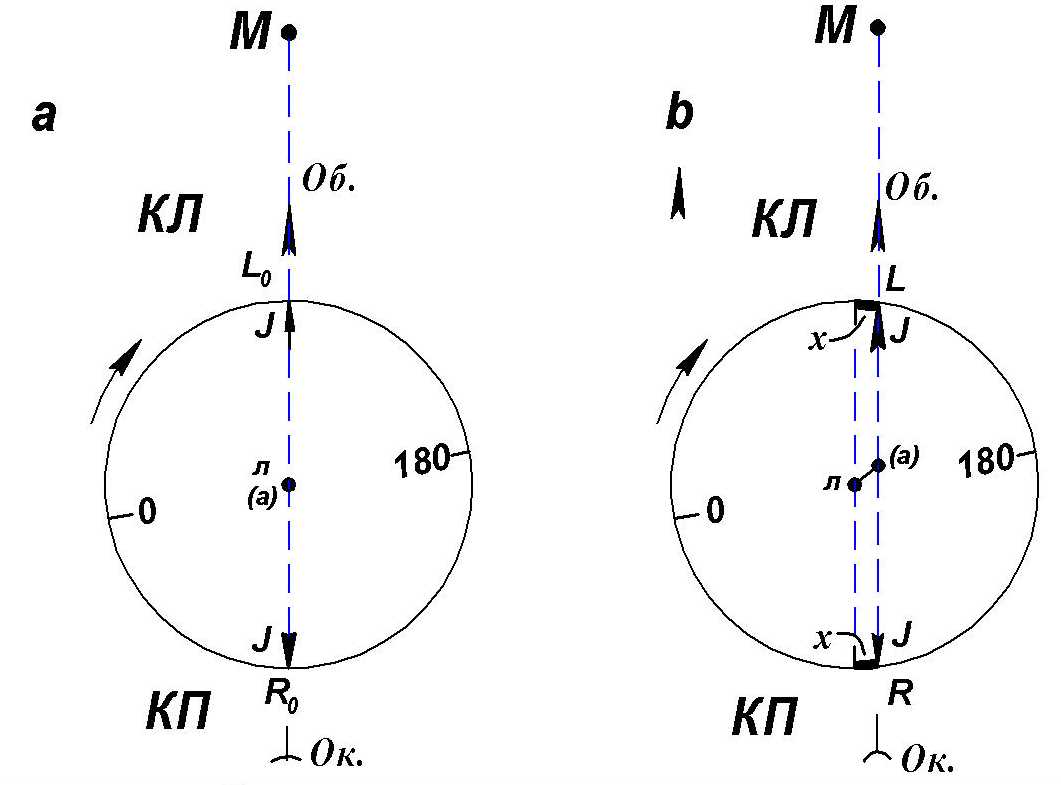
Рис. 5.4. Эксцентриситет алидады горизонтального круга

J - положение отсчётного индекса алидады при двух положениях вертикального круга: КП и КЛ

- 69 -

кольца делений лимба. Не выполнение условия приводит к погрешности в отсчётах по лимбу, называемой эксцентриситетом алидады (см. рис. 5.4). Пусть ось вращения (рис. 5.4-а) алидады (а) совпадает с центром кольца делений лимба л. L₀ и R₀ - диаметрально противоположные отсчёты по лимбу, т.е. . Если ось вращения алидады не совпадает с центром кольца делений лимба, то имеет место наличияэксцентриситета. В этом случае по лимбу будут взяты отсчёты L и R (рис. 5.4-b), ошибочные на величину эксцентриситета x, т.е.

и .

Найдём среднее арифметическое из этих равенств

.

Следовательно, среднее арифметическое (L₀ и R₀) из диаметрально противоположных отсчётов L и R по лимбу, взятых при визировании на точку местности, свободно от влияния эксцентриситета алидады.

5.1.3 Уровни геодезических приборов

Уровни - части геодезических приборов, которые служат для приведения осей и плоскостей приборов в горизонтальное либо отвесное положение, а также для наблюдения за отдельными частями их во время измерений. По конструкции (см. рис. 5.5 и 5.6) различают уровни цилиндрические и круглые (сферические).

Характеристики уровней.

1. Ось цилиндрического уровня (UU') - касательная к дуге продольного сечения внутренней поверхности ампулы, проведённая в нуль-пункте (рис. 5.5). При положении пузырька уровня в нуль-пункте ось горизонтальна.

2. Ось круглого уровня (UU') - радиус кривизны внутренней (сферической) поверхности крышки ампулы, проходящий через нуль-пункт. При положении пузырька в нуль-пункте ось - отвесна.

3. Цена деления уровня (τ) -центральный угол, опирающийся на дугу внутренней поверхности ампулы, соответствующей одному делению (l) шкалы. Цена делений цилиндрических уровней ≤ 1', круглых >1'.

4. Чувствительность - наименьший угол, на который следует наклонить ось уровня, чтобы пузырёк переместился на едва различимую глазом величину, она составляет ≈ 0,15 τ.

- 70 -

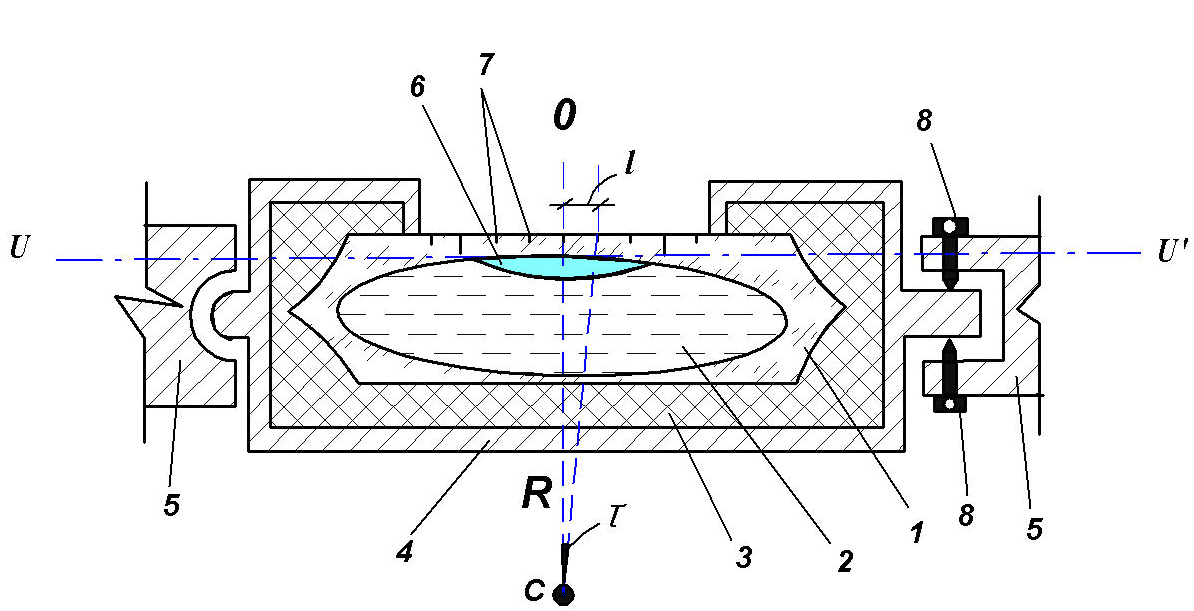Рис. 5.5. Цилиндрический уровень:

1 - ампула, 2 - наполнитель, 3 - гипс, 4 - оправа, 5 - корпус геодезического прибора, 6 - пузырёк уровня (пары наполнителя), 7 - штрихи шкалы ампулы, 8 - исправительные (юстировочные) винты, "0" - нуль-пункт (середина шкалы ампулы), UU' - ось уровня, l - деление шкалы (обычно - 2 мм), τ - цена деления уровня, R - радиус кривизны внутренней (бочкообразной) поверхности ампулы.

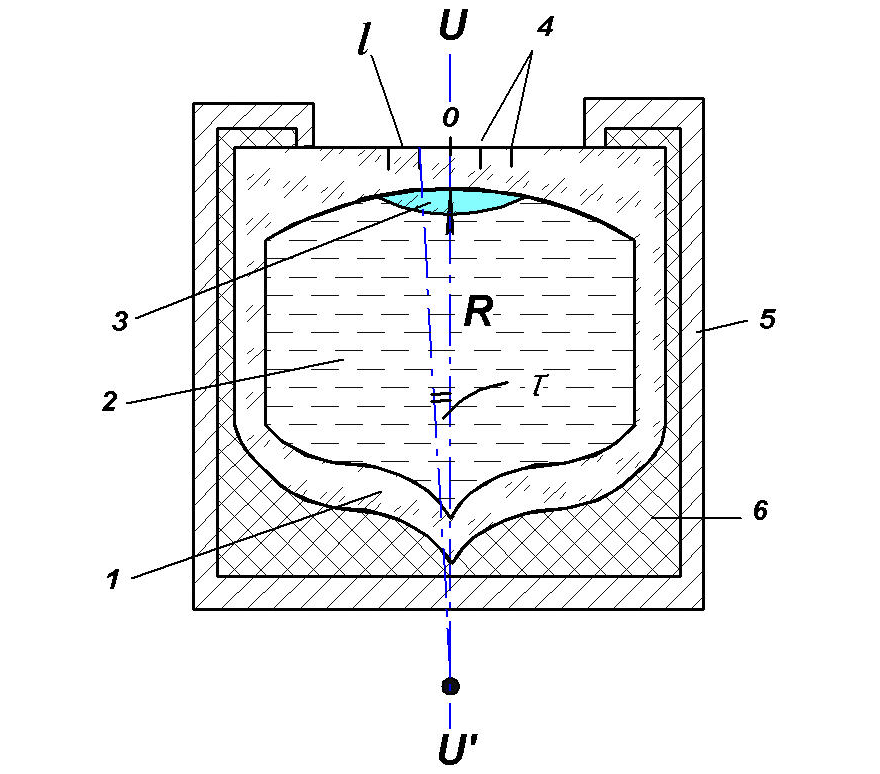
Рис. 5.6.Круглый уровень:

1 - ампула, 2 - наполнитель, 3 - пузырёк, 4 - шкала ампулы (концентрические окружности), 5 - оправа, 6 - гипс, l- деление шкалы, "0" - нуль-пункт (центр концентрических окружностей), UU' - ось уровня, τ - цена деления, R - радиус кривизны внутренней (сферической) поверхности крышки ампулы.

- 71 -