
- •§ 1 Понятие числового ряда.
- •§ 2 Числовые ряды с положительными
- •2. Второй признак сравнения (предельный)
- •3. Признак Даламбера.
- •4. Признак Коши (радикальный)
- •§ 3 Знакопеременные ряды.
- •2. Элементы функциональных рядов.
- •§ 1. Определение функционального ряда
- •§ 2 Степенные ряды.
- •§ 3. Ряд тейлора. Приложения степенных
- •3. Ряды фурье
- •§ 1. Вводные замечания
- •§ 2. Теорема единственности. Ряд фурье.
- •§ 3. Ряд фурье для чётных и нечётных функций.
- •§ 4. Ряд фурье для функции с произвольным
- •§ 5 Ряд фурье в комплексной форме.
- •§ 6. Приложения рядов фурье.
- •1. Задача о колебании струны.
- •§ 7 Преобразование фурье.
- •1 Интеграл Фурье
- •6. Приложения преобразований Фурье.
- •§ 1. Понятие числового ряда ………………………………… 3
3. Ряды фурье
§ 1. Вводные замечания
Мы знаем, какую большую пользу приносит представление функции в форме:
![]() (1)
(1)
т.е.
в форме суммы степенного ряда. Такое
представление даёт возможность и
находить приближённо численные значе-
ния функции, и устанавливать различные
свойства функций, вычислять определённые
интегралы, решать дифференци- альные
уравнения и т.п. Столь плодотворным
представление (1) оказывается потому,
что отдельные слагаемые правой части
являются чрезвычайно простыми
функциями. Можно сказать, что формула
(1) показывает, как составлена сложная
функция
![]() из простейших функций
из простейших функций
![]() (2)
(2)
Таким образом, разложение (1) в некотором роде сходно с разложением многочлена на множители или с разложением рациональной дроби на простые и т.п.
Наряду с системой степеней (2), в элементарной мате- матике хорошо изучена система тригонометрических функций:
![]() (3)
(3)
Поэтому,
кроме представления функции
![]() в форме (1), большое значение имеет
её представление в форме суммы ряда
по функциям (3), т.е. в форме
в форме (1), большое значение имеет
её представление в форме суммы ряда
по функциям (3), т.е. в форме
![]() (4)
(4)
Ряд такого вида называется тригонометрическим рядом.
Напомним важное свойство тригонометрических функций:
![]()
Если
функция
![]() обладает тем свойством, что при неко-
торой постоянной
обладает тем свойством, что при неко-
торой постоянной![]() и всех
и всех![]() оказывается
оказывается
![]() ,
,
то
говорят, что функция
![]() имеет период
имеет период![]() или, короче
или, короче![]() - периодична. Таким образом, все
функции системы (3) яв- ляются
- периодична. Таким образом, все
функции системы (3) яв- ляются![]() - периодичными. Но тогда и сумма ряда
(4) долж- на быть
- периодичными. Но тогда и сумма ряда
(4) долж- на быть![]() - периодичной: если все члены ряда не
меняются от замены
- периодичной: если все члены ряда не
меняются от замены![]() на
на![]() ,
то и сумма ряда не меняется от такой
замены. Поэтому тригонометрические
ряды являются аппаратом, особенно
удобным для представления
,
то и сумма ряда не меняется от такой
замены. Поэтому тригонометрические
ряды являются аппаратом, особенно
удобным для представления![]() - пери -одических функций.
- пери -одических функций.
Ортогональность тригонометрической системы.
ОПРЕДЕЛЕНИЕ.
Две
функции
![]() и
и![]() называютсявзаимно
ортогональными
на промежутке
называютсявзаимно
ортогональными
на промежутке
![]() ,
если
,
если
![]() .
.
ТЕОРЕМА 1. Любые две функции системы
![]() (3)
(3)
взаимно
ортогональны на отрезке
![]() .
.
Доказательство теоремы основано на следующей лемме.
Лемма.
Если
![]() - целое (положительное или отрица-
тельное число), то
- целое (положительное или отрица-
тельное число), то
![]() (5)
(5)
В самом деле,
![]()
Аналогично доказывается и второе из равенств (5).
Переходя к доказательству теоремы, мы должны выбирать из системы (3) различные пары функций и находить интеграл от их произведения. При этом могут представиться следую- щие случаи.
Одна из выбранных функций
 ,
а вторая -
,
а вторая -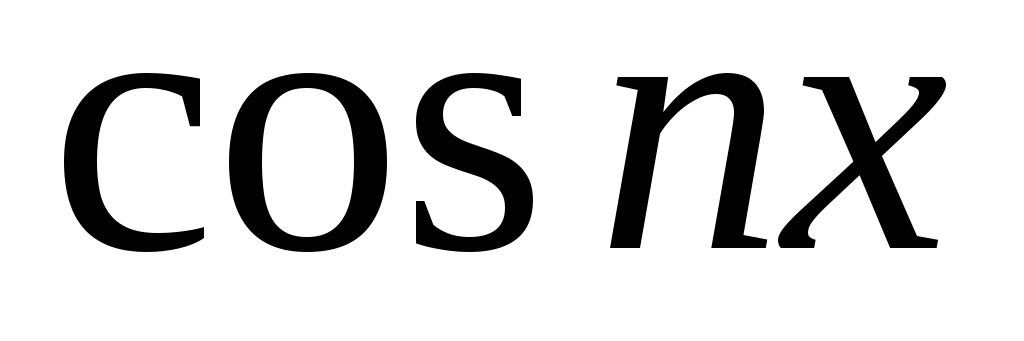 или
или .
Тогда упомянутый интеграл будет
равен нулю, в силу леммы.
.
Тогда упомянутый интеграл будет
равен нулю, в силу леммы.Выбрана пара функций
 и
и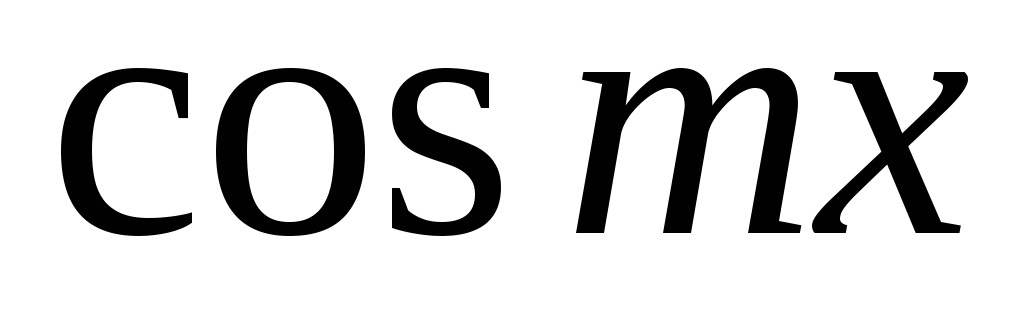 .
Так как
.
Так как
![]() (6)
(6)
тогда

По лемме, оба интеграла, стоящие справа, равны нулю.
3).
Выбраны функции
![]() и
и![]() Тогда вместо (6) нужно применить
формулу:
Тогда вместо (6) нужно применить
формулу:
![]()
и рассуждать, как в 2).
4)
Выбраны функции
![]() и
и![]() .
Так как
.
Так как
![]()
то

По лемме, оба интеграла справа равны нулю.
Итак,
какие бы различные функции из системы
(3) ни взять, интеграл от их произведения
по промежутку
![]() равен нулю. Это и требовалось доказать.
равен нулю. Это и требовалось доказать.
Нам понадобится ещё
ТЕОРЕМА
2. При любом натуральном
![]() будет
будет
![]() .
(7)
.
(7)
В самом деле,
![]() .
.
Отсюда

Аналогично доказывается и второе равенство из (7).
