
- •§ 1 Понятие числового ряда.
- •§ 2 Числовые ряды с положительными
- •2. Второй признак сравнения (предельный)
- •3. Признак Даламбера.
- •4. Признак Коши (радикальный)
- •§ 3 Знакопеременные ряды.
- •2. Элементы функциональных рядов.
- •§ 1. Определение функционального ряда
- •§ 2 Степенные ряды.
- •§ 3. Ряд тейлора. Приложения степенных
- •3. Ряды фурье
- •§ 1. Вводные замечания
- •§ 2. Теорема единственности. Ряд фурье.
- •§ 3. Ряд фурье для чётных и нечётных функций.
- •§ 4. Ряд фурье для функции с произвольным
- •§ 5 Ряд фурье в комплексной форме.
- •§ 6. Приложения рядов фурье.
- •1. Задача о колебании струны.
- •§ 7 Преобразование фурье.
- •1 Интеграл Фурье
- •6. Приложения преобразований Фурье.
- •§ 1. Понятие числового ряда ………………………………… 3
2. Второй признак сравнения (предельный)
ТЕОРЕМА
3. Пусть даны два ряда со строго
положи- тельными членами
![]() (1) и
(1) и![]() (2), для элементов которых выполняется
условие:
(2), для элементов которых выполняется
условие:
![]() .
(7)
.
(7)
Тогда ряды (1) и (2) ведут себя одинаково, т.е. сходятся и
расходятся одновременно.
В
самом деле, из определения предела
следует, что для любого
![]() найдётся номер
найдётся номер![]() ,
начиная с которого (т.е. для всех
,
начиная с которого (т.е. для всех![]() )
выполняется неравенство
)
выполняется неравенство
![]() ,
,
Отсюда,
![]() .
.
Учитывая замечание 2 из предыдущей теоремы, из сходимости ряда (2), по неравенству (6), следует сходимость ряда (1), и наоборот, из расходимости ряда (1) следует расходимость ряда (2).
В
частности, если
![]() ,
то равенство (7) означает экви -лентность
рядов (1) и (2) (
,
то равенство (7) означает экви -лентность
рядов (1) и (2) (![]() ~
~![]() ).
).
Рассмотрим примеры. Исследовать на сходимость ряды:
1.
![]() .
Общий член этого ряда
.
Общий член этого ряда
![]() ~
~ при
при
![]() .
.
Тогда
![]() .
Ряд
.
Ряд
 расходится, как
расходится, как
обобщённый
гармонический ряд с
![]() .
Тогда расходится и исходный ряд.
.
Тогда расходится и исходный ряд.
2.
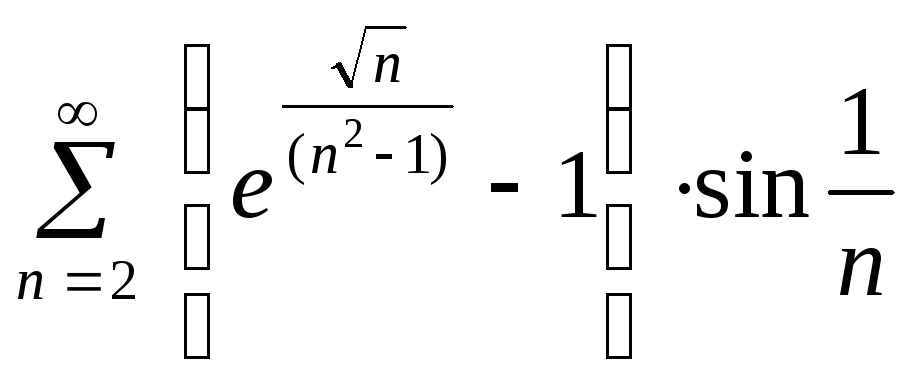 .
Для данного ряда, применяя таб- лицу
эквивалентных бесконечно малых
функций, получим:
.
Для данного ряда, применяя таб- лицу
эквивалентных бесконечно малых
функций, получим:
 ~
~
![]() ~
~![]() ~
~![]() .
.
Ряд
![]() сходится, так как
сходится, так как
![]() ,
следо- вательно исходный ряд также
сходится, так как предел отно- шения
общих членов этих рядов равен 1 (т.к.
они эквивалент- ны).
,
следо- вательно исходный ряд также
сходится, так как предел отно- шения
общих членов этих рядов равен 1 (т.к.
они эквивалент- ны).
3. Признак Даламбера.
Пусть
для элементов ряда
![]() (1) выполняется условие:
(1) выполняется условие:
![]() .
(8)
.
(8)
Тогда,
если
![]() ,
то ряд (1) сходится; если
,
то ряд (1) сходится; если![]() ,
то ряд (1) расходится; если
,
то ряд (1) расходится; если![]() ,
то данный признак не даёт ответа на
вопрос о сходимости ряда.
,
то данный признак не даёт ответа на
вопрос о сходимости ряда.
В
самом деле, из определения предела
следует, что для любого
![]() найдётся номер
найдётся номер![]() ,
начиная с которого (т.е. для всех
,
начиная с которого (т.е. для всех![]() )
выполняется неравенство:
)
выполняется неравенство:![]() ,
или, что то же самое
,
или, что то же самое
![]() .
(9)
.
(9)
Пусть
![]() .
Выберем
.
Выберем![]() так, чтобы
так, чтобы![]() .
Тогда
.
Тогда
из
правой части неравенства (9), получаем
![]() ,
или
,
или![]() Таким
образом, получаем следующее неравенство:
Таким
образом, получаем следующее неравенство:
![]() ,
которое выполняется для всех
,
которое выполняется для всех
![]() .
.
Ряд,
стоящий справа, представляет собой
сумму сходящей- ся геометрической
прогрессии (![]() ).
Тогда, по первому при- знаку сравнения,
ряд, стоящий в левой части неравенства,
также сходится. По следствию 3 из
предыдущего параграфа, получаем
сходимость ряда (1).
).
Тогда, по первому при- знаку сравнения,
ряд, стоящий в левой части неравенства,
также сходится. По следствию 3 из
предыдущего параграфа, получаем
сходимость ряда (1).
Пусть
![]() .
Выберем
.
Выберем![]() так, чтобы
так, чтобы![]() .
Тогда
.
Тогда![]() ,
т.е., начиная с номера
,
т.е., начиная с номера![]() ,
члены ряда (1) образуют возрастающую
последовательность и не выполняется
необходимый признак сходимости рядов.
,
члены ряда (1) образуют возрастающую
последовательность и не выполняется
необходимый признак сходимости рядов.
Поэтому ряд (1) расходится.
ПРИМЕРЫ. Исследовать на сходимость ряды:
1.
![]() .
.![]() ,
,![]() .
.
Тогда получаем:
![]() .
.
По признаку Даламбера, ряд сходится.
2.
![]() .
Для данного ряда
.
Для данного ряда![]() .
Тогда
.
Тогда![]() .
.
Применим признак Даламбера:
![]()
(степень числителя меньше степени знаменателя). Поэтому ряд сходится.
3.
![]() .
Здесь
.
Здесь![]() ,
следователь- но
,
следователь- но![]() .
После сокра-
.
После сокра-
щения,
получаем:
![]()
(степень числителя больше степени знаменателя). Следова – тельно данный ряд расходится.
Замечание.
Признаком Даламбера удобно пользоваться
в случае, если общий член ряда
содержит
![]() -
ые степени, фак – ториалы, бесконечные
произведения.
-
ые степени, фак – ториалы, бесконечные
произведения.
