
- •1. Определение численности выборки при организации выборочного наблюдения
- •2. Определение ошибки выборочной средней и доли
- •Живая масса и пол цыплят
- •Многоплодие свиноматок и доля мертворожденных поросят
- •Суточный удой коровы
- •Поголовье коров и число ферм на сельскохозяйственных предприятиях
- •3. Определение вероятности осуществления заданной ошибки
Практическое занятие 4
ВЫБОРОЧНЫЙ МЕТОД
1. Определение численности выборки при организации выборочного наблюдения 1
2. Определение ошибки выборочной средней и доли 7
3. Определение вероятности осуществления заданной ошибки 29
1. Определение численности выборки при организации выборочного наблюдения
При подготовке к выборочному наблюдению, прежде всего, необходимо определить численность выборки. Число единиц в выборочной совокупности должно быть такое, чтобы ошибка выборки не превышала заданные размеры при определенном уровне вероятности суждения.
Исходя из формул, приведенных выше, для определения численности выборки необходимо знать нормированное отклонение при соответствующем уровне вероятности суждения, предельно допустимую ошибку и дисперсию выборочной совокупности.
Первые два показателя задают произвольно. По таблицам интеграла вероятности в соответствии с уровнем вероятности суждения определяют нормированное отклонение. Предельную ошибку задают в зависимости от целей исследования.
Затруднение обычно возникает при определении дисперсии выборочной совокупности, так как она неизвестна и будет определена лишь после выборочного обследования. Вместо фактического значения дисперсии определяют приближенное значение на основании предварительной оценки или данных предыдущих наблюдений.
Рассмотрим методику определения численности выборки при различных способах отбора.
Пример 1. Для анализа живой массы цыплят на птицефабрике предполагается провести случайный повторный отбор. Требуется определить численность выборки, чтобы с вероятностью 0,95 можно было гарантировать размер ошибки выборки не более 3,5 г. По предварительной оценке колеблемость живой массы не превышает 9 г. Требуется также определить, какая должна быть численность выборки, чтобы в нее поровну вошли петушки и курочки, и ошибка не превысила 5 %.
Вначале с помощью таблицы «Значения интеграла вероятностей при разных значениях t» определим значение нормированного отклонения при уровне вероятности суждения 0,95. Оно равно 1,96.
Подставляя исходные данные в формулы для случайного повторного отбора определим необходимую численность выборки:
для живой массы цыплят:
![]() ;
;
для доли петушков и курочек:
![]() .
.
Таким образом, для того, чтобы гарантировать заданные ошибки с вероятностью 0,95, в первом случае необходимо сделать выборку в 25 единиц, а во втором в 384 единицы.
Технология решения задачи в табличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 4.1.

Р и с. 4.1
2. Рассчитайте среднее квадратическое отклонение для доли петушков и курочек. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,5*(1-0,5)).
3. Рассчитайте численность выборки для живой массы цыплят и доли петушков и курочек.
3.1. Введите в ячейку В6 формулу =B3^2*B4^2/B5^2.
3.2. Скопируйте ячейку В6 в ячейку С6.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.2).

Р и с. 4.2
Пример 2. Для анализа многоплодия 600 свиноматок на комплексе требуется провести случайный бесповторный отбор. Для этого надо определить, какое поголовье их учесть, чтобы при вероятности 0,95 ошибка выборки не превысила 0,6 поросенка. Необходимо также определить какая должна быть выборка, чтобы, при том же уровне вероятности суждения ошибка средней доли мертворожденных поросят была не более 0,08. Предварительные исследования показали, что колеблемость многоплодия свиноматок не превышает 1,6 гол., а доля мертворожденных поросят составляет около 6 %.
С помощью таблицы «Значения интеграла вероятностей при разных значениях t» определяем, что нормированное отклонение при уровне вероятности суждения 0,95 равно 1,96.
Численности выборок для случайного бесповторного отбора будут равны:
для среднего многоплодия свиноматок:
![]() ;
;
для доли мертворожденных поросят:
![]() .
.
Для того чтобы гарантировать заданные ошибки с вероятностью 0,95, в первом случае необходимо сделать выборку в 26 единиц, а во втором 32.
Технология решения задачи в табличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 4.3.

Р и с. 4.3
2. Рассчитайте среднее квадратическое отклонение для доли мертворожденных поросят. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,06*(1-0,06)).
3. Рассчитайте численность выборки для многоплодия свиноматок и доли мертворожденных поросят.
3.1. Введите в ячейку В7 формулу =B3^2*B4^2*B6/(B3^2*B4^2+B5^2*(B6-1)).
3.2. Скопируйте ячейку В7 в ячейку С7.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.4).

Р и с. 4.4
Пример 3. Для анализа продуктивности коров различной породности необходимо сделать выборку. Требуется определить ее численность, если известно, что в стаде 625 голов, средняя колеблемость суточного удоя молока в группах различной породности составляет около 2,5 кг, а ошибка выборки в среднем не должна превышать 0,9 кг. Определить также, какая необходима выборка, чтобы в нее поровну вошли коровы с суточным удоем молока выше и ниже среднего уровня (20,1 кг). При этом в среднем ошибка выборки не должна превышать 20 %. Уровень вероятности суждения 0,95.
Нормированное отклонение при уровне вероятности суждения 0,95 равно 1,96 (таблица «Значения интеграла вероятностей при разных значениях t»).
Поскольку в стаде выделены группы коров с различной породностью, то численность выборки следует определять по формулам для типического отбора. Численность выборок будет:
для суточной продуктивности коров:
 ;
;
для доли коров с удоем выше и ниже среднего:
![]() .
.
Таким образом, для того, чтобы гарантировать заданные ошибки с вероятностью 0,95, в первом случае необходимо сделать выборку в 28 единиц, а во втором — в 23 единицы.
Технология решения задачи в табличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 4.5.
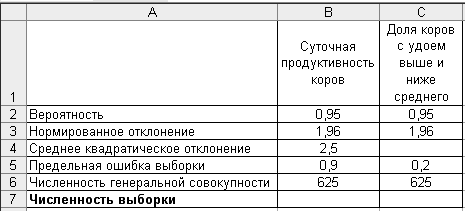
Р и с. 4.5
2. Рассчитайте среднее квадратическое отклонение для доли коров с удоем выше и ниже среднего. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,5*(1-0,5)).
3. Рассчитайте численность выборки для суточной продуктивности и доли коров с удоем выше и ниже среднего.
3.1. Введите в ячейку В7 формулу =B3^2*B4^2*B6/(B3^2*B4^2+B5^2*(B6-1)).
3.2. Скопируйте ячейку В7 в ячейку С7.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.6).

Р и с. 4.6
Пример 4. Для характеристики ферм с беспривязным содержанием коров, необходимо сделать выборку по 96 сельскохозяйственным предприятиям. Требуется определить, сколько хозяйств должно быть в выборке, если известно, что поголовье коров на ферме изменяется в пределах 25 гол., а доля ферм с беспривязным содержанием коров составляет примерно 60 % от всех ферм. Ошибка среднего поголовья коров не должна превышать 8 гол., а ошибка доли ферм с беспривязным содержанием коров 17 % при уровне вероятности суждения 0,9.
Нормированное отклонение при уровне вероятности суждения 0,9 равно 1,6449 (таблица «Значения интеграла вероятностей при разных значениях t»).
В данном случае выборку производят способом серийного отбора, так как каждое хозяйство представляет серию объектов, то есть ферм с беспривязным содержанием коров. Расчеты следует проводить по формулам для серийного отбора. Численность выборки будет:
для среднего поголовья коров с беспривязным содержанием:
 ;
;
для доли ферм с беспривязным содержанием коров:

Таким образом, для того, чтобы гарантировать заданные ошибки с вероятностью 0,9, в первом случае необходимо сделать выборку в 21 серию (сельскохозяйственное предприятие), а во втором в 18 серий.
Технология решения задачи в табличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 4.7.

Р и с. 4.7
2. Рассчитайте среднее квадратическое отклонение доли ферм с беспривязным содержанием коров. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,6*(1-0,6)).
3. Рассчитайте численность выборки для среднего поголовья коров и доли звеньев с беспривязным содержанием.
3.1. Введите в ячейку В7 формулу =B3^2*B4^2*B6/(B3^2*B4^2+B5^2*(B6-1)).
3.2. Скопируйте ячейку В7 в ячейку С7.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.8).

Р и с. 4.8
