
- •Практическое занятие 2 расчет средних величин
- •1. Средняя арифметическая
- •Удой коровы
- •Поголовье коров и удой молока
- •2. Средняя гармоническая
- •Затраты на производство молока
- •3. Средняя геометрическая
- •Т а б л и ц а 2.4 Коэффициенты роста поголовья крупного рогатого скота
- •4. Средняя квадратическая
- •Длина шкурок кролика
- •Т а б л и ц а 2.6 Диаметр сосков вымени у коровы
- •5. Мода и медиана
- •Приплод норок
2. Средняя гармоническая
Средняя гармоническая является обратной величиной средней арифметической, рассчитанной из обратных значений признака. В качестве частот в этом случае используются не единицы совокупности, а произведения этих единиц на значения признака.
Среднюю гармоническую применяют в тех случаях, когда известны индивидуальные значения и объемы признака, а частоты неизвестны.
Формула средней гармонической имеет вид:
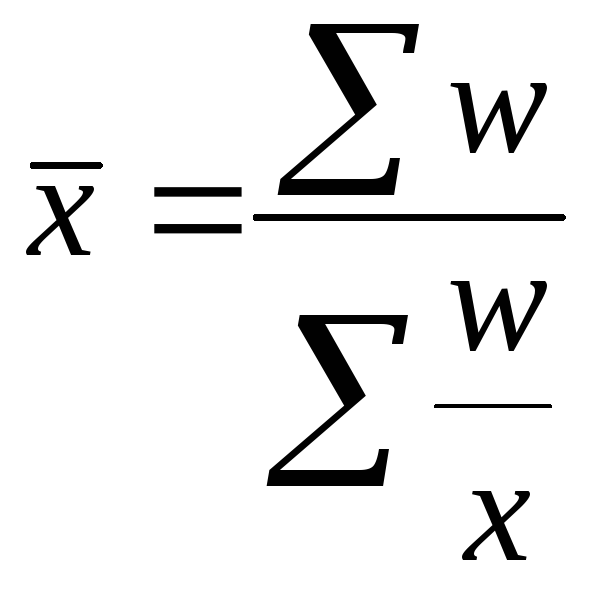 ,
,
где
![]()
средняя;
средняя;
х варианты;
w объемы явления.
Рассмотрим методику расчета средней гармонической.
Пример. Имеются данные по сельскохозяйственным предприятиям об общих затратах на производство молока и себестоимости 1 ц (табл. 2.3).
Т а б л и ц а 2.3
Затраты на производство молока
|
Предприятие |
Затраты на производство молока, руб. |
Себестоимость 1 ц молока, руб. |
Производство молока, ц |
|
w |
x |
| |
|
1 |
698261 |
424 |
1647 |
|
2 |
964854 |
435 |
2218 |
|
3 |
1063853 |
398 |
2673 |
|
4 |
965840 |
415 |
2327 |
|
5 |
568865 |
567 |
1003 |
|
6 |
1858349 |
458 |
4058 |
|
7 |
879621 |
437 |
2013 |
|
8 |
1222147 |
520 |
2350 |
|
Итого |
|
|
|
Требуется определить среднюю себестоимость 1 ц молока по всем предприятиям.
Для расчета средней необходимо определить общее производство молока по всем предприятиям и затраты на его производство. Средняя себестоимость 1 ц молока будет рассчитываться по формуле средней гармонической:
 руб.
руб.
Средняя себестоимость 1 ц молока по всем сельскохозяйственным предприятиям составляет 450 руб.
Технология решения задачи в табличном процессоре Microsoft Excel следующая.
1. Введите исходные данные в соответствии с рис. 2.9.

Р и с. 2.9
2. Рассчитайте производство молока по предприятиям.
2.1. Введите в ячейку D2 формулу =В2/С2.
2.2. Скопируйте ячейку D2 в ячейки D3:D9.
3. Рассчитайте общие затраты на производство молока.
3.1. Выделите ячейку Е11.
3.2.
Щелкните левой кнопкой мыши на панели
инструментов на букве
кнопки <Автосумма >
![]() .
.
3.3. Выделите ячейки В2:В9.
3.4. Нажмите клавишу <Enter>.
4. Рассчитайте общее производство молока. Для этого вставьте в ячейку Е12 математическую функцию =СУММ(D2:D9). Порядок расчетов изложен в пункте 3.
5. Рассчитайте среднюю себестоимость 1 ц молока как среднюю гармоническую. Для этого введите в ячейку Е13 формулу =E11/E12.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 2.10).

Р и с. 2.10
3. Средняя геометрическая
Средняя геометрическая — это средняя, в которой общий объем явления представляет произведение индивидуальных значений признака. Такую среднюю применяют в основном для расчета среднего темпа изменения какого-либо показателя за определенный промежуток времени.
Формула расчета средней геометрической имеет вид:
![]() ,
,
где
![]()
средняя;
средняя;
х варианты;
n число вариант;
П — произведение.
Рассмотрим методику расчета средней геометрической.
Пример. Имеются данные об ежегодных темпах изменения поголовья крупного рогатого скота на сельскохозяйственном предприятии (табл. 2.4).
