
Математика / По темам шпаргалки / 3. Шпаргалка по первообразным — подборка шпаргалок по математике
.pdf
Первообразная, F(x) |
Функция, f(x) |
Производная, f'(x) |
||||||||||
Ax + C, A R |
|
A (const), A R |
|
|
0 |
|||||||
|
kx2 |
bx C |
|
kx + b, k R, b R |
|
k, k R |
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
C |
|
|
x² |
|
|
2x |
|||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
x4 |
C |
|
|
x³ |
|
|
3x² |
|||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
xn 1 |
C |
|
|
xn , n N |
nx n 1 , n N |
|||||
|
|
n |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
ln|x|+C |
|
|
1 |
|
|
1 |
||||
|
|
|
|
x |
|
|
|
x2 |
||||
|
1 |
|
|
|
C , n N |
1 , n N |
|
n |
, n N |
|||
( n 1)xn 1 |
|
|
|
xn |
|
xn 1 |
|
|||||
n |
|
n 1 |
|
|
|
|
|
|
1 |
|
|
|
n x |
|
|
C , n N |
n x , n N |
|
|
|
, n N |
||||
n 1 |
|
|
|
|
|
|
nn xn 1 |
|||||
|
2 x |
x C |
|
|
x |
|
|
1 |
||||
|
3 |
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
2 |
x + C |
|
|
1 |
|
|
|
1 |
||
|
|
|
|
x |
|
2x x |
||||||
|
|
|
|
|
|
|
|
|
|
|||
xα 1 |
C , α R, α ≠ –1 |
xα , α R |
αxα 1 , α R |
|||||||||
α 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− cos x + C |
|
|
sin x |
|
|
cos x |
|||||
|
|
sin x + C |
|
|
cos x |
|
− sin x |
|||||
− ln(cos x) + C |
|
tg x |
|
|
1 |
|||||||
|
|
cos2 x |
||||||||||
|
ln(sin x) + C |
|
ctg x |
|
|
|
1 |
|||||
|
|
|
sin2 x |
|||||||||
|
|
|
|
|||||||||
1 x 1 sin 2x C |
cos²x |
|
− sin 2x |
|||||||||
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
1 x 1 sin 2x C |
sin²x |
|
sin 2x |
|||||||||
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
e x + C |
|
|
e x |
|
|
e x |
|||
|
|
ax |
C |
|
|
ax |
|
ax ln a |
||||
|
|
|
|
|
|
|
||||||
|
|
ln a |
|
|
|
|
|
|
|
|
||
|
xln x − x + C |
|
ln x |
|
|
1 |
||||||
|
|
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
1 (x ln x x) C |
|
loga x |
|
|
1 |
|||||||
ln a |
|
|
|
|
|
|
|
|
|
|
x ln a |
|
x arcsin x + |
|
1 x |
2 |
+ C |
arcsin x |
|
|
1 |
||||
|
|
|
|
|
||||||||
|
|
|
|
1 x2 |
||||||||
|
|
|
|
|
||||||||
x arccos x − |
|
1 x |
2 |
+ C |
arccos x |
|
− |
|
1 |
|||
|
|
|
|
|||||||||
|
|
|
1 |
x2 |
||||||||
|
|
|
|
|
||||||||
x arctg x − 1 ln(1 + x²) + C |
arctg x |
|
|
1 |
||||||||
|
|
2 |
|
|
|
|
|
1 x 2 |
||||
|
|
|
1 |
|
|
|
|
|
|
− |
|
1 |
x arcctg x + |
2 ln(1 + x²) + C |
arcctg x |
|
1 x2 |
||||||||
Учитель математики Семёнова Елена Юрьевна МБОУ СОШ №5-«Школа здоровья и развития» г.Радужный |
||||||||||||
|
|
|
|
|
|
|
|
Правила дифференцирования |
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
u |
|
v |
|
; |
|
1 |
|
|
|
|
v |
|
|
|
|
||
u v |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
; |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
2. |
|
C u |
|
; |
|
|
|
v |
|
|
|
|
v |
|
|
|
||||
Сu |
|
|
|
|
|
|
|
|
|
u v u v |
|
|||||||||
|
|
|
|
|
|
|
|
|
u |
|
|
|||||||||
3. |
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
. |
|||
u v |
u v u v ; |
|
|
|
|
v |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
||
Производная сложной функции
h f x h f x f x
Геометрический смысл производной состоит в том, что значение производной функции в точке xо равно угловому коэффициенту касательной (тангенсу угла α), проведенной к графику функции в точке с абсциссой xо.
k f xо tg α
Уравнение касательной к графику функции f(x) в точке с абсциссой хо:
у f xо x xo f xo
Физический смысл производной состоит в том, что производная от координаты по времени есть мгновенная
скорость:
v t s t
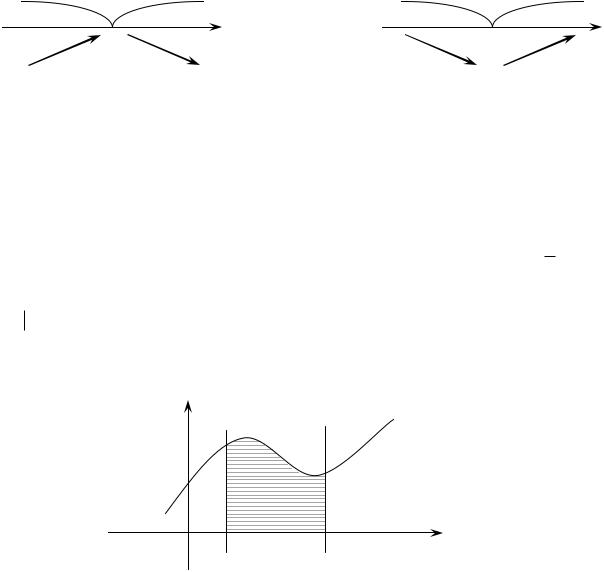
Если в точке хо производная функции f(x) меняет знак с «+» на «−», то хо – точка максимума функции f(x).
Если в точке хо производная функции f(x) меняет знак с «−» на «+», то хо – точка минимума функции f(x).
f x |
+ |
− |
|
− |
+ |
f x |
|||||
f x |
|
хо |
f x |
|
хо |
|
|
|
|
Первообразная. Интеграл
Функцию F(x) называют первообразной для функции f(x) на интервале (a; b), если на нем производная функции F(x) равна f(x): F x f x .
Операцию, обратную дифференцированию называют интегрированием. Три правила нахождения первообразных:
1º Если F(x) есть первообразная для f(x), а G(x) – первообразная для g(x), то F(x) + G(x) есть первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k – постоянная, то функция kF(x) есть первообразная для kf(x).
3º Если F(x) есть первообразная для f(x), а k и b – постоянные, причем k ≠ 0, то функция 1k F(kx + b) есть
первообразная для f(kx + b).
b
f x dx F x ba F b F a – формула Ньютона-Лейбница.
a
Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, образованной линиями: сверху ограниченной кривой у = f(x), и прямыми у = 0; х = a; х = b.
y
y = f(х)
у = 0
0 |
х = а |
х = b |
х |
|
|||
|
|
Учитель математики Семёнова Елена Юрьевна МБОУ СОШ №5-«Школа здоровья и развития» г.Радужный
