
11 класс
Ôàêò 6.
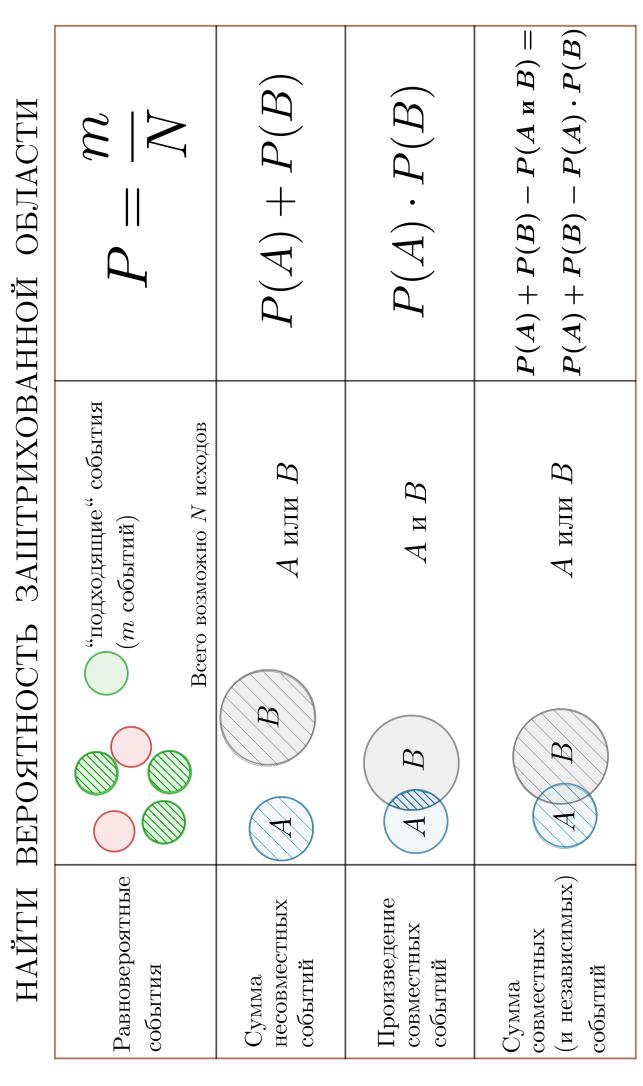
Будем называть два события независимыми, если наступление одного события никак не влияет на наступление другого события. Например, события при бросании кубика выпадет 4 очка и при бросании кубика выпадет 3 очка будут независимыми.
А вот события сломался компьютер и у компьютера перестала работать клавиатура являются зависимыми, потому что то, что именно сломалось в компьютере, напрямую влияет на наступление второго события.
Давайте рассмотрим независимые события. Представим, что у нас есть два совместных события, и нам нужно найти вероятность того, что наступит хотя бы одно из них (до этого мы искали вероятность того, что такие два события наступят одновременно).
Например, подбрасывается игральная кость. Таня сказала: Выпадет 5 или 6! Коля сказал: Выпадет четное число! Найдите вероятность того, что хотя бы один из них окажется прав.
Эту задачу можно решить и старыми методами, поэтому мы так и сделаем, а затем решим ее, используя новый факт, о котором мы скажем дальше. Сколько всего исходов может быть при подбрасывании кубика? Шесть. Теперь давайте определим, сколько из них нам подходит. Чтобы была права Таня, нужно, чтобы выпало 5 или выпало 6 (два исхода). Чтобы был прав Коля, нужно, чтобы выпало 2, или 4, или 6 (три исхода).
(Видим, что эти события пересекаются по событию выпадет 6 .)
Таким образом, если выпадет или 2, или 4, или 5, или 6, то кто-то из ребят
точно будет прав. Значит, нам подходит всего 4 исхода. Следовательно, вероятность равна 46 = 23.
Как решить эту задачу по-другому?
11
11 класс
Верен следующий факт:
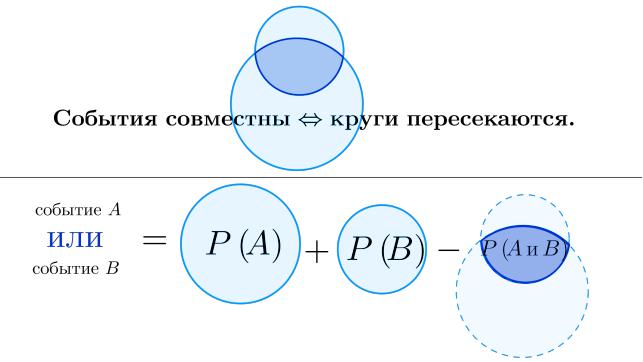
Если для выполнения события C необходимо выполнение хотя бы одного из совместных (которые могут произойти одновременно) событий A è B (C = fA èëè Bg), то вероятность события C равна сумме вероятностей событий A è B за вычетом вероятности fA è Bg.
Каждое событие можно обозначить в виде круга. Тогда если события совместны, то круги должны пересекаться. Вероятность события C это вероятность попасть в один из кругов (то есть попасть хотя бы в один из них).
Комментарий: если просто сложить P (A)+P (B), то получится, что мы
два раза посчитали P (A и B). Именно поэтому один раз вычитается P (A
è B).
12

11 класс
Вернемся к предыдущей задаче. Для того, чтобы воспользоваться данной формулой, нам нужно найти вероятность того, что окажется права Таня, вероятность того, что окажется прав Коля, а также вероятность того, что они
оба окажутся правы.
Вероятность того, что выпадет 5 или 6, равна 26 = 13. Вероятность того, что выпадет четное число, равна 36 = 12.
Вероятность того, что окажутся правы оба это вероятность того, что выпадет 6, то есть 1
6.
Следовательно, искомая вероятность равна
13 + 12 16 = 23
Да, поиск вероятности таким способом для данной задачи не назовешь оптимальным, но мы хотели продемонстрировать вам применение изуча- емого факта.
Разберем еще одну задачу из ЕГЭ по математике, в которой требуется знание данного факта.
Пример.
По мишени по одному разу стреляют два стрелка. Вероятность попадания первого стрелка в мишень равна 0; 7, второго 0; 8. Какова вероятность того, что кто-нибудь из них попадет в мишень?
Решение. В задаче нужно найти вероятность того, чтобы хотя бы один из стрелков попадет в мишень. Очевидно, что события независимые и совместные (ведь то, что первый стрелок попадет в мишень никак не отменяет того, что и второй стрелок может попасть в мишень).
Следовательно, вероятность одновременного наступления этих событий равна 0; 7 0; 8.
Назовем A = fпервый стрелок попал в мишеньg, B = fвторой стрелок попал в мишеньg. Тогда A и B = fпервый стрелок попал в мишень и второй стрелок попал в мишеньg.
Следовательно, вероятность искомого события равна
P(A) + P(B) P(A è B) = 0; 7 + 0; 8 0; 7 0; 8 = 0; 94
13
11 класс
14
