

11 класс
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Ôàêò 1.
Случайное событие это событие, которое при данных условиях может произойти, а может не произойти.
Например, событие при бросании игральной кости выпало 3 или 4 очка . Напомним, что игральная кость это кубик с шестью гранями, на которых написаны числа от 1 до 6.
Предположим, что мы проводим некоторое испытание (эксперимент), например, бросаем игральную кость. Результатом нашего испытания может
быть одно из шести событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков. Такие события называются элементарными событи-
ÿìè (то есть это простейшие события, которые в совокупности образуют все множество исходов нашего эксперимента).
Например, событие при бросании игральной кости выпало 3 или 4 очка не является элементарным, оно состоит из двух элементарных событий при бросании игральной кости выпало 3 очка и при бросании игральной кости
выпало 4 очка .
Если сложить вероятности всех возможных элементарных событий у некоторого эксперимента, то получится 1.
Два события мы будем называть равновероятными (равновозможными), если вероятности наступления любого из них одинаковы. Например, при бросании игральной кости вероятности любого из событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, одинаковы. Или, например, при подбрасывании монеты вероятности событий выпадет орел и выпадет решка также одинаковы.
Примером неравновероятных событий могут послужить два события: при бросании игральной кости выпадет 1 очко и при бросании игральной кости выпадет нечетное количество очков . Почему? В первом случае нам удовлетворяет только исход, когда кубик упадет кверху гранью, на которой написано 1; во втором случае нам подходит целых три исхода: он может выпасть кверху гранью с 1, с 3 или с 5.
1

11 класс
Ôàêò 2.
Если при проведении некоторого эксперимента возможны N равновероят-
ных элементарных событий, то вероятность события A :
P(A) = Nm;
где m количество подходящих элементарных событий.
Вероятность обозначается буквой P.
На рисунке схематично изображено множество всех возможных равновероятных (одинаковые по размеру круги) исходов у некоторого эксперимента, которые не пересекаются:
Таким образом, под такой вероятностью можно понимать часть, которую составляют подходящие исходы от всех возможных исходов.
Давайте рассмотрим несколько примеров, в которых используется данная формула.
2

11 класс
Пример 1.
Найдите вероятность того, что при бросании игральной кости выпадет 3 очка.
Решение. Всего при бросании игральной кости возможны шесть исходов (в данном случае, элементарные события), которые мы описывали ранее. Как мы уже говорили, вероятности наступления каждого из этих исходов одинаковы. Следовательно, N = 6. Подходит нам только один исход: когда выпадет
3 очка. Следовательно, m = 1.
Таким образом, вероятность нашего события равна 16.
Вообще говоря, вероятность любого из исходов: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, равна 1
6.
Пример 2.
Найдите вероятность того, что при бросании двух игральных костей в сумме выпадет 4 очка.
Решение. Для начала нужно найти количество всех возможных исходов у нашего эксперимента. Предположим, на первом кубике выпало 1. Тогда на втором кубике может выпасть 1, 2, 3, 4, 5 или 6. То есть уже есть шесть возможных исходов.
Если на первом кубике выпало 2, то на втором также может выпасть 1, 2, 3, 4, 5 или 6. То есть еще шесть исходов.
Рассуждая аналогично, мы получим шесть блоков по шесть исходов. То есть всего у нашего события 36 возможных исходов (в данном случае, они будут элементарными событиями).
На самом деле, если мы бросаем k игральных костей, то всего у такого экс- перимента будет 6k элементарных исходов.
Теперь давайте подумаем, сколько из них нам подходит. Чтобы в сумме на обоих кубиках было 4 очка, нужно, чтобы:
на первом кубике выпало 1, на втором 3 очка;
на первом кубике выпало 2, а на втором 2 очка;
на первом кубике выпало 3, а на втором 1 очко. Таким образом, нам подходит только три исхода.
Следовательно, вероятность равна 363 = 121 .
3

11 класс
Пример 3.
Торт разделен на 9 кусков, которые условно пронумерованы числами от 1 до 9. Найдите вероятность того, что Маша возьмет кусок с номером 6.
Решение. Маша может взять любой из девяти кусков, следовательно, у нашего эксперимента всего девять исходов. Подходящий нам исход только одинМаша должна взять кусок с номером 6.
Следовательно, вероятность равна 19.
Пример 4.
В соревнованиях по толканию ядра участвуют 8 спортсменов из Аргентины, 6 спортсменов из Бразилии, 5 спортсменов из Парагвая и 6 - из Уругвая. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Аргентины.
Решение. Заметим, что вероятность того, что спортсмен, выступающий последним, окажется из Аргентины, такая же, как вероятность, что он будет выступать первым, вторым, третьим и т.п. Всего претендентов на последнее место 8 + 6 + 5 + 6 = 25 спортсменов. Нам удовлетворяют лишь 8 из Арген-
òèíû.
Следовательно, вероятность равна отношению количества удовлетворяющих исходов к количеству всех: 258 .
4
11 класс
Ôàêò 3.
Если два события в заданных условиях могут происходить одновременно, то их называют совместными. Те, которые происходить одновременно не могут, называют соответственно несовместными.
Например, события при бросании кубика выпадет 3 очка и при бросании кубика выпадет нечетное число очков являются совместными, потому что 3 нечетное число. А вот события при бросании кубика выпадет 3 очка и при бросании кубика выпадет 5 очков будут несовместными, потому что одновременно выпасть и 3 очка, и 5 очков не может.
Также примером совместных событий могут служить события выбранному ученику 13 лет и выбранному ученику не менее 10 лет , которые являются исходами эксперимента: из класса, состоящего из 25 человек, выбирают слу- чайным образом одного ученика.
Еще один пример несовместных событий: играя в шахматы с Машей, Таня выиграла и играя в шахматы с Таней, Маша выиграла .
Все элементарные события являются несовместными (просто в силу своего определения). Любое событие, не являющееся элементарным, есть совокупность некоторого количества элементарных событий. Например, событие при бросании кубика выпадет нечетное число очков есть нечто иное, как совокупность трех событий: при бросании кубика выпадет 1 очко , при бросании кубика выпадет 3 очка и при бросании кубика выпадет 5 очков .
Если назвать событие при бросании кубика выпадет нечетное число очков событием A,
при бросании кубика выпадет 1 очко событием B,при бросании кубика выпадет 3 очка событием C,при бросании кубика выпадет 5 очков событием D, то условно это можно записать так:
A = B [ C [ D èëè A = B èëè C èëè D
5

11 класс
Ôàêò 4.
Верен следующий факт:
Если для выполнения события C необходимо выполнение хотя бы одного из двух несовместных событий A è B (òî åñòü C = fA èëè Bg), то вероятность события C равна сумме вероятностей событий
A è B.
Например, используя предыдущий пример, вероятность события при бросании кубика выпадет нечетное число очков равна сумме вероятностей событий при бросании кубика выпадет 1 очко , при бросании кубика выпа-
дет 3 очка и при бросании кубика выпадет 5 очков . А так как вероятность каждого из этих трех событий равна 1
6, то вероятность событияпри бросании кубика выпадет нечетное число очков равна 16 + 16 + 16 = 12.
Заметим, что если посчитать вероятность этого события, пользуясь фор- мулой P = Nm, то мы получим тот же ответ (естественно ,).
Каждое событие можно обозначить в виде круга. Тогда если события несовместны, то круги не должны пересекаться. Вероятность события C это вероятность попасть в один из кругов.
Таким образом, союз или заменяется на знак + .
6

11 класс
Пример 1.
При подбрасывании игральной кости найти вероятность события C = fвыпадет число, делящееся на три g.
Решение. Можно сказать, что, для того, чтобы выпало число, делящееся на три, нужно, чтобы выпало число 3 или число 6.
Значит, A = fвыпадет 3g, B = fвыпадет 6g, причем эти события несовмест-
íû!
Тогда C = fA или Bg.
Значит, P(C) = P(A) + P(B) = 16 + 16 = 13.
Пример 2.
В небе над домом Никиты в сутки пролетает ровно один самолет. Если разбить сутки на четыре промежутка: утро, день, вечер, ночь, то вероятность того, что Никита увидит в небе самолет утром, равна 0; 45; днем веро-
ятность равна 0; 37; вечером равна 0; 1. Найдите вероятность того, что в
темное время суток (вечером или ночью) Никита из окна своего дома увидит самолет.
Решение. Из условия задачи следует, что вероятность того, что в течение суток Никита увидит самолет, равна 1. Следовательно, вероятность того, что Никита увидит самолет ночью, равна 1 0; 45 0; 37 0; 1 = 0; 08. Следовательно, вероятность того, что Никита увидит самолет в темное время суток, равна 0; 08 + 0; 1 = 0; 18.
Комментарий. В случае совместности событий данная формула уже не верна. Например, при подбрасывании игральной кости найти вероятность
события C ={выпадет четное число}. Ответ должен быть |
P(C) = 1 |
||
|
|
|
2. |
Но если принять за A ={выпадет число, делящееся на |
2}, B ={выпадет |
||
1 |
1 |
1 |
|
число, делящееся на 4}, то P(C) = 2 |
+ 6 |
6=2, потому что события A è B |
|
совместны: они могут произойти одновременно, когда выпадет 4.
Таким образом, прежде чем пользоваться данным фактом, следует убедиться, что события, вероятности которых вы хотите складывать, действительно несовместны!
7

11 класс
Ôàêò 5.
Предположим, что нам нужно найти вероятность некоторого события C, для выполнения которого нужно, чтобы одновременно произошли два события A и B. Чему будет равна такая вероятность?
Для начала следует сказать, что если события A и B являются несовмест-
ными, то вероятность события C будет равна 0. Действительно, ведь несовместные события это события, которые не могут произойти одновременно. А событие C это как раз событие, которое требует одновременного выпол-
нения событий A и B. Очевидно, что такое невозможно. Это и значит, что
вероятность события C равна 0.
Таким образом, мы выяснили, что для того, чтобы вероятность такого события C была ненулевой, события A и B должны быть совместными.
Например, событие C = fпри бросании кубика выпадет 6g можно интерпретировать как C = fA и Bg, где A = fпри бросании кубика выпадет число, делящееся на 3g, B = fпри бросании кубика выпадет число, делящееся на 2g
(потому что из всех чисел 1, 2, 3, 4, 5 или 6 единственное число, делящееся одновременно на 2 и на 3 это 6).
Задача.
Представим, что мы проводим следующий эксперимент. В мешке лежат карандаши двух цветов: черные и красные, а также ручки двух цветов: черные и красные. Причем вероятность достать карандаш равна вероятности достать ручку. Всего карандашей 15, из них 11 черных; ручек всего 35, из них 10 красных. Как нам найти вероятность того, что мы достанем красный карандаш?
Учитывая, что вероятности достать ручку или карандаш одинаковые, то эту задачу можно решить, используя предыдущие факты. Всего предметов в
мешке 50, из них красных карандашей 4 штуки. Значит, вероятность достать красный карандаш равна 504 = 0; 08.
Но эту задачу можно решить и по-другому.
8
11 класс
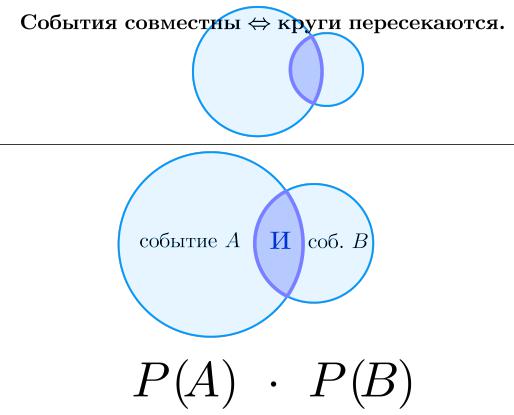
Верен следующий факт:
Если для выполнения события C необходимо выполнение обоих сов-
местных (которые могут произойти одновременно) событий A è B (обозначается это так: C = fA è Bg), то вероятность события C ðàâ-
на произведению вероятностей событий A è B.
Каждое событие можно обозначить в виде круга. Тогда если события совместны, то круги должны пересекаться. Вероятность события C это вероят-
ность попасть в оба круга одновременно (то есть попасть в пересечение этих кругов).
При такой формулировке и видно, что если круги не пересекаются, то попасть в оба круга одновременно невозможно.
Таким образом, союз и заменяется на знак .
9

11 класс
Продемонстрируем данный факт на примере предыдущей задачи.
Пусть событие C = fA и Bg, где A = fдостанем из мешка карандашg, B = fвынутый из мешка карандаш окажется краснымg (видим, что собы-
тия A и B совместны).
Тогда P(C) = P(A) P(B). Вероятность достать из мешка карандаш равна
15
50 (всего 15 карандашей, а предметов в мешке всего 50). Вероятность достать из всех карандашей именно красный равна 4
15 (всего 15 карандашей, из них 4 карандаша красные). Таким образом, искомая вероятность равна
1550 154 = 504 = 0; 08.
Да, поиск вероятности таким способом для данной задачи не назовешь оптимальным, но мы хотели продемонстрировать вам применение изуча- емого факта.
Разберем одну из классических задач ЕГЭ по математике.
Пример.
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0; 5. Если А. играет ч¼рными, то А. выигрывает у Б. с
вероятностью 0; 3. Шахматисты А. и Б. играют две партии, прич¼м во второй
партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение. Наше событие C = fшахматист А. выиграет, играя один раз белыми, и выиграет, играя один раз чернымиg = fA и Bg, где A = fшахматист А. выиграет, играя белымиg, B = fшахматист А. выиграет, играя черными g. Таким образом,
P(C) = P(A) P(B) = 0; 5 0; 3 = 0; 15
Заметим, что если предыдущую задачу про карандаши и ручки мы можем решить, используя разные методы, то данную задачу, не используя изучаемый факт, решить не получится.
10
