
fizika / Магнитное поле соленоида и тороида
.docМагнитное поле соленоида и тороида.
Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник. Тороид можно рассматривать как длинный соленоид, свернутый в кольцо (рис. 4.1).
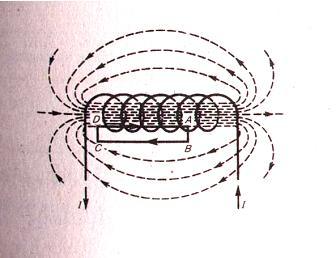
Рис. 4.1. Магнитное поле соленоида
Длина соленоида l содержит N витков и по нему протекает ток I. Считаем соленоид бесконечно длинным. Эксперимент показал, что внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю).
Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, охватывающему все N витков, согласно (4.12) равна:
![]() .
(4.14)
.
(4.14)
Интеграл ![]() можно
представить в виде суммы двух интегралов:
по внутренней части контура:
можно
представить в виде суммы двух интегралов:
по внутренней части контура:![]() и
по внешней:
и
по внешней: ![]() ,
тогда из (4.14) получим:
,
тогда из (4.14) получим:
![]() ,
(4.15)
,
(4.15)
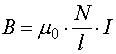 или
или ![]() , (4.16)
, (4.16)
где В –
индукция магнитного поля внутри
соленоида; 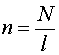 –
число витков на единицу длины соленоида.
–
число витков на единицу длины соленоида.
Магнитное поле внутри тороида, так же, как в соленоиде, однородно, сосредоточено внутри; вне тороида магнитное поле, создаваемое круговыми токами тороида, равно нулю. Величина магнитного поля в тороиде определяется выражением (4.16), причем длина тороида l берется по средней длине тороида (среднему диаметру).
Отметим любопытный факт. Во всех учебниках по физике остался не отмеченным факт существования у соленоида и тороида второго магнитного поля, которое появляется из-за того, что, например, в соленоиде по отношению к средней линии соленоида витки направлены не точно перпендикулярно, а под углом меньше 90°. Это приводит к появлению тока (эффективного, но равного току I, протекающему через соленоид), вдоль соленоида (рис. 4.2).
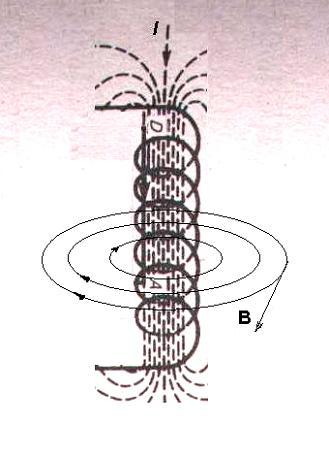
Рис. 4.2. Второе магнитное поле соленоида
То
есть соленоид создает дополнительное
магнитное поле, такое же, как и прямолинейный
бесконечно длинный проводник с током.
Точно так же и для тороида: вдоль средней
линии протекает эффективный ток I.
У
тороида второе магнитное поле эквивалентно
магнитному полю витка с током (рис.4.3).
Диаметр этого витка равен диаметру
тороида (его средней линии), а магнитное
поле тороида 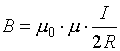 (R –
радиус тороида).
(R –
радиус тороида).
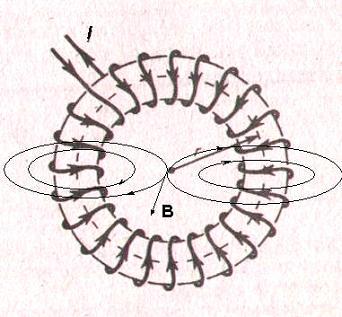
Рис. 4.3. Второе магнитное поле тороида
§ 3. Поток вектора магнитной индукции
Магнитным потоком Ф через площадку S называется скалярная величина
Ф = В ∙ S (4.17)
или
![]() (4.18)
(4.18)
где ![]() –
проекция вектора В на
направление нормали n к
площадке S; –
угол между векторамиВ и n.
–
проекция вектора В на
направление нормали n к
площадке S; –
угол между векторамиВ и n.
Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos. Если рассматривать магнитный поток через контур с током, то положительное направление нормали уже определено правилом правого винта (правило буравчика). Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную этим контуром, всегда положителен. Единица измерения магнитного потока: 1 Вб (Вебер) = 1 Тл 1 м2.
Теорема Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
![]() ,
(4.19)
,
(4.19)
где dS – элемент замкнутой поверхности S, Вn – проекция В на нормаль к этой поверхности.
Эта теорема говорит о том, что в природе отсутствуют магнитные заряды, а линии магнитной индукции замкнуты, то есть магнитное поле является вихревым (соленоидальным).
Магнитный поток через соленоид:
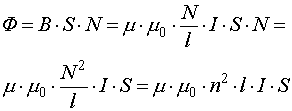 (4.20)
(4.20)
где ![]() .
Отметим, что ВS умножено
на N,
т. е. каждый виток соленоида создает
магнитный поток ВS,
а витков N,
т. е. магнитный поток увеличивается
в N раз.
.
Отметим, что ВS умножено
на N,
т. е. каждый виток соленоида создает
магнитный поток ВS,
а витков N,
т. е. магнитный поток увеличивается
в N раз.
