Теорема Остроградского-Гаусса для электростатического поля в вакууме.

Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхностьинтегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

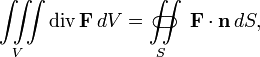
то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму , равен потоку вектора через поверхность , ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:

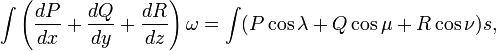
где  и  — дифференциалы объёма и поверхности соответственно. В современной записи  — элемент объёма,  — элемент поверхности.  — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

(2)  Формула (2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀. Эта теорема получена математически для векторного поля произвольной природы русским математиком М.В.Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом.  В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью ρ=dQ/dV, которая различна в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, которая охватывает некоторый объем V,   (3)  Используя формулу (3), теорему Гаусса (2) можно записать так: