fizika / Закон Био-Савара-Лапласа и его применение к расчету магнитного поля

Закон Био-Савара-Лапласа и его применение к расчету магнитного поля.

Основные формулы

     Закон Био-Савара-Лапласа: вектор индукции магнитного поля, созданного элементом проводника , по которому течет ток , имеет вид:

 

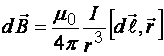 ,                                      (1)

где – радиус-вектор, проведенный от элемента  до той точки, в которой определяется индукция поля;  – магнитная постоянная.

     В скалярной форме

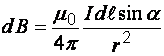,                                             (2)

где – угол между векторами  и .

     Индукция магнитного поля в произвольной точке А, созданного отрезком проводника с током конечной длины,

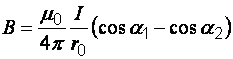,                                (3)

где  – расстояние от т. А до проводника;  – углы, образованные радиус-вектором, проведенном в т.Асоответственно из начала и конца проводника, с направлением тока.

     Магнитная индукция поля в центре кругового тока радиусом R

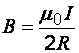.                                                (4)

     Индукция магнитного поля в произвольной т. А, созданного бесконечно длинным прямым проводником с током,

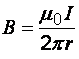,                                                 (5)

где  – расстояние от т. А до проводника.

     Закон полного тока (теорема о циркуляции вектора ): циркуляция вектора  по произвольному замкнутому контуру равна произведению магнитной постоянной  на алгебраическую сумму токов, охватываемых этим контуром

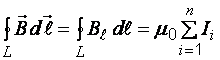,                                    (6)

где  – вектор элементарной длины контура, направленный вдоль обхода контура;  – индукция магнитного поля;  – проекция вектора на направление касательной к контуру;  – угол между векторами  и .

     Магнитная индукция поля внутри соленоида

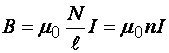,                                       (7)

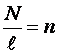где  – магнитная постоянная;  – длина соленоида; – число витков соленоида;  – число витков соленоида на единице его длины.

     Магнитная индукция поля внутри тороида

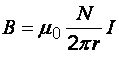,                                           (8)

где  – радиус оси тороида.

     Принцип суперпозиции магнитных полей: магнитная индукция  в любой точке магнитного поля проводника с током равна векторной сумме магнитных индукций , созданных в этой точке всеми элементами  проводника с током, т. е.

,                                            (9)

     Напряженность магнитного поля в вакууме

.
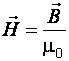