Papka_Vz_dlya_bakalavrov_2014g / Рис. норм. распред

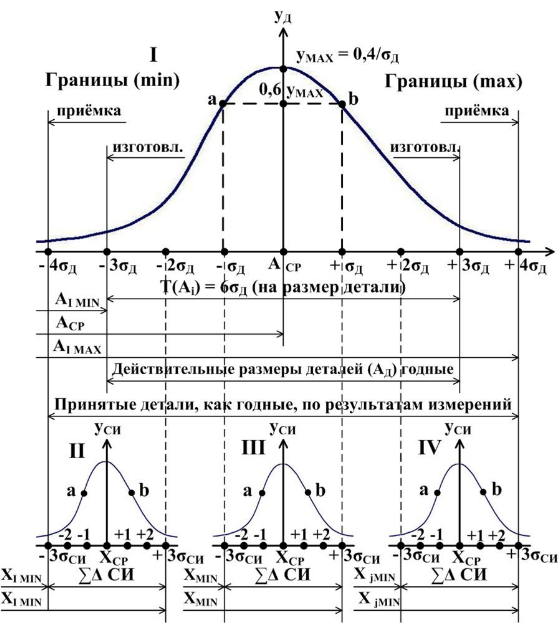
Рисунок - Кривая нормального распределения

I – рассеяние размеров деталей в процессе их обработки

(Ai)действит.;

II, III, IV – рассеяние результатов измерений Xi размеров деталей

(Ai)действит. (II - (Ai)д = Aimin; III - (Ai)д = Aiср.; IV - (Ai)д = Ai max);

a, b – точки перегиба кривых распределений

Как следует из теории вероятностей, кривая нормального распределения

,

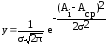A_i – конкретный действительный размер;

А_ср – среднее арифметическое размеров деталей данной партии;

σ – среднее квадратическое отклонение.

,

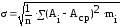где n – количество деталей в партии (n > 1);

m_i – частота (количество деталей данного интервала размеров).

Практический ориентир при выборе СИ для конкретных измерений.

На практике поле рассеяния размеров деталей (допуск на размер), принимается равным 6σ, т.е. TA_i = 6σ.

Если суммарная погрешность средства измерения 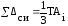, то выход размеров A_i за пределы ±3σ не превышает 0,27%. В пределах ±3σ, годных A_i – 99,73%. Выход размеров деталей (A_i) за границы поля допуска T(A_i) возможен только в случаях II, когда на измерения поступают детали с действительными размерами (A_i)_Д < (A_i)_MIN, либо в случае IV, когда на измерения поступают детали с действительными размерами (A_i)_Д > (A_i)_MAX.

В остальных случаях (например, случай III) суммарная погрешность измерения 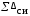обеспечивает измерения X_i размеров детали A_i, невыходящими за пределы поля допуска T(A_i).

Верхнее ES(A_Δ) и нижнее EI(A_Δ) отклонения замыкающего звена при расчётах вероятностным методом определяют по формулам:

,

.

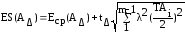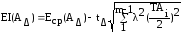3