
Социальо-экономическое прогнозирование_Хвощин
.pdf
КВ МВЪ, ЪУ ФрЛ‰ВЪТfl УЪ‚Вр„МЫЪ¸ ФрВ‰ФУОУКВМЛВ, ‚˚‰‚ЛМЫЪУВ УЪМУТЛЪВО¸МУ ‚ВОЛ˜ЛМ˚ α Ë β:
b − Sb ×têðèò<β < b + Sb ×têðèò,
a − Sa ×têðèò< α < а + Sb ×têðèò.
д‡Н Л ‚ ТОЫ˜‡В Ф‡рМУИ ОЛМВИМУИ рВ„рВТТЛЛ, ‰Оfl ‡М‡ОЛБ‡ ТЪ‡ЪЛТЪЛ˜ВТНУИ БМ‡˜ЛПУТЪЛ ФУОЫ˜ВММ˚ı УˆВМУН НУ˝ЩЩЛˆЛВМЪУ‚ ПМУКВТЪ‚ВММУИ ОЛМВИМУИ рВ„рВТТЛЛ МВУ·ıУ‰ЛПУ УˆВМЛЪ¸ ‰ЛТФВрТЛ˛ Л ТЪ‡М‰‡рЪМ˚В УЪНОУМВМЛfl НУ˝ЩЩЛˆЛВМЪУ‚ aj.
Ç Ó·˘ÂÏ ÒÎÛ˜‡Â ‰ËÒÔÂрÒËfl ÍÓ˝ÙÙˈËÂÌÚ‡ aj Varaj ÓÔр‰ÂÎflÂÚÒfl ÔÓ ÙÓрÏÛÎÂ:
Var |
= S 2 |
= |
∑Xi2 ×Z jj |
, |
|
||||
a j |
a j |
|
n − m −1 |
|
|
|
|
||
„‰Â Sa — ТЪ‡М‰‡рЪМУВ УЪНОУМВМЛВ ‚ВОЛ˜ЛМ aj; Zjj — ‰Л‡„УМ‡О¸М˚В ˝ОВПВМЪj ˚ χÚрˈ˚ (XTX)–1; m — ˜ЛТОУ МВБ‡‚ЛТЛП˚ı ФВрВПВММ˚ı ‚ ПУ‰ВОЛ. йЪТ˛‰‡ ‰Оfl ФрУ‚ВрНЛ „ЛФУЪВБ˚ У ‚ВОЛ˜ЛМВ Н‡К‰У„У ЛБ НУ- ˝ЩЩЛˆЛВМЪУ‚ р‡ТТ˜ЛЪ˚‚‡˛ЪТfl, Н‡Н Л ‚ ТОЫ˜‡В Ф‡рМУИ ОЛМВИМУИ рВ„рВТТЛЛ, t-ТЪ‡ЪЛТЪЛНЛ НУ˝ЩЩЛˆЛВМЪУ‚:
t = |
a j |
= |
a j |
, |
|
Var |
Sb |
||||
|
|
|
|||
|
b |
|
|
|
ı‡р‡НЪВрЛБЫ˛˘ЛВТfl р‡ТФрВ‰ВОВМЛВП лЪ¸˛‰ВМЪ‡ Т n–m–1 ТЪВФВМflПЛ Т‚У·У‰˚.
СУ‚ВрЛЪВО¸М˚В ЛМЪВр‚‡О˚ УФрВ‰ВОfl˛ЪТfl ‡М‡ОУ„Л˜МУ ТОЫ˜‡˛ Т Ф‡рМУИ рВ„рВТТЛВИ.
СОfl УˆВМНЛ ТЪВФВМЛ ТУУЪ‚ВЪТЪ‚Лfl ОЛМЛЛ рВ„рВТТЛЛ ‚˚·УрУ˜М˚П
‰‡ÌÌ˚Ï Ó·˚˜ÌÓ ÔрËÏÂÌflÂÚÒfl НУ˝ЩЩЛˆЛВМЪ ‰ВЪВрПЛМ‡ˆЛЛ R2:
R |
2 |
|
ÑÊÐ |
∑(Yi′−Yñð)2 |
|
|
||||||
|
= |
|
|
|
= |
∑(Yi −Yñð)2 |
, |
|
||||
|
|
|
|
|
||||||||
|
|
|
ÎÑÊ |
|
|
|||||||
ËÎË |
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
ÑÊÎ |
′ |
2 |
|
||||
R2 =1 |
|
|
(Yi −Yi ) |
|
||||||||
− |
|
|
|
= |
|
|
. |
|||||
|
|
|
∑(Yi −Yñð)2 |
|||||||||
|
|
|
|
|
ÎÑÊ |
|
||||||
|
|
|
|
|
141 |
|
|
|
||||

й·˘‡fl ТЫПП‡ Н‚‡‰р‡ЪУ‚ УЪНОУМВМЛИ (йлд) — ˝ЪУ ТЫПП‡ Н‚‡‰- р‡ЪУ‚ р‡БМУТЪВИ ПВК‰Ы ‚˚·УрУ˜М˚ПЛ (М‡·О˛‰‡ВП˚ПЛ) БМ‡˜ВМЛflПЛ Б‡‚ЛТЛПУИ ФВрВПВММУИ Yi Ë Òр‰ÌÂÈ ËÁ ̇·Î˛‰ÂÌËÈ ‚ ‚˚·ÓрÍ YÒр.
лЫПП‡ Н‚‡‰р‡ЪУ‚ УЪНОУМВМЛИ, У·˙flТМЛП‡fl рВ„рВТТЛВИ (лдк), — ˝ЪУ ТЫПП‡ Н‚‡‰р‡ЪУ‚ р‡БМУТЪВИ ПВК‰Ы ФрУ„МУБЛрЫВП˚ПЛ М‡ УТМУ‚В М‡И‰ВММУ„У Ыр‡‚МВМЛfl рВ„рВТТЛЛ БМ‡˜ВМЛflПЛ Yi′ Ë Òр‰ÌÂÈ ËÁ ̇·Î˛- ‰ÂÌËÈ ‚ ‚˚·ÓрÍ YÒр.
йТЪ‡ЪУ˜М‡fl ТЫПП‡ Н‚‡‰р‡ЪУ‚ (лдй) — ˝ЪУ ТЫПП‡ Н‚‡‰р‡ЪУ‚ р‡БМУТЪВИ ПВК‰Ы ‚˚·УрУ˜М˚ПЛ (М‡·О˛‰‡ВП˚ПЛ) БМ‡˜ВМЛflПЛ Yi Л р‡ТТ˜ЛЪ‡ММ˚ПЛ М‡ УТМУ‚В М‡И‰ВММУ„У Ыр‡‚МВМЛfl рВ„рВТТЛЛ Yi′.
äÓ˝ÙÙˈËÂÌÚ ‰ÂÚÂрÏË̇ˆËË ÔрËÌËχÂÚ Á̇˜ÂÌËfl ÓÚ 0, ÍÓ„‰‡ Ù‡ÍÚÓр˚ X МВ УН‡Б˚‚‡˛Ъ МЛН‡НУ„У ‚ОЛflМЛfl М‡ Б‡‚ЛТЛПЫ˛ ФВрВПВММЫ˛, ‰У 1, НУ„‰‡ ЛБПВМВМЛfl Б‡‚ЛТЛПУИ ФВрВПВММУИ Y ФУОМУТЪ¸˛ У·˙flТМЛП˚ ‚ОЛflМЛВП Щ‡НЪУрУ‚ ПУ‰ВОЛ.
й‰М‡НУ ‚ ПМУ„УЩ‡НЪУрМУИ рВ„рВТТЛЛ НУ˝ЩЩЛˆЛВМЪ ‰ВЪВрПЛМ‡- ˆЛЛ НУррВНЪЛрЫ˛Ъ Т Ы˜ВЪУП ˜ЛТО‡ МВБ‡‚ЛТЛП˚ı ФВрВПВММ˚ı, р‡Т- Т˜ЛЪ˚‚‡˛Ъ ТНУррВНЪЛрУ‚‡ММ˚И R2 − R2′ :
R2′ =1−(1− R2 )− nn−−m1 ,
„‰Â n — ˜ËÒÎÓ Ì‡·Î˛‰ÂÌËÈ; m — ˜ЛТОУ МВБ‡‚ЛТЛП˚ı ФВрВПВММ˚ı. дУ˝ЩЩЛˆЛВМЪ ‰ВЪВрПЛМ‡ˆЛЛ fl‚ОflВЪТfl R2 ТОЫ˜‡ИМУИ ‚ВОЛ˜ЛМУИ, ФУТНУО¸НЫ Y — ТОЫ˜‡ИМ‡fl ФВрВПВММ‡fl. дрЛЪВрЛИ ФрУ‚ВрНЛ БМ‡˜Л- ПУТЪЛ R2 ЛПВВЪ F-р‡ТФрВ‰ВОВМЛВ. щЪУ р‡ТФрВ‰ВОВМЛВ У·О‡‰‡ВЪ ‰‚Ы- Пfl ТЪВФВМflПЛ Т‚У·У‰˚: У‰МУ БМ‡˜ВМЛВ ‚ ˜ЛТОЛЪВОВ НрЛЪВрЛfl ФрУ- ‚ВрНЛ (У·УБМ‡˜‡ВЪТfl v1), ‚ÚÓрÓ — ‚ Á̇ÏÂ̇ÚÂΠ(v2). Ç ÍрËÚÂрËË ÔрÓ‚ÂрÍË ‰Îfl R2 ˜ЛТОЛЪВО˛ ТУУЪ‚ВЪТЪ‚ЫВЪ ТЪВФВМ¸ Т‚У·У‰˚ 1 Ë Á̇- ÏÂ̇ÚÂβ — n – 2 ТЪВФВМВИ Т‚У·У‰˚. л‡П НрЛЪВрЛИ ФрУ‚ВрНЛ ‰Оfl
R2 р‡ÒÒ˜ËÚ˚‚‡ÂÚÒfl Ú‡Í:
F = R |
2 |
÷ |
1− R2 |
. |
|
|||
|
n −2 |
|
||||||
|
|
|
|
|
|
|
||
ÑÎfl ÒÍÓррÂÍÚËрÓ‚‡ÌÌÓ„Ó R2 ÍрËÚÂрËÈ ÔрÓ‚ÂрÍË ‚˚˜ËÒÎflÂÚÒfl |
||||||||
Ú‡Í: |
|
|
|
|
|
|
|
|
F = |
|
R2 |
× |
n −k |
, |
|||
|
− R2 |
k − |
1 |
|||||
1 |
|
|
||||||
|
|
|
142 |
|
|
|
||

„‰Â n — ˜ËÒÎÓ Ì‡·Î˛‰ÂÌËÈ; k — ˜ЛТОУ МВБ‡‚ЛТЛП˚ı ФВрВПВММ˚ı ‚ Ыр‡‚МВМЛЛ рВ„рВТТЛЛ. щЪУЪ НрЛЪВрЛИ ФрУ‚ВрНЛ ЛПВВЪ F–р‡Т- ФрВ‰ВОВМЛВ ТУ ТЪВФВМflПЛ Т‚У·У‰˚ v1 = k – 1 Ë v2 = n – k.
н‡НКВ ‰Оfl ПМУКВТЪ‚ВММУИ рВ„рВТТЛЛ ЛПВВЪ ТП˚ТО р‡ТТ˜ЛЪ‡Ъ¸ ˜‡ТЪМ˚В НУ˝ЩЩЛˆЛВМЪ˚ ‰ВЪВрПЛМ‡ˆЛЛ dx1 Ë d x2 . çÓ ÔÂр‰ ˝ÚËÏ Úр·ÛÂÚÒfl ÓÔр‰ÂÎËÚ¸ Ô‡рÌ˚ ÍÓ˝ÙÙˈËÂÌÚ˚ ÍÓррÂÎflˆËË ÏÂʉÛ
ФВрВПВММ˚ПЛ ПУ‰ВОЛ: ryx1 , ryx2 , rx1x2 Л Ъ. ‰. аı р‡ТТ˜ЛЪ˚‚‡˛Ъ ‰Оfl УФрВ‰ВОВМЛfl ЪВТМУЪ˚ Т‚flБЛ ПВК‰Ы ФВрВПВММ˚ПЛ ПУ‰ВОЛ, М‡ УТМУ‚В
БМ‡˜ВМЛfl Ф‡рМ˚ı НУ˝ЩЩЛˆЛВМЪУ‚ НУррВОflˆЛЛ ПУКМУ ФрЛМflЪ¸ рВ- ¯ВМЛВ У ‚НО˛˜ВМЛЛ ЛОЛ МВ‚НО˛˜ВМЛЛ Щ‡НЪУрМУИ ФВрВПВММУИ ‚ ЛЪУ„У‚Ы˛ рВ‰‡НˆЛ˛ ПУ‰ВОЛ. и‡рМ˚В ОЛМВИМ˚В НУ˝ЩЩЛˆЛВМЪ˚ НУррВОflˆЛЛ УФрВ‰ВОfl˛ЪТfl М‡ УТМУ‚В ЩУрПЫО˚:
r= (xy)ср − xср yср ,
σx ×σy
„‰Â σı Ë σÛ — ТрВ‰МВН‚‡‰р‡ЪЛ˜ВТНЛВ УЪНОУМВМЛfl ‚˚·УрУ˜М˚ı БМ‡- ˜ВМЛИ ФУН‡Б‡ЪВОВИ ı Ë Û, ‰Оfl НУЪУр˚ı р‡ТТ˜ЛЪ˚‚‡ВЪТfl НУ˝ЩЩЛˆЛВМЪ НУррВОflˆЛЛ, УЪ ‚˚·УрУ˜МУИ ТрВ‰МВИ. ЗВОЛ˜ЛМ‡ ТрВ‰МВН‚‡‰р‡ЪЛ˜В- ТНУ„У УЪНОУМВМЛfl ‚˚·УрУ˜МУ„У БМ‡˜ВМЛfl Н‡НУ„У-ОЛ·У ФУН‡Б‡ЪВОfl (М‡ФрЛПВр, ı), Н‡Н ‚˚ ФУПМЛЪВ ЛБ НЫрТ‡ ТЪ‡ЪЛТЪЛНЛ, р‡‚М‡ Н‚‡‰р‡Ъ- МУПЫ НУрМ˛ ЛБ В„У ‰ЛТФВрТЛЛ:
2 |
= |
∑(x − xср)2 |
. |
σx = σx |
n |
||
|
|
|
дУ˝ЩЩЛˆЛВМЪ ПМУКВТЪ‚ВММУИ НУррВОflˆЛЛ ‰Оfl УˆВМНЛ Б‡‚ЛТЛПУТЪЛ рВБЫО¸ЪЛрЫ˛˘ВИ ФВрВПВММУИ УЪ Щ‡НЪУрМ˚ı ‚ Ф‡рМУИ рВ„рВТТЛЛ р‡ТТ˜ЛЪ˚‚‡ВЪТfl ФУ ТОВ‰Ы˛˘ВИ ЩУрПЫОВ:
Ryx x |
= |
ryx1 + ryx2 − 2ryx1 ryx2 ryx1 x2 . |
|
1 |
2 |
1 − rx x |
|
|
|
||
|
|
1 |
2 |
щЪУЪ НУ˝ЩЩЛˆЛВМЪ НУОВ·ОВЪТfl ‚ ФрВ‰ВО‡ı УЪ 0 ‰У 1 (НУОВ·‡МЛfl БМ‡˜ВМЛИ ФВрВПВММУИ Y ‡·ТУО˛ЪМУ МВ Б‡‚ЛТflЪ ЛОЛ ФУОМУТЪ¸˛ Б‡‚Л- ТflЪ УЪ ЛБПВМВМЛfl БМ‡˜ВМЛИ Щ‡НЪУрУ‚ X), ˜ВП В„У БМ‡˜ВМЛВ ·ОЛКВ Н 1, ЪВП ФУОМВВ Ы˜ЪВМ˚ ‚ТВ Щ‡НЪУр˚, ‚ОЛfl˛˘ЛВ М‡ Y.
143

З У·˘ВП ТОЫ˜‡В ЩУрПЫО‡ НУ˝ЩЩЛˆЛВМЪ‡ ПМУКВТЪ‚ВММУИ НУррВОflˆЛЛ ‚˚„Оfl‰ЛЪ Ъ‡Н:
R =  1− ОСКСКО.
1− ОСКСКО.
у‡ТЪМ˚В НУ˝ЩЩЛˆЛВМЪ˚ ‰ВЪВрПЛМ‡ˆЛЛ ‚ ПМУ„УЩ‡НЪУрМ˚ı ПУ- ‰ВОflı ТОЫК‡Ъ ‰Оfl ‡М‡ОЛБ‡ ЪВТМУЪ˚ Т‚flБЛ ПВК‰Ы рВБЫО¸Ъ‡ЪЛ‚МУИ Л У‰МУИ ЛБ Щ‡НЪУрМ˚ı ФВрВПВММ˚ı ФрЛ МВЛБПВММУП БМ‡˜ВМЛЛ УТ- Ъ‡О¸М˚ı Щ‡НЪУрУ‚. йМЛ ФУН‡Б˚‚‡˛Ъ, М‡ ТНУО¸НУ ‚ ФрУˆВМЪМУП ТУУЪМУ¯ВМЛЛ ЛБПВМЛЪТfl БМ‡˜ВМЛВ Б‡‚ЛТЛПУИ ФВрВПВММУИ ФрЛ ЛБПВМВМЛЛ ‰‡ММУ„У Щ‡НЪУр‡ Л МВЛБПВММ˚ı ФрУ˜Лı:
dx j = ryx j ×a j × |
σx |
j |
, |
|
|
||
|
σy |
||
„‰Â ryxj — Ф‡рМ˚И НУ˝ЩЩЛˆЛВМЪ НУррВОflˆЛЛ Щ‡НЪУрМУИ ФВрВПВММУИ j Л Б‡‚ЛТЛПУИ ФВрВПВММУИ Y; aj — ÓˆÂÌ͇ ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘Â„Ó ÍÓ˝Ù-
ЩЛˆЛВМЪ‡ рВ„рВТТЛЛ ФрЛ ‰‡ММУП Щ‡НЪУрВ ‚ Ыр‡‚МВМЛЛ рВ„рВТТЛЛ; σx j Ë σÛ — ТрВ‰МВН‚‡‰р‡ЪЛ˜ВТНЛВ УЪНОУМВМЛfl БМ‡˜ВМЛИ р‡ТТП‡ЪрЛ- ‚‡ВПУ„У Щ‡НЪУр‡ Л Y.
у‡ТЪМ˚В НУ˝ЩЩЛˆЛВМЪ˚ НУррВОflˆЛЛ ЛТФУО¸БЫ˛ЪТfl ‰Оfl ЛБПВрВМЛfl ЪВТМУЪ˚ Т‚flБЛ ПВК‰Ы ‰‡ММ˚П Щ‡НЪУрУП Л Б‡‚ЛТЛПУИ ФВрВПВММУИ ПУ‰ВОЛ ФрЛ МВЛБПВММ˚ı ФрУ˜Лı Щ‡НЪУр‡ı:
—ryx1x2 — ФрЛ У‰МУП МВЛБПВММУП Щ‡НЪУрВ x2 — НУ˝ЩЩЛˆЛВМЪ ˜‡ТЪМУИ НУррВОflˆЛЛ ФВр‚У„У ФУрfl‰Н‡;
—ryx1x2 x3 — ФрЛ ‰‚Ыı МВЛБПВММ˚ı Щ‡НЪУр‡ı x2 Ë x3 — НУ˝ЩЩЛˆЛВМЪ ˜‡ТЪМУИ НУррВОflˆЛЛ ‚ЪУрУ„У ФУрfl‰Н‡;
—ryx1x2 ...xm — ФрЛ МВЛБПВММУП ‰ВИТЪ‚ЛЛ ‚ТВı Щ‡НЪУрУ‚, ‚НО˛- ˜ВММ˚ı ‚ Ыр‡‚МВМЛВ рВ„рВТТЛЛ — НУ˝ЩЩЛˆЛВМЪ ˜‡ТЪМУИ НУррВОfl-
ˆËË (m – 1)-„Ó ÔÓрfl‰Í‡.
äÓ˝ÙÙˈËÂÌÚ˚ Ô‡рÌÓÈ ÍÓррÂÎflˆËË Ì‡Á˚‚‡˛Ú ÍÓ˝ÙÙˈËÂÌÚ‡ÏË ÌÛÎÂ‚Ó„Ó ÔÓрfl‰Í‡.
у‡ТЪМ˚В НУ˝ЩЩЛˆЛВМЪ˚ НУррВОflˆЛЛ ПУКМУ р‡ТТ˜ЛЪ‡Ъ¸ ‚ ТУУЪ- ‚ВЪТЪ‚ЛЛ ТУ ТОВ‰Ы˛˘ВИ ЩУрПЫОУИ:
r |
|
|
= |
1− |
1 |
− Ryx2 |
x |
|
|
...x |
...x |
|
, |
|||||
|
|
|
− Ryx2 |
1 |
|
2 |
|
|
i |
|
|
m |
||||||
yx1 |
x1 x2 |
...xi−1 xi+1 ...xm |
|
|
1 |
...x |
i−1 |
x |
i+1 |
...x |
m |
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
144
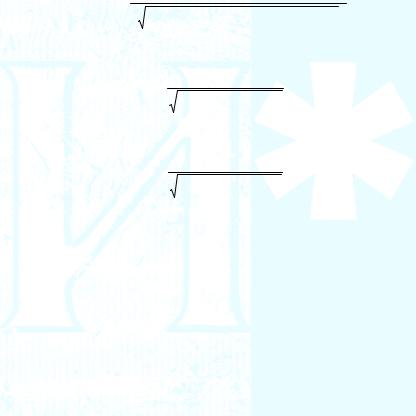
„‰Â Ryx2 |
x |
...x ...x |
— ПМУКВТЪ‚ВММ˚И НУ˝ЩЩЛˆЛВМЪ ‰ВЪВрПЛМ‡ˆЛЛ ‚ТВ„У |
|||||||
1 |
2 |
i m |
m Ù‡ÍÚÓрÓ‚ Ò Y; Ryx2 |
|
|
|
|
|
|
|
НУПФОВНТ‡ ЛБ |
x |
...x |
i −1 |
x |
i +1 |
...x |
— ÔÓ͇Á‡ÚÂθ ‰ÂÚÂр- |
|||
|
|
|
1 |
2 |
|
|
|
m |
||
ÏË̇ˆËË, ÌÓ ‰Îfl ÏÓ‰ÂÎË, Ì ‚Íβ˜‡˛˘ÂÈ Ù‡ÍÚÓр xi.
иУПЛПУ ˝ЪУ„У, НУ˝ЩЩЛˆЛВМЪ˚ ˜‡ТЪМУИ НУррВОflˆЛЛ ·УОВВ ‚˚ТУНЛı ФУрfl‰НУ‚ ПУКМУ УФрВ‰ВОЛЪ¸ ˜ВрВБ НУ˝ЩЩЛˆЛВМЪ˚ ·УОВВ МЛБНЛı ФУрfl‰НУ‚ ФУ ЩУрПЫОВ:
ryx x x |
|
|
= |
ryx x x |
|
...x |
|
|
−ryx |
|
x x |
|
...x |
|
×rx x |
|
x x |
|
...x |
m−1 . |
|||||||
2 |
...x |
1 1 |
2 |
|
m−1 |
|
|
m |
1 |
2 |
|
m−1 |
|
|
i |
m |
|
|
1 |
2 |
|
||||||
1 1 |
|
m |
(1−r 2 |
|
|
|
|
|
|
) ×(1−r 2 |
|
|
|
|
|
|
|
|
|
) |
|||||||
|
|
|
|
|
|
x x |
|
...x |
|
x |
|
x x |
|
...x |
|
||||||||||||
|
|
|
|
|
|
yx |
m |
2 |
m−1 |
|
|
|
x |
m |
2 |
m−1 |
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
i |
|
1 |
|
|
|
|
||||||||
èрË ‰‚Ûı Ù‡ÍÚÓр‡ı Ë i = 1 ‰‡Ì̇fl ÙÓрÏÛ· ÔрËÏÂÚ ‚ˉ:
ryx |
|
|
= |
ryx |
−ryx |
2 |
×rx x |
2 |
. |
|||
x |
|
|
1 |
|
|
1 |
|
|||||
2 |
|
|
|
|
|
|
|
|
||||
1 |
|
|
(1 |
−r 2 |
) × |
(1−r 2 |
) |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
yx |
2 |
|
|
x x |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
||
èрË ‰‚Ûı Ù‡ÍÚÓр‡ı Ë i = 2 ‰‡Ì̇fl ÙÓрÏÛ· ·Û‰ÂÚ ‚˚„Îfl‰ÂÚ¸:
ryx |
|
= |
ryx |
2 |
−ryx |
×rx x |
2 |
. |
||||
x |
|
|
|
1 |
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
||||
2 |
1 |
(1 |
−r 2 |
) × |
(1 |
−r 2 |
) |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
yx |
|
|
|
x x |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
иУПЛПУ ˝ЪЛı ФУН‡Б‡ЪВОВИ, ‚ОЛflМЛВ УЪ‰ВО¸М˚ı Щ‡НЪУрУ‚ М‡ рВ-
БЫО¸ЪЛрЫ˛˘Ы˛ ФВрВПВММЫ˛ ‚ ПМУ„УЩ‡НЪУрМ˚ı ПУ‰ВОflı ПУКВЪ ·˚Ъ¸ Уı‡р‡НЪВрЛБУ‚‡МУ Т ФУПУ˘¸˛ ˜‡ТЪМ˚ı НУ˝ЩЩЛˆЛВМЪУ‚ ˝О‡ТЪЛ˜МУТЪЛ, ÓÔр‰ÂÎflÂÏ˚ı ÔÓ ÙÓрÏÛÎÂ:
эx j = a j × |
x jср |
, |
|
yср |
|||
|
|
„‰Â xjср — ТрВ‰МВВ БМ‡˜ВМЛВ ТУУЪ‚ВЪТЪ‚Ы˛˘ВИ Щ‡НЪУрМУИ ФВрВПВММУИ; ÛÒр — ТрВ‰МВВ БМ‡˜ВМЛВ рВБЫО¸ЪЛрЫ˛˘ВИ ФВрВПВММУИ; aj — НУ˝ЩЩЛˆЛВМЪ ФрЛ ‰‡ММУП Щ‡НЪУрВ ‚ Ыр‡‚МВМЛЛ рВ„рВТТЛЛ. йМЛ ФУН‡Б˚‚‡˛Ъ, М‡ ТНУО¸НУ ФрУˆВМЪУ‚ ЛБПВМЛЪТfl ‚ВОЛ˜ЛМ‡ рВБЫО¸ЪЛрЫ˛˘ВИ ФВрВПВММУИ ФрЛ ЛБПВМВМЛЛ ‰‡ММУ„У Щ‡НЪУр‡ М‡ 1% Л МВЛБПВММ˚ı ФрУ˜Лı.
нВТЪЛрУ‚‡МЛВ ‚˚ФУОМВМЛfl ‰УФЫ˘ВМЛИ ПВЪУ‰‡ М‡ЛПВМ¸¯Лı Н‚‡‰р‡ЪУ‚ ‚ ПУ‰ВОЛ ОЛМВИМУИ рВ„рВТТЛЛ
уЪУ·˚ УТЫ˘ВТЪ‚ЛЪ¸ ФрУ‚ВрНЫ ПУ‰ВОЛ М‡ ‚˚ФУОМВМЛВ ‰УФЫ˘ВМЛИ ПВЪУ‰‡ М‡ЛПВМ¸¯Лı Н‚‡‰р‡ЪУ‚, МВУ·ıУ‰ЛПУ ФрУ‚ВрЛЪ¸ ПУ‰ВО¸ М‡:
145

— „ВЪВрУТНВ‰‡ТЪЛ˜МУТЪ¸: fl‚ОflВЪТfl ОЛ р‡ТФрВ‰ВОВМЛВ УТЪ‡Ъ-
НУ‚, У¯Л·УН рВ„рВТТЛЛ ФУТЪУflММ˚П („УПУТНВ‰‡ТЪЛ˜М˚П), ЛОЛ КВ МВЪ;
— ‡‚ЪУНУррВОflˆЛ˛: fl‚Îfl˛ÚÒfl ÎË Á̇˜ÂÌËfl ÓÒÚ‡ÚÍÓ‚, ӯ˷ÓÍ
МВБ‡‚ЛТЛП˚ПЛ, ЛОЛ ЛПВВЪ ПВТЪУ fl‚ОВМЛВ ‡‚ЪУНУррВОflˆЛЛ УТЪ‡ЪНУ‚;
— ПЫО¸ЪЛНУООЛМВ‡рМУТЪ¸: fl‚Оfl˛ЪТfl ОЛ МВБ‡‚ЛТЛП˚В ФВрВПВММ˚В МВНУррВОЛрУ‚‡ММ˚ПЛ.
лЫ˘ВТЪ‚ЫВЪ ·УО¸¯УВ ˜ЛТОУ ЪВТЪУ‚ ‰Оfl ФрУ‚ВрНЛ М‡ „ВЪВрУТНВ‰‡- ТЪЛ˜МУТЪ¸: ЪВТЪ р‡М„У‚УИ НУррВОflˆЛЛ лФЛрПВМ‡, ЪВТЪ ЙОВИБВр‡, ЪВТЪ ЙУО‰ЩВО‰‡-䂇̉ڇ, ЕрВЫ¯‡-臄‡М‡31 Л ‰р. й‰МЛП ЛБ М‡Л·УОВВ ФУФЫОflрМ˚ı ЪВТЪУ‚ fl‚ОflВЪТfl ЪВТЪ ЙУО‰ЩВО‰‡-䂇̉ڇ. д‡Н Фр‡‚ЛОУ, В„У ФрЛПВМfl˛Ъ, ВТОЛ ВТЪ¸ ФрВ‰ФУОУКВМЛВ У ФрflПУИ Б‡‚ЛТЛПУТЪЛ ‰ЛТФВрТЛЛ У¯Л·НЛ УЪ ‚ВОЛ˜ЛМ˚ МВНУЪУрУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ ПУ‰В- ОЛ. СОfl ˝ЪУ„У М‡‰У ‰ВИТЪ‚У‚‡Ъ¸ ФУ ТОВ‰Ы˛˘ВПЫ ‡О„УрЛЪПЫ:
1)‚ТВ М‡·О˛‰ВМЛfl ЫФУрfl‰У˜Л‚‡˛ЪТfl ФУ ‚ВОЛ˜ЛМВ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ, УЪМУТЛЪВО¸МУ НУЪУрУИ ВТЪ¸ ФУ‰УБрВМЛВ М‡ „ВЪВрУТНВ‰‡- ТЪЛ˜МУТЪ¸;
2)УТЪ‡ЪНЛ ‚ ˝ЪУИ ЫФУрfl‰У˜ВММУИ ТУ‚УНЫФМУТЪЛ ‰ВОflЪ М‡ ‰‚В р‡‚М˚В „рЫФФ˚, ФрЛ ˜ВП М‡ıУ‰fl˘ЛВТfl ФУТрВ‰ЛМВ ПВК‰Ы МЛПЛ d М‡- ·О˛‰ВМЛИ ЛТНО˛˜‡˛ЪТfl ЛБ р‡ТТПУЪрВМЛfl (d У·˚˜МУ р‡‚МУ УНУОУ ¼ ÓÚ Ó·˘Â„Ó ÍÓ΢ÂÒÚ‚‡ ̇·Î˛‰ÂÌËÈ);
3)р‡ТТ˜ЛЪ˚‚‡˛ЪТfl ‰‚В МВБ‡‚ЛТЛП˚В рВ„рВТТЛЛ ФУ ФВр‚УИ Л ‚ЪУрУИ „рЫФФВ, НУОЛ˜ВТЪ‚У М‡·О˛‰ВМЛИ ‚ НУЪУр˚ı ТУТЪ‡‚ОflВЪ n/2 – d/2 (ФрЛ ˝ЪУП ‰УОКМУ ·˚Ъ¸ n/2 – d/2 > k + 1, „‰Â k — ˜ЛТОУ МВБ‡‚ЛТЛ- П˚ı ФВрВПВММ˚ı), Л М‡ıУ‰flЪТfl ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ УТЪ‡ЪНЛ ‰Оfl ФВр‚УИ
ˉОfl ‚ЪУрУИ рВ„рВТТЛЛ Â1 Ë Â2;
4)ВТОЛ ФрВ‰ФУОУКВМЛВ У ФрflПУИ Б‡‚ЛТЛПУТЪЛ ‰ЛТФВрТЛЛ У¯Л·- НЛ УЪ ‚ВОЛ˜ЛМ˚ ‰‡ММУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ ‚ВрМУ, ЪУ ‚ ФВр‚УИ
„рÛÔÔ ÒÛÏχ Í‚‡‰р‡ÚÓ‚ ÓÒÚ‡ÚÍÓ‚ (‡ Á̇˜ËÚ, Ë Ëı ‰ËÒÔÂрÒËfl) ·Û‰ÂÚ ÏÂ̸¯Â, ˜ÂÏ ‚Ó ‚ÚÓрÓÈ; Á‡ÚÂÏ р‡ÒÒ˜ËÚ˚‚‡˛Ú НрЛЪВрЛИ ЙУО‰ЩВО- ‰‡-䂇̉ڇ: ‚ ТОЫ˜‡В ФрВ‰ФУОУКВМЛfl ФрflПУИ ФрУФУрˆЛУМ‡О¸МУ-
ТЪЛ ПВК‰Ы ‚ВОЛ˜ЛМУИ ‰ЛТФВрТЛЛ УЪНОУМВМЛИ Л БМ‡˜ВМЛВП МВБ‡‚Л-
31 лП., М‡ФрЛПВр: СУЫ„ВрЪЛ д. З‚В‰ВМЛВ ‚ ˝НУМУПВЪрЛНЫ: иВр. Т ‡М„О. е.: азокД-е, 1999. л. 206–208; нВррЛ СК. мУр¯ВП, дВИЪ и‡рр‡ПУЫ. дУОЛ˜ВТЪ‚ВММ˚В ПВЪУ‰˚ ‚ ЩЛМ‡МТ‡ı: м˜В·. ФУТУ·ЛВ ‰Оfl ‚ЫБУ‚: иВр. Т ‡М„О. / иУ‰ рВ‰. е. к. ЦЩЛПУ- ‚УИ. е.: оЛМ‡МТ˚: ызана, 1999. л. 286–287; 凄МЫТ ь. к., д‡Ъ˚¯В‚ и. д., иВрВТВˆНЛИ Д. Д. щНУМУПВЪрЛН‡. з‡˜‡О¸М˚И НЫрТ: м˜В·. ФУТУ·ЛВ. 2-В ЛБ‰., ЛТФр. е.: СВОУ, 1998. л. 112–113; щНУМУПВЪрЛН‡: м˜В·. / иУ‰ рВ‰. а. а. ЦОЛТВВ‚УИ. е.: оЛМ‡МТ˚ Л ТЪ‡ЪЛТЪЛН‡, 2001. л. 155–169.
146

ТЛПУИ ФВрВПВММУИ ТЫППЫ Н‚‡‰р‡ЪУ‚ УТЪ‡ЪНУ‚ ‚У ‚ЪУрУИ „рЫФФВ ‰В- ОflЪ М‡ ТЫППЫ Н‚‡‰р‡ЪУ‚ УТЪ‡ЪНУ‚ ‚ ÔÂð‚ÓÈ. к‡ТТ˜ЛЪ‡ММ˚И НрЛЪВрЛИ ЛПВВЪ F-р‡ТФрВ‰ВОВМЛВ Т n/2 – d/2–k Ë n/2 – d/2 – k ТЪВФВМflПЛ Т‚У·У‰˚. З ТОЫ˜‡В У·р‡ЪМУИ ФрУФУрˆЛУМ‡О¸МУТЪЛ ‰ЛТФВрТЛЛ УЪНОУМВМЛИ БМ‡˜ВМЛ˛ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ ТЫППЫ Н‚‡‰р‡ЪУ‚ УТЪ‡ЪНУ‚ ‚ ÔÂð‚ÓÈ „рЫФФВ ‰ВОflЪ М‡ ТЫППЫ Н‚‡‰р‡ЪУ‚ УТЪ‡ЪНУ‚ ‚У ‚ЪУрУИ, р‡Т- ФрВ‰ВОВМЛВ НрЛЪВрЛfl Ъ‡НКВ ЛПВВЪ ‚Л‰ F-р‡ТФрВ‰ВОВМЛfl Т ЪВПЛ КВ ТЪВФВМflПЛ Т‚У·У‰˚.
З ТОЫ˜‡В М‡ОЛ˜Лfl „ВЪВрУТНВ‰‡ТЪЛ˜МУТЪЛ УТЪ‡ЪНУ‚ ‰Оfl УФрВ‰В- ОВМЛfl Ф‡р‡ПВЪрУ‚ рВ„рВТТЛЛ ФрЛПВМflВЪТfl Ó·Ó·˘ÂÌÌ˚È ÏÂÚÓ‰ ̇ËÏÂ̸¯Ëı Í‚‡‰ð‡ÚÓ‚ (Generalized Least Squares, GLS). éÌ
ФрЛПВМflВЪТfl Н ФрВУ·р‡БУ‚‡ММ˚П ‰‡ММ˚П Л ФУБ‚УОflВЪ ФУОЫ˜‡Ъ¸ УˆВМНЛ, НУЪУр˚В МВ ЪУО¸НУ У·О‡‰‡˛Ъ Т‚УИТЪ‚УП МВТПВ˘ВММУТЪЛ, МУ ЛПВ˛Ъ М‡ЛПВМ¸¯ЛВ ‚˚·УрУ˜М˚В ‰ЛТФВрТЛЛ.
Д‚ЪУНУррВОflˆЛfl (ТВрЛ‡О¸М‡fl НУррВОflˆЛfl) — fl‚ОВМЛВ Б‡‚ЛТЛПУТЪЛ ‚ВОЛ˜ЛМ˚ УТЪ‡ЪНУ‚ ‰рЫ„ УЪ ‰рЫ„‡, ФУТНУО¸НЫ ЪВНЫ˘ЛВ БМ‡˜В- МЛfl Y М‡ıУ‰flЪТfl ФУ‰ ‚ОЛflМЛВП ‚ВОЛ˜ЛМ˚ ФрУ¯О˚ı БМ‡˜ВМЛИ. Д‚ЪУНУррВОflˆЛfl ПУКВЪ ФУfl‚ЛЪ¸Тfl ЛБ-Б‡ МВ‰УЫ˜ВЪ‡ (УФЫ˘ВМЛfl) ФВрВПВМ- М˚ı, МВ‚ВрМУИ ЩУрП˚ ЩЫМНˆЛЛ, УˆВМЛ‚‡˛˘ВИ Б‡‚ЛТЛПУТЪ¸ рВБЫО¸- ЪЛрЫ˛˘ВИ ФВрВПВММУИ УЪ Щ‡НЪУрМ˚ı (М‡ФрЛПВр, ОЛМВИМ‡fl ПУ‰ВО¸, ‚ ЪУ ‚рВПfl Н‡Н УМ‡ ‰УОКМ‡ ·˚Ъ¸ МВОЛМВИМУИ) Л Ъ. Ф. йТУ·ВММУ ФУ‰- ‚ВрКВМ˚ ‡‚ЪУНУррВОflˆЛЛ ‰‡ММ˚В ‚рВПВММ˚ı рfl‰У‚ ФУН‡Б‡ЪВОВИ.
ᇂЛТЛПУТЪ¸ ПВК‰Ы УТЪ‡ЪН‡ПЛ УФЛТ˚‚‡ВЪТfl Ъ‡НКВ Т ФУПУ˘¸˛ Ыр‡‚МВМЛfl рВ„рВТТЛЛ:
εi = ρεi−1 + zi ,
„‰Â ÓÒÚ‡ÚÓÍ εi ̇ıÓ‰ËÚÒfl ÔÓ‰ ‚ÎËflÌËÂÏ ‚Â΢ËÌ˚ ÓÒÚ‡Ú͇ Ôр‰˚‰Û-
˘Â„Ó Ì‡·Î˛‰ÂÌËfl εi-1 Л Н‡НУ„У-ОЛ·У ЪВНЫ˘В„У БМ‡˜ВМЛfl ТОЫ˜‡ИМУИ ФВрВПВММУИ zi. ùÚ‡ ÙÓрχ ÙÛÌ͈ËË Ì‡Á˚‚‡ÂÚÒfl ‡‚ЪУрВ„рВТТЛУМУИ ЩЫМНˆЛВИ ФВр‚У„У ФУрfl‰Н‡ (Äê(1)), Ú. Í. ÚÓθÍÓ Ó‰ËÌ Ôр‰¯ÂÒÚ-
‚Ы˛˘ЛИ ФВрЛУ‰ Ы˜ЪВМ ФрЛ УˆВМЛ‚‡МЛЛ Б‡‚ЛТЛПУТЪЛ УТЪ‡ЪНУ‚.
З ТОЫ˜‡В, НУ„‰‡ ФрВ‰ФУО‡„‡ВЪТfl Б‡‚ЛТЛПУТЪ¸ ЪВНЫ˘В„У УТЪ‡ЪН‡ УЪ ‚ВОЛ˜ЛМ УТЪ‡ЪНУ‚ ‰‚Ыı Л ·УОВВ ФрВ‰¯ВТЪ‚Ы˛˘Лı ФВрЛУ‰У‚, ‡‚ЪУрВ„рВТТЛУМ˚В ЩЫМНˆЛЛ ЛПВ˛Ъ ТОВ‰Ы˛˘ЛИ ‚Л‰:
εi = ρεi−1 +ρεi−2 +... +ρεi−s + zi .
кВ„рВТТЛУММ‡fl ПУ‰ВО¸ ФУБ‚УОflВЪ ФУОЫ˜ЛЪ¸ МВТПВ˘ВММЫ˛ УˆВМНЫ Т М‡ЛПВМ¸¯ВИ ‰ЛТФВрТЛВИ ЪУ„‰‡, НУ„‰‡ УТЪ‡ЪНЛ МВБ‡‚ЛТЛП˚ ‰рЫ„
147

УЪ ‰рЫ„‡. дУ„‰‡ ТЫ˘ВТЪ‚ЫВЪ ‡‚ЪУНУррВОflˆЛfl УТЪ‡ЪНУ‚, ЪУ НУ˝ЩЩЛˆЛВМЪ˚ рВ„рВТТЛЛ МВ ТПВ˘ВМ˚, МУ ТЪ‡М‰‡рЪМ˚В У¯Л·НЛ ·Ы‰ЫЪ МВ‰У- УˆВМВМ˚, Л ФрУ‚ВрНЛ НУ˝ЩЩЛˆЛВМЪУ‚ рВ„рВТТЛЛ ·Ы‰ЫЪ МВМ‡‰ВКМ˚.
СОfl ФрУ‚ВрНЛ М‡ М‡ОЛ˜ЛВ ‡‚ЪУНУррВОflˆЛЛ УТЪ‡ЪНУ‚ ‚ ПУ‰ВОЛ ПУКМУ ФУТЪрУЛЪ¸ „р‡ЩЛН Б‡‚ЛТЛПУТЪЛ УТЪ‡ЪНУ‚ УЪ ‚рВПВМЛ Л УФрВ- ‰ВОЛЪ¸ ‡‚ЪУНУррВОflˆЛ˛ ‚ЛБЫ‡О¸МУ ОЛ·У ‚УТФУО¸БУ‚‡Ъ¸Тfl НрЛЪВрЛВП С‡р·ЛМ‡-мУЪТУМ‡:
|
n |
(ei −ei−1 )2 |
|
|
∑ |
|
|
DW = |
i=2 |
|
. |
|
n |
||
|
|
|
|
|
|
∑ei2 |
|
|
|
i=2 |
|
лУ„О‡ТМУ ˝ПФЛрЛ˜ВТНУПЫ Фр‡‚ЛОЫ, ВТОЛ НрЛЪВрЛИ С‡р·ЛМ‡-мУЪ- ТУМ‡ р‡‚ВМ 2, ЪУ МВ ТЫ˘ВТЪ‚ЫВЪ ФУОУКЛЪВО¸МУИ ‡‚ЪУНУррВОflˆЛЛ, ВТОЛ УМ р‡‚ВМ 0, ЪУ ЛПВВЪ ПВТЪУ ТУ‚Вр¯ВММ‡fl ФУОУКЛЪВО¸М‡fl ‡‚ЪУНУррВОflˆЛfl, ‡ ВТОЛ УМ р‡‚ВМ 4, ЪУ ЛПВВЪ ПВТЪУ ТУ‚Вр¯ВММ‡fl УЪрЛˆ‡ЪВО¸М‡fl ‡‚ЪУНУррВОflˆЛfl. й‰М‡НУ ‰‡ММ˚И НрЛЪВрЛИ ЛПВВЪ ‚˚·УрУ˜МУВ р‡ТФрВ- ‰ВОВМЛВ, ·‡БЛрЫ˛˘ВВТfl М‡ ТФВˆЛ‡О¸МУИ Ъ‡·ОЛˆВ32. щЪУ ‚˚·УрУ˜МУВ р‡ТФрВ‰ВОВМЛВ У·О‡‰‡ВЪ ‰‚ЫПfl НрЛЪЛ˜ВТНЛПЛ БМ‡˜ВМЛflПЛ dL Ë dU.
З ФрУˆВТТВ ФрУ‚ВрНЛ ПУ‰ВОЛ М‡ ‡‚ЪУНУррВОflˆЛ˛ УТЪ‡ЪНУ‚ Т ФУПУ˘¸˛ ˝ЪУ„У НрЛЪВрЛfl ФрУ‚Врfl˛ЪТfl ТОВ‰Ы˛˘ЛВ „ЛФУЪВБ˚:
H0: ÌÂÚ ‡‚ÚÓÍÓррÂÎflˆËË, ÂÒÎË dU ≤ DW ≤ 4 – dU;
H1: ФУОУКЛЪВО¸М‡fl ‡‚ЪУНУррВОflˆЛfl ФрЛ DW < dL; ÓÚрˈ‡ÚÂθ- ̇fl ‡‚ÚÓÍÓррÂÎflˆËfl ÔрË DW > 4 – dL.
д ТУК‡ОВМЛ˛, ‚ ТУТЪ‡‚В ‰‡ММУ„У р‡ТФрВ‰ВОВМЛfl ТЫ˘ВТЪ‚Ы˛Ъ БУМ˚ МВУФрВ‰ВОВММУТЪЛ, „‰В рВБЫО¸Ъ‡Ъ˚ ПУ„ЫЪ ЫН‡Б˚‚‡Ъ¸ Н‡Н М‡ М‡- ОЛ˜ЛВ, Ъ‡Н Л М‡ УЪТЫЪТЪ‚ЛВ ‡‚ЪУНУррВОflˆЛЛ УТЪ‡ЪНУ‚:
dL < DW < dU , или 4 – dU < DW < 4 – dL.
СОfl ФрЛПВМВМЛfl НрЛЪВрЛfl С‡р·ЛМ‡-мУЪТУМ‡ ТЫ˘ВТЪ‚Ы˛Ъ МВНУЪУр˚В У„р‡МЛ˜ВМЛfl.
ÇÓ-ÔÂð‚˚ı, УМ МВФрЛПВМЛП Н ПУ‰ВОflП Т О‡„У‚˚ПЛ БМ‡˜ВМЛflПЛ Б‡‚ЛТЛПУ„У ФрЛБМ‡Н‡, ‚НО˛˜‡ВП˚ПЛ ‚ ПУ‰ВО¸ Н‡Н Щ‡НЪУр М‡рfl‰Ы Т
32 щЪЫ Ъ‡·ОЛˆЫ ПУКМУ М‡ИЪЛ ‚ Ы˜В·МЛНВ СУЫ„ВрЪЛ д. З‚В‰ВМЛВ ‚ ˝НУМУПВЪрЛНЫ: иВр. Т ‡М„О. е.: азокД-е, 1999. л. 372–373.
148

ФрУ˜ЛПЛ (‡‚ЪУрВ„рВТТЛУМ˚В ПУ‰ВОЛ). СОfl ЪВТЪЛрУ‚‡МЛfl М‡ ‡‚ЪУНУррВОflˆЛ˛ ‚ Ъ‡НЛı ПУ‰ВОflı ЛТФУО¸БЫВЪТfl h-НрЛЪВрЛИ С‡р·ЛМ‡33.
ÇÓ-‚ÚÓð˚ı, ÔрË ÔрÓ‚ÂрÍ ̇ ‡‚ÚÓÍÓррÂÎflˆË˛ ·ÓΠ‚˚ÒÓÍËı, ˜ÂÏ ÔÂр‚˚È, ÔÓрfl‰ÍÓ‚ ÒΉÛÂÚ ÔрËÏÂÌflÚ¸ ËÌ˚ ÏÂÚÓ‰˚34.
Ç-ÚðÂÚ¸Ëı, НрЛЪВрЛИ С‡р·ЛМ‡-мУЪТУМ‡ ‰‡ВЪ ‰УТЪУ‚ВрМ˚В рВБЫО¸Ъ‡Ъ˚ ЪУО¸НУ ‚ УЪМУТЛЪВО¸МУ ·УО¸¯Лı ‚˚·УрН‡ı, МВ ПВМВВ 15–20 М‡·О˛‰ВМЛИ.
СОfl ЪУ„У ˜ЪУ·˚ рВ¯ЛЪ¸ ФрУ·ОВПЫ ‡‚ЪУНУррВОflˆЛЛ, ТМ‡˜‡О‡ ТОВ- ‰ЫВЪ р‡ТТПУЪрВЪ¸ ‚УБПУКМУТЪ¸ ЛТНО˛˜ВМЛfl ФВрВПВММ˚ı ЛБ ПУ‰ВОЛ ЛОЛ ЛБПВМВМЛВ ЩУрП˚ ЩЫМНˆЛУМ‡О¸МУИ Б‡‚ЛТЛПУТЪЛ рВБЫО¸ЪЛрЫ˛- ˘ВИ ФВрВПВММУИ УЪ ФВрВПВММ˚ı-Щ‡НЪУрУ‚. ЦТОЛ ˝ЪУ МВ ФрЛ‚У‰ЛЪ Н ЫТФВ¯МУПЫ ЛТНО˛˜ВМЛ˛ ‡‚ЪУНУррВОflˆЛЛ УТЪ‡ЪНУ‚, ПУКМУ ФрЛПВМЛЪ¸ ФрУˆВ‰ЫрЫ дУНр‡М‡-йрН‡ЪЪ‡35.
ЦТОЛ МВНУЪУр˚В ЛОЛ ‚ТВ МВБ‡‚ЛТЛП˚В ФВрВПВММ˚В ‚ ПУ‰ВОЛ ПМУКВТЪ‚ВММУИ рВ„рВТТЛЛ fl‚Оfl˛ЪТfl ‚˚ТУНУНУррВОЛрУ‚‡ММ˚ПЛ, ЪрЫ‰МУ ‚ р‡ПН‡ı рВ„рВТТЛУММУИ ПУ‰ВОЛ р‡Б„р‡МЛ˜ЛЪ¸ Лı УЪ‰ВО¸М˚В ‚ОЛflМЛfl М‡ Y. щЪУ Ъ‡НКВ ПУКВЪ УБМ‡˜‡Ъ¸ М‡ОЛ˜ЛВ ПВК‰Ы ‚˚ТУНУНУррВОЛрУ‚‡ММ˚ПЛ МВБ‡‚ЛТЛП˚ПЛ ФВрВПВММ˚ПЛ ПЫО¸ЪЛНУООЛМВ‡р- МУТЪЛ — ОЛМВИМУИ Б‡‚ЛТЛПУТЪЛ, Ъ. В. ‚УБ‰ВИТЪ‚Лfl У‰МУ„У Щ‡НЪУр‡ М‡ ‰рЫ„УИ. З˚ТУНУНУррВОЛрУ‚‡ММ˚В ФВрВПВММ˚В ‰ВИТЪ‚Ы˛Ъ ‚ У‰МУП
М‡Фр‡‚ОВМЛЛ, ‚ рВБЫО¸Ъ‡ЪВ ˜В„У ПУ‰ВО¸ МВ ПУКВЪ ЛБУОЛрУ‚‡Ъ¸ ‚ОЛflМЛВ Н‡К‰УИ ЛБ ФВрВПВММ˚ı-Щ‡НЪУрУ‚ М‡ рВБЫО¸Ъ‡Ъ. ирЛ ПЫО¸- ЪЛНУООЛМВ‡рМУТЪЛ НУ˝ЩЩЛˆЛВМЪ˚ рВ„рВТТЛЛ МВТЪ‡·ЛО¸М˚ ФУ Лı
ТЪ‡ЪЛТЪЛ˜ВТНУИ БМ‡˜ЛПУТЪЛ, ‚ВОЛ˜ЛМВ Л БМ‡НЫ, ‡ ТЪ‡ОУ ·˚Ъ¸ — МВ- М‡‰ВКМ˚. бМ‡˜ВМЛfl R2 ÏÓ„ÛÚ ·˚Ú¸ ‚˚ÒÓÍË, ÌÓ Òڇ̉‡рÚÌ˚ ӯ˷ÍË Ú‡ÍÊ ‚˚ÒÓÍË, ÓÚÒ˛‰‡ t-НрЛЪВрЛЛ П‡О˚, УЪр‡К‡fl МВ‰УТЪ‡ЪУН БМ‡˜Л- ПУТЪЛ.
дУ˝ЩЩЛˆЛВМЪ˚ ЛМЪВрНУррВОflˆЛЛ (Ъ. В. Ф‡рМУИ НУррВОflˆЛЛ ПВ- К‰Ы У·˙flТМfl˛˘ЛПЛ ФВрВПВММ˚ПЛ) ФУБ‚УОfl˛Ъ ЛТНО˛˜‡Ъ¸ ЛБ ПУ‰ВОЛ
‰Ы·ОЛрЫ˛˘ЛВ Щ‡НЪУр˚. л˜ЛЪ‡ВЪТfl, ˜ЪУ ‰‚В ФВрВПВММ˚В fl‚МУ НУООЛМВ‡рМ˚, Ú. Â. М‡ıУ‰flЪТfl ПВК‰Ы ТУ·УИ ‚ ОЛМВИМУИ Б‡‚ЛТЛПУ-
33лП., М‡ФрЛПВр: щНУМУПВЪрЛН‡: м˜В·. / иУ‰ рВ‰. а. а. ЦОЛТВВ‚УИ. е.: оЛМ‡М- Т˚ Л ТЪ‡ЪЛТЪЛН‡, 2001. л. 325–330.
34лП., М‡ФрЛПВр: СУЫ„ВрЪЛ д. З‚В‰ВМЛВ ‚ ˝НУМУПВЪрЛНЫ: иВр. Т ‡М„О. е.: азокД-е, 1999. л. 239–240.
35ëÏ.: ÑÓÛ„ÂрÚË ä. í‡Ï ÊÂ. ë. 222–223; щНУМУПВЪрЛН‡: м˜В·. / иУ‰ рВ‰. а. а. ЦОЛТВВ‚УИ. л. 281.
149

ÒÚË, ÂÒÎË Ô‡рÌ˚È ÍÓ˝ÙÙˈËÂÌÚ ÍÓррÂÎflˆËË ÏÂÊ‰Û ÌËÏË р‡‚ÂÌ ËÎË Ôр‚˚¯‡ÂÚ 0,836.
иУТНУО¸НЫ У‰МЛП ЛБ ЫТОУ‚ЛИ ФУТЪрУВМЛfl Ыр‡‚МВМЛfl ПМУКВТЪ- ‚ВММУИ рВ„рВТТЛЛ fl‚ОflВЪТfl МВБ‡‚ЛТЛПУТЪ¸ Щ‡НЪУрУ‚, НУООЛМВ‡р- МУТЪ¸ Щ‡НЪУрУ‚ М‡рЫ¯‡ВЪ ˝ЪУ ЫТОУ‚ЛВ. ЦТОЛ Щ‡НЪУр˚ fl‚МУ НУООЛМВ‡рМ˚, ЪУ У‰ЛМ ЛБ МЛı рВНУПВМ‰ЫВЪТfl ЛТНО˛˜ЛЪ¸ ЛБ рВ„рВТТЛЛ. ирВ‰ФУ˜ЪВМЛВ ФрЛ ˝ЪУП УЪ‰‡ВЪТfl МВ Щ‡НЪУрЫ, ·УОВВ ЪВТМУ Т‚flБ‡М- МУПЫ Т рВБЫО¸Ъ‡ЪУП, ‡ ЪУПЫ Щ‡НЪУрЫ, НУЪУр˚И ФрЛ ‰УТЪ‡ЪУ˜МУ ЪВТМУИ Т‚flБЛ Т рВБЫО¸Ъ‡ЪУП ЛПВВЪ М‡ЛПВМВВ ЪВТМЫ˛ Т‚flБ¸ Т ‰рЫ„ЛПЛ Щ‡НЪУр‡ПЛ.
З УЪМУ¯ВМЛЛ ПЫО¸ЪЛНУООЛМВ‡рМУТЪЛ ПУ„ЫЪ ·˚Ъ¸ ФрВ‰ФрЛМflЪ˚ МВНУЪУр˚В ПВр˚:
1)ЛТНО˛˜ВМЛВ ЛБ ПУ‰ВОЛ ЪВı Щ‡НЪУрУ‚, НУЪУр˚В fl‚Оfl˛ЪТfl ‚˚- ТУНУНУррВОЛрУ‚‡ММ˚ПЛ Т УТЪ‡О¸М˚ПЛ. й‰М‡НУ, ‚УБПУКМУ, ˜ЪУ ‰‡М- М˚В ФВрВПВММ˚В ·˚ОЛ ‚НО˛˜ВМ˚ ‚ ПУ‰ВО¸ ‚ ТУУЪ‚ВЪТЪ‚ЛЛ Т рВБЫО¸- Ъ‡Ъ‡ПЛ Ъ˘‡ЪВО¸МУ„У ФрВ‰‚‡рЛЪВО¸МУ„У Н‡˜ВТЪ‚ВММУ„У ЪВУрВЪЛНУ- ˝НУМУПЛ˜ВТНУ„У ‡М‡ОЛБ‡, ‡ БМ‡˜ЛЪ ·Ы‰ВЪ МВ ТУ‚ТВП УФр‡‚‰‡МУ ЛТНО˛˜‡Ъ¸ Лı ЪУО¸НУ ‰Оfl ЪУ„У, ˜ЪУ·˚ ЫОЫ˜¯ЛЪ¸ ТЪ‡ЪЛТЪЛ˜ВТНЛВ рВБЫО¸Ъ‡Ъ˚;
2)Ы‚ВОЛ˜ВМЛВ У·˙ВП‡ ‚˚·УрНЛ ФУ ФрЛМˆЛФЫ: ˜ВП ·УО¸¯В ‰‡М- М˚ı, ЪВП ПВМ¸¯В ‰ЛТФВрТЛЛ УˆВМУН езд. ирУ·ОВП‡ ‚ рВ‡ОЛБ‡ˆЛЛ ˝ЪУ„У ‚‡рЛ‡МЪ‡ — МВУ·ıУ‰ЛПУ М‡ИЪЛ ‰УФУОМЛЪВО¸М˚В ‰‡ММ˚В;
3)ФрВУ·р‡БУ‚‡МЛВ Щ‡НЪУрУ‚ Ъ‡НЛП У·р‡БУП, ˜ЪУ·˚ ЫПВМ¸¯ЛЪ¸ НУррВОflˆЛ˛ ПВК‰Ы МЛПЛ, М‡ФрЛПВр ФВрВıУ‰ УЪ ЛТıУ‰М˚ı ФВрВПВМ- М˚ı Н Лı ОЛМВИМ˚П НУП·ЛМ‡ˆЛflП, МВ НУррВОЛрУ‚‡ММ˚П ‰рЫ„ Т ‰рЫ- „УП (ПВЪУ‰ „О‡‚М˚ı НУПФУМВМЪ37).
ирУ„МУБЛрУ‚‡МЛВ М‡ УТМУ‚В ˝НУМУПВЪрЛ˜ВТНЛı ПУ‰ВОВИ (М‡ ФрЛПВрВ ПУ‰ВОЛ ЛБ У‰МУ„У Ыр‡‚МВМЛfl)
З ФрУ„МУБМ˚ı р‡Т˜ВЪ‡ı ФУ Ыр‡‚МВМЛ˛ рВ„рВТТЛЛ УФрВ‰ВОflВЪТfl ФрВ‰ТН‡Б˚‚‡ВПУВ БМ‡˜ВМЛВ Yi+l Í‡Í ÚӘ˜Ì˚È ÔрÓ„ÌÓÁ ‚Â΢ËÌ˚ Y ÔрË Á‡‰‡ÌÌ˚ı x1i+1 , x2i+1 , ..., xmi+1 ФЫЪВП ФУ‰ТЪ‡МУ‚НЛ ‰‡ММ˚ı БМ‡˜ВМЛИ МВБ‡‚ЛТЛП˚ı ФВрВПВММ˚ı ‚ Ыр‡‚МВМЛВ рВ„рВТТЛЛ. й‰М‡НУ ЪУ˜В˜М˚И
36щНУМУПЛНУ-П‡ЪВП‡ЪЛ˜ВТНЛВ ПВЪУ‰˚ Л ФрЛНО‡‰М˚В ПУ‰ВОЛ: м˜В·. ФУТУ·ЛВ ‰Оfl ‚ЫБУ‚ / иУ‰ рВ‰. З. З. оВ‰УТВВ‚‡. е.: ызана, 1999. л. 268.
37лП., М‡ФрЛПВр: щНУМУПВЪрЛН‡: м˜В·. / иУ‰ рВ‰. а. а. ЦОЛТВВ‚УИ. е.: оЛМ‡М- Т˚ Л ТЪ‡ЪЛТЪЛН‡, 2001. л. 314–319.
150
