
posobie5_1mua
.pdf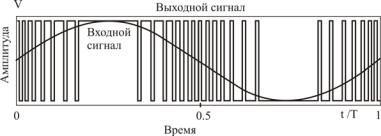
290
ления на низких частотах ослабляется, а на высоких частотах при низком коэффициенте усиления ослабления не будет.
Анализ линеаризованной модели дельта-сигма модулятора проведем используя z-преобразование полагая, что входной сигнал дискретизирован по времени. При линеаризации нелинейный компаратор, заменяется усилителем и источника шума квантования E(z), рис.10.1,б. В таком случае имеем
y(z) = (x(z) − y(z))H(z) + E(z) = STF (z)x(z) + NNF (z)E(z) , (10.1)
где: S (z) ≡ |
y(z) |
= |
|
H(z) |
– передаточная функция сигнла, (10.2) |
||||||||
|
|
|
|
|
|||||||||
TF |
|
x(z) |
|
1+ H(z) |
|
|
|||||||
|
|
|
|
|
|||||||||
NTF (z) ≡ |
y(z) |
= |
|
|
|
|
1 |
– передаточная функция шума. |
(10.3) |
||||
E(z) |
1 |
+ H(z) |
|||||||||||
|
|
|
|
|
|||||||||
Из (10.2) и (10.3) следует, что если H(z) достаточно велико в диапазоне частот сигнала(0 – fcB ),B то в том же диапазоне STF 1 и NTF 0.
Вход фильтра – разница между входным сигналом x(n) и цифровым значением выхода y(n). Поскольку y(n) принимает значение ±1, то разница может быть велика. Однако, если система стабильна, то в силу большого прямого коэффициента усиления на нулевой частоте среднее значение на входе фильтра (а значит и на выходе модулятора) близко к нулю.
Выходной сигнал дельта-сигма модулятора – поток двоичных имульсов, рис.10.2.
Рис.10.2. Выходной сигнал дельта-сигма модулятора
291
При входном сигнале близком к краям диапазона (±1) преобладают импульсы той же полярности (если диапазон 0 –1, то импульсы однополярны). При входных сигналах близких к средине диапазона – скважность выходных импульсов близка к двум.
Усреднение выходного сигнала – происходит в цифровом фильтре (дециматоре), который является составной частью ∆Σ АЦП и следует после модулятора (Рис.8.10).
Шумы квантования. Шум квантования в ∆Σ-модуляторе за счет передискретизации и наличии ФНЧ существенно отличается от белого шума.
Пусть в качестве ФНЧ использован фильтр n-го порядка, у которого все полюса при нулевой частоте, т.е. для него STFB ≈B (1–z-P 1)P nP .P Тогда на
выходе модулятора мощность шума квантования E2n составит
|
|
|
|
|
|
|
|
2 |
|
fc |
(1 |
− z−1 )2n |
|
|
|
|
2 |
fc |
|
|
−2 |
π |
f |
2n |
|
||||
En2 = E2 |
|
∫ |
|
df = E2 |
∫ |
1 |
− e |
|
|
fs |
df |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f |
s |
0 |
|
|
|
|
|
|
|
|
f |
s |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,(10.4) |
|||||
|
|
|
|
π |
2n |
|
|
|
2fc |
2n+1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2n |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
fs |
|
|
|
|
|
|
|
|
|
|||||||||||||||
где E2 – полная мощность шума квантования (1.3).
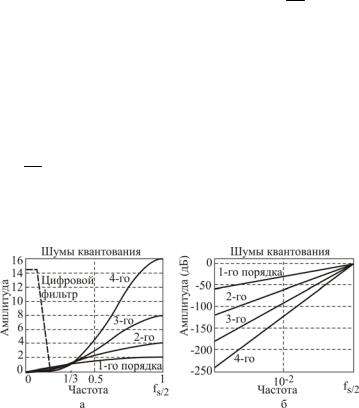
Из (10.4) следует быстрое снижение шумов квантования в полосе частот сигнала при fcB <<B fsB B с возрастанием порядка ∆Σ-модулятора, рис. 10.3.
Рис.10.3. Зависимость шумов квантования от частоты дискретизации: а – линейная шкала; б – логарифмическая шкала

292
Как следует из (10.4) и проиллюстрировано рис.10.3 в ∆Σ- модуляторе происходит перенос шумов из низкочастотной части спектра в высокочастотную его часть. Высокочастотные шумы в потоке сигналов можно отфильтровать цифровым фильтром.
Снижение шумов квантования в полосе частот сигнала увеличивает динамический диапазон преобразователя. Проделав выкладки аналогичные (1.5), имеем
|
|
2 |
|
|
|
F |
|
||||
|
|
|
|
|
|
|
|
|
|
||
SNR =10 log |
|
2 |
|
= 6.02 N +1.76 +10(2n +1)log M |
|
|
En |
|
дБ. (10.5) |
||
− 20n log π +10log(2n +1)
где: N – разрядность АЦП, если используется компаратор N=1;
M = 2ffsc – коэффициент передискретизации.
Из (10.5) следует, что удвоение частоты выборки в модуляторе первого порядка улучшает динамический диапазон на 9 дБ (1.5 бит/октаву), а в модуляторе второго порядка на 15 дБ (2.5 бит/октаву).
10.2. Варианты ∆Σ-модуляторов
∆Σ-модулятор первого порядка. Модулятор первого порядка,
рис.10.1, может быть реализован на ПК-схемах, рис.10.4.
293
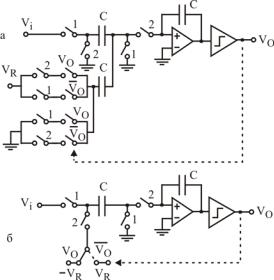
Рис.10.4. ∆Σ-модулятор первого порядка на ПК:
а – с одним опорным источником; б – с двумя опорными источниками.
Они содержат компараторы, ОУ, ключи и конденсаторы. Во время первой фазы входной сигнал и сигнал обратной связи накапливаются на входных емкостях ОУ, а во время второй фазы они передаются на интегрирующий конденсатор в цепи обратной связи ОУ, рис. 10.4,б.
Наиболее критичной в модуляторе является аналоговая операция вычитания выходного сигнала из входного. Именно ее точность определяет точность модулятора. Для повышения точности необходимо использовать стабилизированное опорное напряжение VRB .B В точность операции вносит вклад и шум переключения конденсаторов. Для его уменьшения емкости конденсаторов должны быть достаточно большими.
Для вычитания можно использовать два входных конденсатора и одно опорное напряжение, рис.10.4,а, или один конденсатор и два опорных напряжения, рис10.4,б.
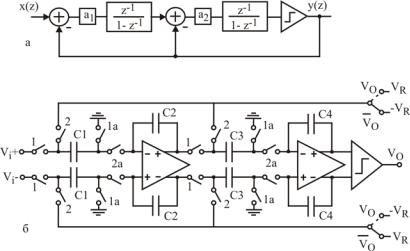
Модулятор второго порядка. Модулятор второго порядка содержит два интегратора, рис.10.5,а. Его поведение определяется величинами коэффициентов a1B B и а2B .B Малые значения коэффициентов ограничивают полосу пропускания, а большие могут привести к неустойчивости работы.
294
Из анализа линеаризованной модели вытекает необходимое условие а1B <4/5B .
В ПК-схемах коэффициенты задаются отношением емкостей. Так а1B =B С1/С2, а2B =B С3/С4 в схеме на рис.10.5,б.
Рис.10.5 ∆Σ-модулятор второго порядка: а – эквивалентная схема; б – симметричный вариант на ПК
Одним из способов повышения точности работы модуляторов на ПК, является использование симметричных (дифференциальных) схем, рис.10.5,б. В этой схеме использована модифицированная система тактирования. Вспомогательные тактовые импульсы 1а и 2а начинаются и заканчиваются немного раньше основных таковых импульсов 1 и 2.
Модуляторы высоких порядков. При использовании модулято-
ров высоких порядках необходимо решать достаточно сложную проблему устойчивости. Наиболее часто применяют архитектуру с использованием опережающих прямых и локальных обратных связей, рис.10.6.
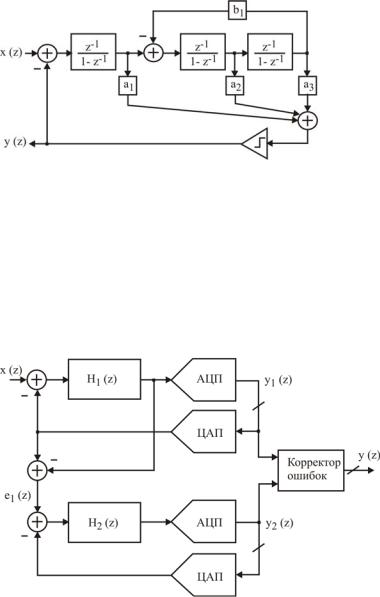
295
Рис.10.6. ∆Σ-модулятор третьего порядка
Существуют различные полуэмпирические методы синтеза подобных модуляторов.
Каскадированные модуляторы. Каскадированные (мэш)
модуляторы позволяют снять проблему устойчивости модуляторов высокого порядка за счет использования каскадов, включающих устойчивые модуляторы (первого или второго порядка), рис.10.7. Однако они налагают более высокие требования на точность согласования параметров используемых элементов.
Рис.10.7 Каскадированный ∆Σ-модулятор

296
Многобитовые модуляторы. В многобитовых модуляторах, рис.8.10, используют многоразрядные АЦП и ЦАП.
Многобитовые модуляторы более устойчивы, чем однобитовые, предъявляют меньшие требования к цифровым фильтрам. Однако у них возникает проблема нелинейности, обусловленная неидеальностью АЦП и ЦАП, которая отсутствует в однобитных модуляторах. Используют и каскадированные многобитные модуляторы, рис.10.7.
Сравнение модуляторов. Основные параметры модуляторов приведены в табл.10.1
Сравнительные параметры модуляторов |
|
Таблица 10.1 |
||||
Тип модуля- |
Раз- |
SNR(M) |
Ли- |
Простота |
Устой- |
Про- |
тора |
ряд- |
|
ней- |
модуля- |
чи- |
стота |
|
ность |
|
ность |
тора |
вость |
ЦФ |
Низкого по- |
1 |
– |
– |
+ |
+ |
+ |
рядка |
1 |
|
|
|
|
|
Высокого |
+ |
+ |
+ |
– |
+ |
|
порядка |
1 |
|
|
|
|
|
Каскадиро- |
+ |
– |
– |
+ |
– |
|
ванный |
4–8 |
|
|
|
|
|
Многобитный |
+ |
– |
– |
+ |
– |
|
10.3. Цифровые фильтры
Задача цифровой фильтрации – преобразование высокочастотного потока однобитных (или многобитных, в случае многобитных модуляторов) данных в низкочастотный поток данных заданной разрядности (децимация) с эффективным подавлением шумов квантования. Этот процесс по существу является усреднением с прореживанием.
Цифровой фильтр(ЦФ) должен обрабатывать высокочастотный сигнал в реальном времени, должен иметь спад АЧХ вне рабочей полосы, согласованный с порядком модулятора (т.е. спад, не меньший,7 чем подъем АЧХ шумов квантования модулятора), обладать линейной фазовой характеристикой.
Цифровой фильтр разрабатываться с учетом требований его интегральной реализации: минимизации площади (количества транзисторов) и потребляемой мощности при заданном быстродействии.
Для интегрального выполнения пригоден трансверсальный (FIR) фильтр, рис.10.8.

297
Рис.10.8. Трансверсальный фильтр N-го порядка
Его достоинством является потенциальная устойчивость – отсутствие полюсов частотной передаточной характеристики. Его недостаток – большие аппаратные затраты, связанные с операцией умножения.
В ряде случаев используется и типичный для аналоговой техники рекурсивный (IIR) фильтр. Его достоинство – меньшее количество умножений для получения заданного спада АЧХ ФНЧ. Недостаток – проблема стабильности фильтра высокого порядка.
Рис.10.9. Рекурсивный фильтр второго порядка
Простейший и наиболее экономичный фильтр для подавления высокочастотных шумов квантования – фильтр скользящего среднего – “синк-фильтр” (sinc-фильтр). Это трансверсальный (FIR) фильтр все коэффициенты которого одинаковы и для фильтра N-го порядка равны 1/N,
рис.10.10,а.
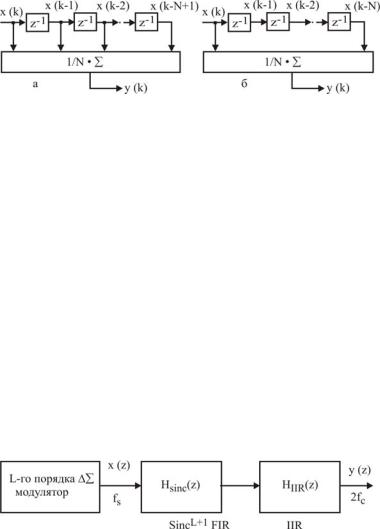
298
Рис.10.10. Фильтр скользящего среднего:
а– с комбинационным сумматором; б – с накапливающим сумматором
Втаком варианте для сложения N задержанных кодов использован комбинационный сумматор. Накапливающий сумматор в его составе позволяет ограничиться сложением только двух кодов, рис.10.10,б, поскольку при добавлении последнего и вычитания сдвинутого на N тактов
всумматоре накапливается (скользящая) сумма N кодов.
Если на входе «синк-фильтра» двоичные коды, а N степень двойки, то сумматор допускает замену на реверсивный счетчик.
Но передаточная АЧХ простого «синк-фильтра» имеет спад порядка 20 дБ на декаду, что недостаточно для фильтрации потоков от модуляторов порядка L. В этом случае используют последовательное соединение L+1 таких фильтров (SincL+1P P FIR). Оно обеспечивает спад 20L дБ на декаду, но его АЧХ сохраняет периодические выбросы в области заграждения и некоторый спад в области пропускания. Поэтому во многих случаях, где недопустимы такие искажения, «синк-фильтр» используется с одним или несколькими дополнительными цифровыми фильтрами. Это может быть IIR фильтр, рис.10.11, с прореживанием (снижением частоты) выходных кодов до частоты Найквиста.
Рис.10.11. Блок-схема ЦФ ∆Σ-АЦП с дополнительным IIR фильтром
Чаще используют FIR фильтр или даже несколько FIR фильтров, рис.10.12,а. выполняющих выравнивание АЧХ. Компенсационный фильтр выполняет подъем передаточной характеристики в области пропускания, а полуполосовой FIR – ослабление в области заграждения, рис.10.12,б.
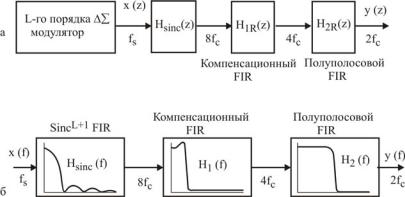
299
Рис.10.12. Блок-схема ЦФ ∆Σ-АЦП с дополнительным FIR фильтром: а – z-представление; б – частотное представление
Выход первого каскада многокаскадного «синк-фильтра» представляет собой не однобитовый поток, а поток многоразрядных кодов. Поэтому последующие каскады должны содержать N регистров для требуемой задержки, что увеличивает аппаратурные затраты. Для их снижения используют модифицированную архитектуру (и алгоритм работы) фильтра.
Передаточная функция «синк-фильтра» N-го порядка имеет вид
|
1 |
|
1− z |
−N L+1 |
|
|||
Hsin k−N (z) = |
|
|
|
|
(10.6) |
|||
|
L+1 |
|
|
−1 |
||||
N |
|
1− z |
. |
|||||
|
|
|
|
|
|
|||
Числитель и знаменатель (10.6) можно представить в виде сомножителей
|
|
1 |
L+1 |
|
−N |
|
L+1 |
1 |
|
|||
H |
sin k−N |
(z) = |
|
|
|
|
(1− z |
|
) |
|
|
(10.7) |
1 |
− z−1 |
|
|
NL+1 |
||||||||
|
|
|
|
|
|
|
|
|||||
Непосредственная реализация выражения (10.7) приводит к архитектуре фильтра включающей (L+1) последовательно включенный интегратор и (L+1) последовательно включенный дифференциатор, работающие на в M раз более низкой частоте, рис.10.13.
