ЭКОНОМЕТРИКА 1
.docx
![]() ЗАДАНИЕ
N 1
сообщить
об ошибке
Тема:
Проверка статистической значимости
эконометрической модели
ЗАДАНИЕ
N 1
сообщить
об ошибке
Тема:
Проверка статистической значимости
эконометрической модели
Начало формы




Конец формы
Проверку статистической значимости построенной эконометрической модели на основе F-критерия осуществляют с использованием …
|
|
|
|
статистических гипотез |
|
|
|
|
стандартизованных переменных |
|
|
|
|
системы нормальных уравнений |
|
|
|
|
коллективных гипотез |
![]() ЗАДАНИЕ
N 2
сообщить
об ошибке
Тема:
Оценка тесноты связи
ЗАДАНИЕ
N 2
сообщить
об ошибке
Тема:
Оценка тесноты связи
Начало формы




Конец формы
Для
регрессионной модели вида
![]() построена
на координатной плоскости совокупность
точек с координатами
построена
на координатной плоскости совокупность
точек с координатами
![]() ,
данное графическое отображение
зависимости называется …
,
данное графическое отображение
зависимости называется …
|
|
|
|
полем корреляции |
|
|
|
|
параметрами уравнения |
|
|
|
|
случайными факторами |
|
|
|
|
множественной регрессией |
![]() ЗАДАНИЕ
N 3
сообщить
об ошибке
Тема:
Оценка качества подбора уравнения
ЗАДАНИЕ
N 3
сообщить
об ошибке
Тема:
Оценка качества подбора уравнения
Начало формы




Конец формы
Для
регрессионной модели парной регрессии
рассчитано значение коэффициента
детерминации
![]() .
Тогда долю остаточной дисперсии зависимой
переменной характеризует величина …
.
Тогда долю остаточной дисперсии зависимой
переменной характеризует величина …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 4
сообщить
об ошибке
Тема:
Оценка значимости параметров
эконометрической модели
ЗАДАНИЕ
N 4
сообщить
об ошибке
Тема:
Оценка значимости параметров
эконометрической модели
Начало формы




Конец формы
Если параметр эконометрической модели не является статистически значимым, то соответствующая независимая переменная …
|
|
|
|
не оказывает влияния на моделируемый показатель (зависимую переменную) |
|
|
|
|
оказывает статистически значимое влияние на моделируемый показатель (зависимую переменную) |
|
|
|
|
тесно связан с зависимой переменной |
|
|
|
|
оказывает основное (доминирующее) влияние на зависимую переменную |
![]() ЗАДАНИЕ
N 5
сообщить
об ошибке
Тема:
Обобщенный метод наименьших квадратов
(ОМНК)
ЗАДАНИЕ
N 5
сообщить
об ошибке
Тема:
Обобщенный метод наименьших квадратов
(ОМНК)
Начало формы




Конец формы
Для оценки параметров регрессионной модели с гетероскедастичными остатками используется _______ метод наименьших квадратов.
|
|
|
|
обобщенный |
|
|
|
|
традиционный |
|
|
|
|
двухшаговый |
|
|
|
|
косвенный |
![]() ЗАДАНИЕ
N 6
сообщить
об ошибке
Тема:
Оценка параметров линейных уравнений
регрессии
ЗАДАНИЕ
N 6
сообщить
об ошибке
Тема:
Оценка параметров линейных уравнений
регрессии
Начало формы




Конец формы
Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
|
|
|
|
линейной |
|
|
|
|
нелинейной |
|
|
|
|
экспоненциальной |
|
|
|
|
нормальной |
![]() ЗАДАНИЕ
N 7
сообщить
об ошибке
Тема:
Предпосылки МНК, методы их проверки
ЗАДАНИЕ
N 7
сообщить
об ошибке
Тема:
Предпосылки МНК, методы их проверки
Начало формы




Конец формы
Для
оценки
параметров эконометрической модели
линейного уравнения регрессии вида
![]() используется
метод наименьших квадратов (МНК), при
этом выдвигаются предпосылки относительно
величины …
используется
метод наименьших квадратов (МНК), при
этом выдвигаются предпосылки относительно
величины …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 8
сообщить
об ошибке
Тема:
Свойства оценок параметров эконометрической
модели, получаемых при помощи МНК
ЗАДАНИЕ
N 8
сообщить
об ошибке
Тема:
Свойства оценок параметров эконометрической
модели, получаемых при помощи МНК
Начало формы




Конец формы
Для регрессионной модели несмещенность оценки параметра означает, что математическое ожидание остатков равно …
|
|
|
|
0 |
|
|
|
|
оцениваемому параметру, рассчитанному по генеральной совокупности |
|
|
|
|
свободному члену уравнения регрессии |
|
|
|
|
1 |
![]() ЗАДАНИЕ
N 9
сообщить
об ошибке
Тема:
Линейное уравнение множественной
регрессии
ЗАДАНИЕ
N 9
сообщить
об ошибке
Тема:
Линейное уравнение множественной
регрессии
Начало формы




Конец формы
В
эконометрической модели линейного
уравнения множественной регрессии
![]() величина
параметра а
характеризует среднее по совокупности
значение зависимой переменной, при
значениях ___, равных 0.
величина
параметра а
характеризует среднее по совокупности
значение зависимой переменной, при
значениях ___, равных 0.
|
|
|
|
xj |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
a |
![]() ЗАДАНИЕ
N 10
сообщить
об ошибке
Тема:
Отбор факторов, включаемых в модель
множественной регрессии
ЗАДАНИЕ
N 10
сообщить
об ошибке
Тема:
Отбор факторов, включаемых в модель
множественной регрессии
Начало формы




Конец формы
Строится
эконометрическая модель уравнения
множественной регрессии для зависимости
y
от пяти факторов х(1),
х(2),
х(3),
х(4),
х(5).
Получена матрица парных коэффициентов
линейной корреляции (y
– зависимая переменная):
 Требование
отсутствия коллинеарных независимых
переменных выполняется в модели …
Требование
отсутствия коллинеарных независимых
переменных выполняется в модели …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 11
сообщить
об ошибке
Тема:
Спецификация эконометрической модели
ЗАДАНИЕ
N 11
сообщить
об ошибке
Тема:
Спецификация эконометрической модели
Начало формы




Конец формы
Особенность эконометрики как прикладной науки заключается в ____ существующих взаимосвязей социально-экономических показателей и систем.
|
|
|
|
количественном измерении |
|
|
|
|
качественном описании |
|
|
|
|
формулировании теорий |
|
|
|
|
схематическом описании |
![]() ЗАДАНИЕ
N 12
сообщить
об ошибке
Тема:
Фиктивные переменные
ЗАДАНИЕ
N 12
сообщить
об ошибке
Тема:
Фиктивные переменные
Начало формы




Конец формы
Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение …
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
–1 |
|
|
|
|
0,1 |
![]() ЗАДАНИЕ
N 13
сообщить
об ошибке
Тема:
Модели стационарных и нестационарных
временных рядов и их идентификация
ЗАДАНИЕ
N 13
сообщить
об ошибке
Тема:
Модели стационарных и нестационарных
временных рядов и их идентификация
Начало формы




Конец формы
Для стационарных временных рядов y1, у2, … yt, …, yn (t = 1, …, n) автоковариация зависит только от величины …
|
|
|
|
лага |
|
|
|
|
количества уровней ряда |
|
|
|
|
математического ожидания значений уровня ряда. |
|
|
|
|
начального значения процесса |
![]() ЗАДАНИЕ
N 14
сообщить
об ошибке
Тема:
Аддитивная и мультипликативная модели
временных рядов
ЗАДАНИЕ
N 14
сообщить
об ошибке
Тема:
Аддитивная и мультипликативная модели
временных рядов
Начало формы




Конец формы
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда не формируют следующие значения компонент уровня временного ряда …
|
|
|
|
yt = 7; T = -3,5; S = -2; E = -1 |
|
|
|
|
yt = 7; T = 7; S = 1; E = 1 |
|
|
|
|
yt = 7; T = 3,5; S = 2; E = 1 |
|
|
|
|
yt = 7; T = 3,5; S = -2; E = -1 |
![]() ЗАДАНИЕ
N 15
сообщить
об ошибке
Тема:
Временные ряды данных: характеристики
и общие понятия
ЗАДАНИЕ
N 15
сообщить
об ошибке
Тема:
Временные ряды данных: характеристики
и общие понятия
Начало формы




Конец формы
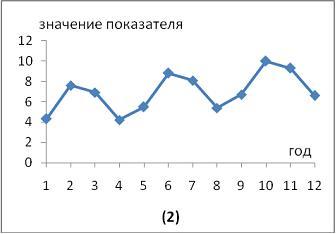
Изображенный
на рисунке временной ряд содержит
следующие компоненты:

|
|
|
|
убывающую тенденцию и случайную компоненту |
|
|
|
|
возрастающую тенденцию и случайную компоненту |
|
|
|
|
убывающую сезонную компоненту и случайную компоненту |
|
|
|
|
сезонную компоненту и убывающую случайную компоненту |
![]() ЗАДАНИЕ
N 16
сообщить
об ошибке
Тема:
Структура временного ряда
ЗАДАНИЕ
N 16
сообщить
об ошибке
Тема:
Структура временного ряда
Начало формы




Конец формы
Данная
таблица значений автокорреляционной
функции соответствует структуре
временного ряда …

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 17
сообщить
об ошибке
Тема:
Оценка качества нелинейных уравнений
регрессии
ЗАДАНИЕ N 17
сообщить
об ошибке
Тема:
Оценка качества нелинейных уравнений
регрессии
Начало формы




Конец формы
Для
нелинейного уравнения регрессии
рассчитано значение индекса детерминации
![]() .
Следовательно, доля объясненной дисперсии
в общей дисперсии зависимой переменной
для данного уравнения составляет …
.
Следовательно, доля объясненной дисперсии
в общей дисперсии зависимой переменной
для данного уравнения составляет …
|
|
|
|
0,6 |
|
|
|
|
0,6% |
|
|
|
|
0,4 |
|
|
|
|
0,4% |
Решение:
Уравнение
регрессии строится для моделирования
зависимой переменной. При этом общая
дисперсия зависимой переменной
принимается как целое, то есть за 1. Она
(1 – общая дисперсия) раскладывается на
две части: объясненная уравнением часть
и не объясненная уравнением (остаточная)
часть. Для каждой части рассчитывается
ее доля в общей дисперсии, то есть в 1.
Доля объясненной дисперсии в общей есть
не что иное как индекс детерминации
(для нелинейных уравнений) или коэффициент
детерминации (для линейных уравнений),
обозначается R2.
Доля остаточной дисперсии в общей
рассчитывается как разность (1–
R2).
Доля каждой из частей всегда не больше
1; доля есть часть, поэтому не имеет
единицы измерения. Можно рассчитать
также процент, тогда долю нужно умножить
на 100%, это значение будет показывать,
сколько процентов занимает та или иная
часть дисперсии (объясненная или
остаточная) в общей дисперсии, то есть
в 100%. В нашем случае
![]() ,
следовательно, доля объясненной дисперсии
зависимой переменной в ее общей дисперсии
составляет 0,6 (это правильный вариант
ответа); доля остаточной дисперсии
зависимой переменной в общей
составляет 0,4. В процентном соотношении
получаем: доля объясненной дисперсии
зависимой переменной в ее общей дисперсии
составляет 60%; доля остаточной дисперсии
зависимой переменной в общей
составляет 40%.
Поэтому правильный
вариант ответа «0,6».
,
следовательно, доля объясненной дисперсии
зависимой переменной в ее общей дисперсии
составляет 0,6 (это правильный вариант
ответа); доля остаточной дисперсии
зависимой переменной в общей
составляет 0,4. В процентном соотношении
получаем: доля объясненной дисперсии
зависимой переменной в ее общей дисперсии
составляет 60%; доля остаточной дисперсии
зависимой переменной в общей
составляет 40%.
Поэтому правильный
вариант ответа «0,6».
![]() ЗАДАНИЕ
N 18
сообщить
об ошибке
Тема:
Линеаризация нелинейных моделей
регрессии
ЗАДАНИЕ
N 18
сообщить
об ошибке
Тема:
Линеаризация нелинейных моделей
регрессии
Начало формы




Конец формы
При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется замена переменных. Указанным способом не может быть линеаризовано уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 19
сообщить
об ошибке
Тема:
Виды нелинейных уравнений регрессии
ЗАДАНИЕ N 19
сообщить
об ошибке
Тема:
Виды нелинейных уравнений регрессии