ЭКОНОМЕТРИКА 2

 ЗАДАНИЕ N 9 сообщить об ошибке Тема: Оценка качества подбора уравнения

Начало формы

Конец формы

Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации . Тогда долю остаточной дисперсии зависимой переменной характеризует величина …

 ЗАДАНИЕ N 10 сообщить об ошибке Тема: Оценка значимости параметров эконометрической модели

Начало формы

Конец формы

Если параметр эконометрической модели не является статистически значимым, то отвергается статистическая гипотеза о том, что его значение …

			отлично от 0
			равно 0
			равно 1
			равно коэффициенту парной корреляции

 ЗАДАНИЕ N 11 сообщить об ошибке Тема: Проверка статистической значимости эконометрической модели

Начало формы

Конец формы

Для совокупности из n единиц наблюдений построена модель линейного уравнения множественной регрессии с количеством параметров при независимых переменных, равным k. Тогда при расчете остаточной дисперсии на одну степень свободы величину дисперсии относят к значению …

			n – k  – 1
			n + k + 1
			n + k  – 1
			n + k

 ЗАДАНИЕ N 12 сообщить об ошибке Тема: Оценка тесноты связи

Начало формы

Конец формы

Для регрессионной модели вида  рассчитано значение коэффициента парной корреляции ; если , то связь между у и х …

			обратная
			прямая
			функциональная
			отсутствует

 ЗАДАНИЕ N 13 сообщить об ошибке Тема: Спецификация эконометрической модели

Начало формы

Конец формы

По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.

			линейные и нелинейные
			линейные и парные
			множественные и парные
			стохастические и вероятностные

 ЗАДАНИЕ N 14 сообщить об ошибке Тема: Отбор факторов, включаемых в модель множественной регрессии

Начало формы

Конец формы

Для эконометрической модели линейного уравнения множественной регрессии вида  построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х⁽¹⁾, х⁽²⁾, х⁽³⁾– независимые переменные): Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …

			x(1) и x(2)
			y и x(3)
			x(1)  и x(3)
			x(2) и x(3)

 ЗАДАНИЕ N 15 сообщить об ошибке Тема: Фиктивные переменные

Начало формы

Конец формы

Фиктивные переменные эконометрической модели …

			отражают качественные признаки исследуемого объекта наблюдения
			используются в случае неоднородных совокупностей данных
			отражают количественные признаки исследуемого объекта наблюдения
			используются в случае однородных совокупностей данных

  ЗАДАНИЕ N 16 сообщить об ошибке Тема: Линейное уравнение множественной регрессии

Начало формы

Конец формы

В эконометрической модели линейного уравнения регрессии  ошибкой модели является …

			a
			bj
			xj

Решение: Эконометрическая модель линейного уравнения регрессии имеет вид , где y – зависимая переменная, x_j – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, b_j – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является «».

 ЗАДАНИЕ N 17 сообщить об ошибке Тема: Классификация систем уравнений

Начало формы

Конец формы

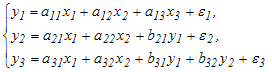Установите соответствие между видом и классом системы эконометрических уравнений; (1) (2) (3)

1			система взаимозависимых (одновременных) уравнений
2			система рекурсивных уравнений
3			система независимых уравнений
			система нормальных уравнений

 ЗАДАНИЕ N 18 сообщить об ошибке Тема: Общие понятия о системах уравнений, используемых в эконометрике

Начало формы

Конец формы

Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.

			двух
			трех
			одного
			бесконечно большого количества

 ЗАДАНИЕ N 19 сообщить об ошибке Тема: Идентификация систем эконометрических уравнений

Начало формы

Конец формы

Дана структурная форма модели системы одновременных уравнений: Установите соответствие между обозначением и его наименованием: (1) (2) (3)

1			структурный коэффициент
2			ошибка уравнения системы
3			эндогенная переменная
			приведенный коэффициент

 ЗАДАНИЕ N 20 сообщить об ошибке Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)

Начало формы

Конец формы

Определите последовательность этапов алгоритма обычного метода наименьших квадратов (МНК) для оценки параметров системы независимых уравнений.

1			разложение системы независимых уравнений на отдельные (изолированные) уравнения регрессии, число которых определяется количеством эндогенных переменных модели
2			построение системы нормальных уравнений для каждого отдельного (изолированного) уравнения
3			расчет оценок параметров каждого отдельного (изолированного) уравнения
4			запись системы независимых уравнений с найденными значениями оценок параметров

 ЗАДАНИЕ N 21 сообщить об ошибке Тема: Аддитивная и мультипликативная модели временных рядов

Начало формы

Конец формы

Для временного ряда, отображенного на рисунке одним из методов построения модели ряда является выравнивание ряда по методу скользящей средней. При этом количество слагаемых при расчете значений выровненного ряда будет равно …

			4
			2
			20
			5

  ЗАДАНИЕ N 22 сообщить об ошибке Тема: Модели стационарных и нестационарных временных рядов и их идентификация

Начало формы

Конец формы

Рассмотрим стационарный временной ряд y₁, у₂, … y_t, …, y_n, для которого математическое ожидание E(y_t) = 0 (где t = 1, …, n). Тогда данный стационарный ряд является реализацией процесса «____ шум».

			белый
			серый
			нормальный
			стандартизованный

Решение: Процесс «белый шум» является частным случаем стационарного временного ряда, для которого математическое ожидание значений уровня этого ряда равно 0 (одно из определений процесса «белый шум»). Правильный вариант ответа – «белый».

 ЗАДАНИЕ N 23 сообщить об ошибке Тема: Временные ряды данных: характеристики и общие понятия

Начало формы

Конец формы

Изображенный на рисунке временной ряд содержит случайную …

			компоненту
			сезонную компоненту
			циклическую компоненту
			тенденцию

 ЗАДАНИЕ N 24 сообщить об ошибке Тема: Структура временного ряда

Начало формы

Конец формы

Вывод о присутствии в данном временном ряде сезонной компоненты можно сделать по значению коэффициента автокорреляции ____ порядка.  

			четвертого
			первого
			второго
			восьмого

Образовательное учреждение: Мордовский государственный университет им. Н.П. Огарева Специальность: 080105.65 - Финансы и кредит Группа: 308 экон Дисциплина: Эконометрика Идентификатор студента: Качанова Юлия Александровна Логин: 03fs482666 Начало тестирования: 2012-12-03 18:14:38 Завершение тестирования: 2012-12-03 18:29:13 Продолжительность тестирования: 14 мин. Заданий в тесте: 24 Кол-во правильно выполненных заданий: 19 Процент правильно выполненных заданий: 79 %

 ЗАДАНИЕ N 1 сообщить об ошибке Тема: Проверка статистической значимости эконометрической модели

Начало формы

Конец формы

Проверку статистической значимости построенной эконометрической модели на основе F-критерия осуществляют с использованием …

			статистических гипотез
			стандартизованных переменных
			системы нормальных уравнений
			коллективных гипотез

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Оценка качества подбора уравнения

Начало формы

Конец формы

Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации  (см. рис.). На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.

			83,1 %
			16,9 %
			0,831 %
			0,169 %

Решение: Значение коэффициента детерминации  характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, что в нашем случае составляет 0,831. В процентном соотношении эта величина равна . Поэтому верный вариант ответа – «83,1%».