ЭКОНОМЕТРИКА 2

			n – 1
			n + 1
			n
			n / 2

  ЗАДАНИЕ N 20 сообщить об ошибке Тема: Оценка тесноты связи

Начало формы

Конец формы

Для регрессионной модели вида  знак при значении коэффициента парной корреляции , рассчитанного для этого уравнения, совпадает со знаком при …

			b
			x
			a

Решение: Значение коэффициента парной корреляции  характеризует тесноту связи между зависимой переменной  и независимой переменной . Его знак показывает характер связи между переменными  и  . Если , то при увеличении у переменная х увеличивается, а при уменьшении у переменная х уменьшается; связь между переменными  и  прямая. Если , то при увеличении у переменная х уменьшается, а при уменьшении у переменная х  увеличивается; связь между переменными  и  обратная. Если линейную модель парной регрессии записать в виде  , то знак при коэффициенте b при переменной  будет также свидетельствовать о характере связи. Если , то при увеличении у переменная х увеличивается, а при уменьшении у переменная х уменьшается; связь между переменными  и  прямая. Если , то при увеличении у переменная х уменьшается, а при уменьшении у переменная х увеличивается; что связь между переменными  и  обратная. Таким образом, знак при  совпадает со знаком при b, что и является правильным вариантом ответа.

 ЗАДАНИЕ N 21 сообщить об ошибке Тема: Классификация систем уравнений

Начало формы

Конец формы

Установите соответствие между видом и классом системы эконометрических уравнений: (1)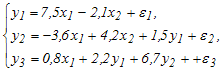 (2)

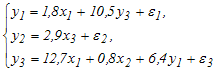
1			система рекурсивных уравнений
2			система взаимозависимых (одновременных) уравнений
			система независимых уравнений

  ЗАДАНИЕ N 22 сообщить об ошибке Тема: Общие понятия о системах уравнений, используемых в эконометрике

Начало формы

Конец формы

Необходимость использования систем эконометрических уравнений вызвана …

			невозможностью адекватного описания экономических процессов только на основе одного уравнения
			необходимостью учета всех существенных взаимосвязей внутри социально-экономической системы
			отсутствием взаимосвязей между независимыми переменными регрессионной модели
			более высоким качеством отдельного уравнения регрессии по сравнению с системой эконометрических уравнений

Решение: Рассмотрим все предложенные варианты ответов и сопоставим их с необходимостью использования систем эконометрических уравнений. Вариант «отсутствием взаимосвязей между независимыми переменными регрессионной модели» при такой ситуации можно рекомендовать использовать уравнение множественной регрессии, а не систему уравнений (этот вариант ответа неверный). Вариант «более высоким качеством отдельного уравнения регрессии по сравнению с системой эконометрических уравнений» опровергает необходимость использования систем эконометрических уравнений, потому что, как правило, использование системы уравнений для описания этого же экономического явления или процесса дает более высокие результаты моделирования, т.к. позволяет учесть реальное взаимодействие элементов социально-экономической системы (этот вариант ответа неверный). Вариант «невозможностью адекватного описания экономических процессов только на основе одного уравнения» отражает одно из условий необходимости использования систем уравнений (этот вариант ответа правильный). Вариант «необходимостью учесть все существенные взаимосвязи внутри социально-экономической системы» отражает одно из условий необходимости использования систем уравнений (этот вариант ответа правильный).

 ЗАДАНИЕ N 23 сообщить об ошибке Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)

Начало формы

Конец формы

Определите последовательность этапов алгоритма оценки параметров модели системы эконометрических уравнений.

1			определение класса системы эконометрических уравнений
2			оценка возможности идентификации модели
3			выбор метода оценки параметров модели в соответствии с идентифицируемостью модели
4			расчет оценок параметров модели системы эконометрических уравнений

  ЗАДАНИЕ N 24 сообщить об ошибке Тема: Идентификация систем эконометрических уравнений

Начало формы

Конец формы

Установите соответствие между формой модели системы одновременных (совместных) эконометрических уравнений и видом системы. (1) приведенная форма модели (2) структурная форма модели

1
2

Решение: Рассмотрим каждую из систем эконометрических уравнений. Структурная форма модели отражает структуру связей между переменными, в правой части каждого уравнения структурной формой модели стоят независимые переменные х и зависимые переменные y других уравнений. Структурной форме модели соответствует система Приведенная форма модели представляет собой систему независимых уравнений, в правой части уравнений стоят только независимые переменные с приведенными коэффициентами . Приведенной форме модели соответствует система Вариант ответа , предложенный в ответе, содержит ошибку, так как в правой части всех уравнений системы стоит переменная у₁. Поэтому данная система не может быть отнесена ни к приведенной, ни к структурной форме модели, это неправильный вариант ответа.

Образовательное учреждение: Мордовский государственный университет им. Н.П. Огарева Специальность: 080105.65 - Финансы и кредит Группа: 308 экон Дисциплина: Эконометрика Идентификатор студента: Названова Юлия Сергеевна Логин: 03fs482676 Начало тестирования: 2012-12-03 16:57:28 Завершение тестирования: 2012-12-03 17:36:53 Продолжительность тестирования: 39 мин. Заданий в тесте: 24 Кол-во правильно выполненных заданий: 18 Процент правильно выполненных заданий: 75 %

  ЗАДАНИЕ N 1 сообщить об ошибке Тема: Оценка качества нелинейных уравнений регрессии

Начало формы

Конец формы

Для нелинейной регрессионной модели зависимости рассчитано значение индекса детерминации R² = 0,9. Тогда значение индекса корреляции составит …

Решение: Значение индекса детерминации R² и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением . Следовательно, значение индекса корреляции составит .

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Виды нелинейных уравнений регрессии

Начало формы

Конец формы

Не является полиномом регрессионная модель …

Решение: Одним из видов нелинейных зависимостей в эконометрике являются полиномиальные зависимости в виде функции вида , где j = 1…k,  k  – степень полинома (k – целое неотрицательное число). Так, полином первой степени имеет вид  (линейная функция – частный вид полинома первой степени), полином второй степени – , третьей степени –  и т.д. до полинома степени k. Из предложенных вариантов ответа полиномом не является модель вида . Это правильный вариант ответа.

 ЗАДАНИЕ N 3 сообщить об ошибке Тема: Линеаризация нелинейных моделей регрессии

Начало формы

Конец формы

При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной  . Указанным способом может быть линеаризовано уравнение …

  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Нелинейные зависимости в экономике

Начало формы

Конец формы

Нелинейным уравнением множественной регрессии является …

Решение: Рассмотрим каждую из моделей:  – линейное уравнение множественной регрессии;  – линейное уравнение парной регрессии, которое можно переписать в виде ;  – нелинейное уравнение парной регрессии;  – нелинейное уравнение множественной регрессии – модель, которая является правильным вариантом ответа. Остальные модели не подходят под спецификацию уравнения регрессии, заданную в постановке вопроса, поэтому не являются правильными вариантами ответов.

 ЗАДАНИЕ N 5 сообщить об ошибке Тема: Классификация систем уравнений

Начало формы

Конец формы

Установите соответствие между классом и видом системы эконометрических уравнений: (1) система взаимозависимых (одновременных) уравнений (2) система независимых уравнений

1
2

 ЗАДАНИЕ N 6 сообщить об ошибке Тема: Идентификация систем эконометрических уравнений

Начало формы

Конец формы

Установите соответствие между видом системы одновременных (совместных) эконометрических уравнений и формой модели: (1) (2)

1			структурная форма модели
2			приведенная форма модели
			форма нормальных уравнений

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Общие понятия о системах уравнений, используемых в эконометрике

Начало формы

Конец формы

Необходимость использования систем эконометрических уравнений вызвана …

			невозможностью адекватного описания экономических процессов только на основе одного уравнения
			необходимостью учета всех существенных взаимосвязей внутри социально-экономической системы
			отсутствием взаимосвязей между независимыми переменными регрессионной модели
			более высоким качеством отдельного уравнения регрессии по сравнению с системой эконометрических уравнений

Решение: Рассмотрим все предложенные варианты ответов и сопоставим их с необходимостью использования систем эконометрических уравнений. Вариант «отсутствием взаимосвязей между независимыми переменными регрессионной модели» при такой ситуации можно рекомендовать использовать уравнение множественной регрессии, а не систему уравнений (этот вариант ответа неверный). Вариант «более высоким качеством отдельного уравнения регрессии по сравнению с системой эконометрических уравнений» опровергает необходимость использования систем эконометрических уравнений, потому что, как правило, использование системы уравнений для описания этого же экономического явления или процесса дает более высокие результаты моделирования, т.к. позволяет учесть реальное взаимодействие элементов социально-экономической системы (этот вариант ответа неверный). Вариант «невозможностью адекватного описания экономических процессов только на основе одного уравнения» отражает одно из условий необходимости использования систем уравнений (этот вариант ответа правильный). Вариант «необходимостью учесть все существенные взаимосвязи внутри социально-экономической системы» отражает одно из условий необходимости использования систем уравнений (этот вариант ответа правильный).

 ЗАДАНИЕ N 8 сообщить об ошибке Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)

Начало формы