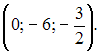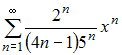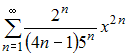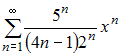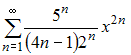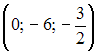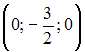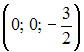Вариант 2
.docx
![]() ЗАДАНИЕ
N 35
отправить
сообщение разработчикам
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии Y
на X
имеет вид
ЗАДАНИЕ
N 35
отправить
сообщение разработчикам
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии Y
на X
имеет вид
![]() а
выборочные средние квадратические
отклонения равны:
а
выборочные средние квадратические
отклонения равны:
![]() Тогда
выборочный коэффициент корреляции
Тогда
выборочный коэффициент корреляции
![]() равен …
равен …
|
|
|
|
0,15 |
|
|
|
|
–2,4 |
|
|
|
|
2,4 |
|
|
|
|
–0,15 |
![]() ЗАДАНИЕ
N 36
отправить
сообщение разработчикам
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема n = 81:
ЗАДАНИЕ
N 36
отправить
сообщение разработчикам
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема n = 81:
 Тогда
значение n3
равно …
Тогда
значение n3
равно …
|
|
|
|
34 |
|
|
|
|
81 |
|
|
|
|
47 |
|
|
|
|
33 |
![]() ЗАДАНИЕ N 37
отправить
сообщение разработчикам
Тема:
Интервальные оценки параметров
распределения
Точечная
оценка среднего квадратического
отклонения нормально распределенного
количественного признака равна 3,5. Тогда
его интервальная оценка может иметь
вид …
ЗАДАНИЕ N 37
отправить
сообщение разработчикам
Тема:
Интервальные оценки параметров
распределения
Точечная
оценка среднего квадратического
отклонения нормально распределенного
количественного признака равна 3,5. Тогда
его интервальная оценка может иметь
вид …
|
|
|
|
(0; 8,33) |
|
|
|
|
(3,5; 8,33) |
|
|
|
|
(0; 3,5) |
|
|
|
|
(–1,33; 8,33) |
Решение:
Интервальной
оценкой среднего квадратического
отклонения
![]() нормально
распределенного количественного
признака служит доверительный
интервал
нормально
распределенного количественного
признака служит доверительный
интервал
![]() при
при
![]() или
или
![]() при
при
![]() где
q
находят по соответствующей таблице
приложений.
Этому определению
удовлетворяет интервал
где
q
находят по соответствующей таблице
приложений.
Этому определению
удовлетворяет интервал
![]()
![]() ЗАДАНИЕ N 38
отправить
сообщение разработчикам
Тема:
Область сходимости степенного ряда
Радиус
сходимости равен 2,5 для степенного
ряда …
ЗАДАНИЕ N 38
отправить
сообщение разработчикам
Тема:
Область сходимости степенного ряда
Радиус
сходимости равен 2,5 для степенного
ряда …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Радиус
сходимости равен 2,5 для степенного ряда
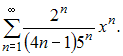 Действительно,
Действительно,
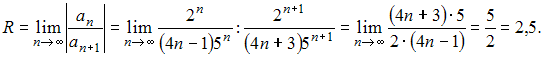
![]() ЗАДАНИЕ
N 39
отправить
сообщение разработчикам
Тема:
Числовые последовательности
Предел
числовой последовательности
ЗАДАНИЕ
N 39
отправить
сообщение разработчикам
Тема:
Числовые последовательности
Предел
числовой последовательности
![]() …
…
|
|
|
|
не существует |
|
|
|
|
равен – 0,75 |
|
|
|
|
равен
|
|
|
|
|
равен 0 |
![]() ЗАДАНИЕ
N 40
отправить
сообщение разработчикам
Тема:
Сходимость числовых рядов
Даны
числовые ряды:
А)
ЗАДАНИЕ
N 40
отправить
сообщение разработчикам
Тема:
Сходимость числовых рядов
Даны
числовые ряды:
А)
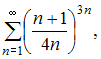 В)
В)
 Тогда …
Тогда …
|
|
|
|
ряд А) сходится, ряд В) расходится |
|
|
|
|
ряд А) расходится, ряд В) расходится |
|
|
|
|
ряд А) сходится, ряд В) сходится |
|
|
|
|
ряд А) расходится, ряд В) сходится |
![]() ЗАДАНИЕ N 41
отправить
сообщение разработчикам
Тема:
Плоскость в пространстве
Плоскость
проходит через точку
ЗАДАНИЕ N 41
отправить
сообщение разработчикам
Тема:
Плоскость в пространстве
Плоскость
проходит через точку
![]() и
отсекает на осях абсцисс и ординат в
положительных направлениях отрезки
длины 3 и 5 соответственно. Тогда общее
уравнение плоскости имеет вид …
и
отсекает на осях абсцисс и ординат в
положительных направлениях отрезки
длины 3 и 5 соответственно. Тогда общее
уравнение плоскости имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости «в отрезках» имеет вид
![]() где
где
![]() –
длины отрезков, отсекаемых плоскостью
на осях Ox,
Oy
и Oz
соответственно. Подставим в это уравнение
значения
–
длины отрезков, отсекаемых плоскостью
на осях Ox,
Oy
и Oz
соответственно. Подставим в это уравнение
значения
![]()
![]() и
координаты точки
и
координаты точки
![]()
![]() Тогда
Тогда
![]() и
общее уравнение плоскости примет вид
и
общее уравнение плоскости примет вид
![]()
![]() ЗАДАНИЕ
N 42
отправить
сообщение разработчикам
Тема:
Прямоугольные координаты на плоскости
В
треугольнике с вершинами
ЗАДАНИЕ
N 42
отправить
сообщение разработчикам
Тема:
Прямоугольные координаты на плоскости
В
треугольнике с вершинами
![]()
![]() и
и
![]() проведена
медиана AM,
длина которой равна …
проведена
медиана AM,
длина которой равна …
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
![]() ЗАДАНИЕ
N 43
отправить
сообщение разработчикам
Тема:
Прямая на плоскости
Уравнение
геометрического места точек, равноудаленных
от двух данных точек
ЗАДАНИЕ
N 43
отправить
сообщение разработчикам
Тема:
Прямая на плоскости
Уравнение
геометрического места точек, равноудаленных
от двух данных точек
![]() и
и
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 44
отправить
сообщение разработчикам
Тема:
Поверхности второго порядка
Координаты
вершины линии пересечения плоскости
ЗАДАНИЕ N 44
отправить
сообщение разработчикам
Тема:
Поверхности второго порядка
Координаты
вершины линии пересечения плоскости
![]() и
поверхности
и
поверхности
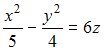 равны …
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
линии пересечения плоскости
![]() и
поверхности
и
поверхности
 получим
из решения системы
получим
из решения системы
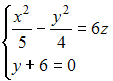 .
То есть
.
То есть
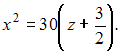 Это
уравнение параболы. Тогда координаты
вершины параболы будут равны
Это
уравнение параболы. Тогда координаты
вершины параболы будут равны