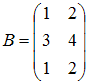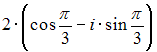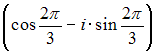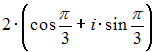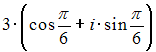Вариант 2
.docx
![]() ЗАДАНИЕ
N 1
отправить
сообщение разработчикам
Тема:
Дифференциальное исчисление
ФНП
Приближенное
значение функции
ЗАДАНИЕ
N 1
отправить
сообщение разработчикам
Тема:
Дифференциальное исчисление
ФНП
Приближенное
значение функции
![]() в
точке
в
точке
![]() вычисленное
с помощью полного дифференциала, равно …
вычисленное
с помощью полного дифференциала, равно …
|
|
|
|
5,002 |
|
|
|
|
5,02 |
|
|
|
|
5,062 |
|
|
|
|
5,001 |
![]() ЗАДАНИЕ N 2
отправить
сообщение разработчикам
Тема:
Основные методы интегрирования
Множество
первообразных функции
ЗАДАНИЕ N 2
отправить
сообщение разработчикам
Тема:
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции методом интегрирования
по частям по формуле
![]() Тогда
Тогда
![]()
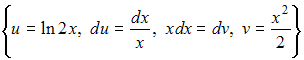
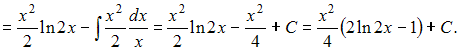
![]() ЗАДАНИЕ N 3
отправить
сообщение разработчикам
Тема:
Непрерывность функции, точки разрыва
Для
функции
ЗАДАНИЕ N 3
отправить
сообщение разработчикам
Тема:
Непрерывность функции, точки разрыва
Для
функции
![]() точка
точка
![]() является
точкой …
является
точкой …
|
|
|
|
разрыва второго рода |
|
|
|
|
разрыва первого рода |
|
|
|
|
непрерывности |
|
|
|
|
устранимого разрыва |
Решение:
Вычислим
односторонние пределы функции
![]() в
точке
в
точке
![]()
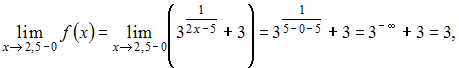
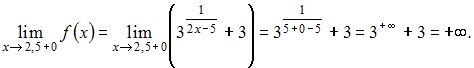 Так
как один из односторонних пределов в
точке
Так
как один из односторонних пределов в
точке
![]() а
именно
а
именно
![]() то
точка
то
точка
![]() является
точкой разрыва второго рода.
является
точкой разрыва второго рода.
![]() ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Длина
дуги кривой
ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Длина
дуги кривой
![]() от
точки
от
точки
![]() до
точки
до
точки
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 5
отправить
сообщение разработчикам
Тема:
Интерполирование функций: интерполяционные
полиномы Лагранжа
Функция
ЗАДАНИЕ
N 5
отправить
сообщение разработчикам
Тема:
Интерполирование функций: интерполяционные
полиномы Лагранжа
Функция
![]() представлена
таблицей
представлена
таблицей
 Тогда
значение
Тогда
значение
![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– 6 |
![]() ЗАДАНИЕ N 6
отправить
сообщение разработчикам
Тема:
Численные методы решения дифференциальных
уравнений и систем
Методом
Эйлера с шагом
ЗАДАНИЕ N 6
отправить
сообщение разработчикам
Тема:
Численные методы решения дифференциальных
уравнений и систем
Методом
Эйлера с шагом
![]() решается
задача Коши для системы дифференциальных
уравнений
решается
задача Коши для системы дифференциальных
уравнений
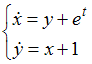 с
начальными условиями
с
начальными условиями
![]()
![]() Тогда
значения искомых функций
Тогда
значения искомых функций
![]() и
и
![]() равны …
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Алгоритм
Эйлера решения задачи Коши для системы
дифференциальных уравнений:
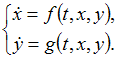
![]()
![]() реализуется
по формулам:
реализуется
по формулам:
![]()
![]()
![]()
![]() где
h
– шаг метода,
где
h
– шаг метода,
![]()
![]() а
а
![]() и
и
![]() –
искомые функции задачи Коши.
В
рассматриваемой задаче требуется
выполнить только один шаг метода
Эйлера.
В нашем случае
–
искомые функции задачи Коши.
В
рассматриваемой задаче требуется
выполнить только один шаг метода
Эйлера.
В нашем случае
![]()
![]()
![]()
![]()
![]()
![]() Тогда
Тогда
![]()
![]()
![]() ЗАДАНИЕ N 7
отправить
сообщение разработчикам
Тема:
Численное дифференцирование и
интегрирование
Значение
определенного интеграла
ЗАДАНИЕ N 7
отправить
сообщение разработчикам
Тема:
Численное дифференцирование и
интегрирование
Значение
определенного интеграла
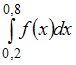 по
формуле прямоугольников можно приближенно
найти как …
по
формуле прямоугольников можно приближенно
найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Воспользуемся,
например, формулой «левых» прямоугольников
приближенного вычисления определенного
интеграла:
 где
где
![]() Пусть
Пусть
![]() Тогда
Тогда
![]()
![]()
![]() Следовательно,
Следовательно,
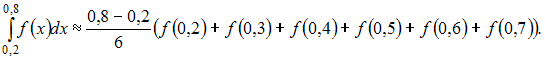
![]() ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Умножение матриц
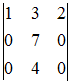
Умножение
матрицы A
на матрицу B
возможно, если эти матрицы имеют
вид …
ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Умножение матриц
Умножение
матрицы A
на матрицу B
возможно, если эти матрицы имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 9
отправить
сообщение разработчикам
Тема:
Базис и размерность линейного
пространства
Линейно
зависимыми будут вектора …
ЗАДАНИЕ
N 9
отправить
сообщение разработчикам
Тема:
Базис и размерность линейного
пространства
Линейно
зависимыми будут вектора …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 10
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений
Система
ЗАДАНИЕ N 10
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений
Система
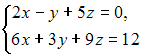 будет …
будет …
|
|
|
|
совместной и неопределенной |
|
|
|
|
несовместной и неопределенной |
|
|
|
|
совместной и определенной |
|
|
|
|
несовместной и определенной |
Решение:
По
методу Гаусса приведем матрицу системы
с помощью элементарных преобразований
строк к трапецеидальной или треугольной
форме. Запишем расширенную матрицу
системы и преобразуем ее:
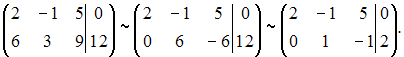 Значит,
ранг расширенной матрицы равен рангу
основной матрицы и система будет
совместной. Так как количество переменных
больше ранга матрицы, система имеет
бесконечное число решений, а значит,
является неопределенной.
Значит,
ранг расширенной матрицы равен рангу
основной матрицы и система будет
совместной. Так как количество переменных
больше ранга матрицы, система имеет
бесконечное число решений, а значит,
является неопределенной.
![]() ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Вычисление определителей
Определитель
не
равный
нулю может иметь вид …
ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Вычисление определителей
Определитель
не
равный
нулю может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 12
отправить
сообщение разработчикам
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции
ЗАДАНИЕ
N 12
отправить
сообщение разработчикам
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции
![]() в
точке
в
точке
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 13
отправить
сообщение разработчикам
Тема:
Комплексные числа и их представление
Комплексное
число задано в показательной форме
ЗАДАНИЕ N 13
отправить
сообщение разработчикам
Тема:
Комплексные числа и их представление
Комплексное
число задано в показательной форме
![]() Тогда
тригонометрическая форма записи
сопряженного к нему числа
Тогда
тригонометрическая форма записи
сопряженного к нему числа
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Показательная
форма комплексного числа имеет вид:
![]() а
тригонометрическая –
а
тригонометрическая –
![]() Так
как
Так
как
![]() а
главное значение аргумента
а
главное значение аргумента
![]() то
то
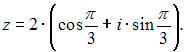 Если
Если
![]() то
то
![]() В
нашем случае
В
нашем случае
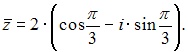
![]() ЗАДАНИЕ N 14
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Решение
системы уравнений
ЗАДАНИЕ N 14
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Решение
системы уравнений
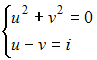 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выразим
![]() из
второго уравнения
из
второго уравнения
![]() и
подставим в первое уравнение системы
и
подставим в первое уравнение системы
![]() Получим
квадратное уравнение
Получим
квадратное уравнение
![]() Его
решения
Его
решения
![]()
![]() Соответствующие
им значения переменной
Соответствующие
им значения переменной
![]() будут
равны
будут
равны
![]()
![]() Таким
образом, решения системы будут иметь
вид:
Таким
образом, решения системы будут иметь
вид:
![]()
![]() и
и
![]()
![]()
![]() ЗАДАНИЕ N 15
отправить
сообщение разработчикам
Тема:
Типы дифференциальных уравнений
Уравнение
ЗАДАНИЕ N 15
отправить
сообщение разработчикам
Тема:
Типы дифференциальных уравнений
Уравнение
![]() является …
является …
|
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
|
|
|
|
однородным относительно x и y дифференциальным уравнением первого порядка |
|
|
|
|
уравнением Бернулли |
|
|
|
|
дифференциальным уравнением с разделяющимися переменными |
Решение:
Уравнение
![]() может
быть сведено к уравнению вида
может
быть сведено к уравнению вида
![]() Действительно,
Действительно,
![]() поэтому
данное уравнение является дифференциальным
линейным уравнением первого порядка.
поэтому
данное уравнение является дифференциальным
линейным уравнением первого порядка.
![]() ЗАДАНИЕ
N 16
отправить
сообщение разработчикам
Тема:
Однородные дифференциальные уравнения
Общее
решение дифференциального уравнения
ЗАДАНИЕ
N 16
отправить
сообщение разработчикам
Тема:
Однородные дифференциальные уравнения
Общее
решение дифференциального уравнения
![]() имеет
вид …
имеет
вид …






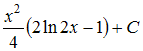

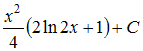


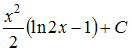

















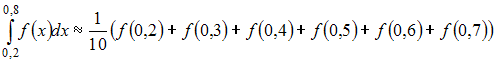

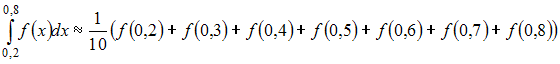

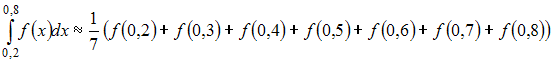

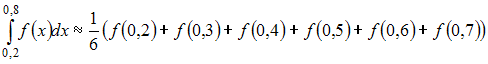

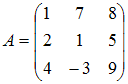 и
и
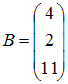

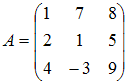 и
и

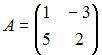 и
и

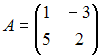 и
и