Вариант 1
.docx
ЗАДАНИЕ N 41
отправить
сообщение разработчикам
Тема:
Векторное произведение векторов
Даны
два вектора:
и
Тогда
вектор
будет
перпендикулярен и вектору
и
вектору
при
равном …
|
|
|
|
4 |
|
|
|
|
– 2 |
|
|
|
|
– 4 |
|
|
|
|
|
Решение:
Вектор
,
перпендикулярный и вектору
и
вектору
можно
найти как результат векторного
произведения векторов
и
заданных
своими координатами:
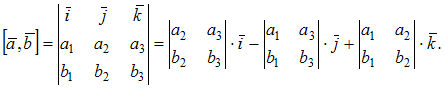В
нашем случае
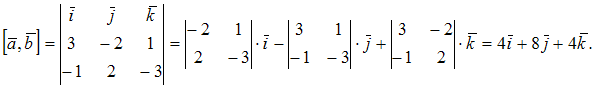Вектора
и
должны
быть коллинеарны. То есть
и,
следовательно
ЗАДАНИЕ
N 42
отправить
сообщение разработчикам
Тема:
Комплексные числа и их представление
Показательная
форма записи комплексного числа
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 43
отправить
сообщение разработчикам
Тема:
Дифференцирование функции комплексного
переменного
Если
то
равно …
|
|
|
|
4 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 44
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Если
и
являются
решением системы линейных уравнений
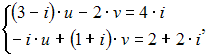то
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
Решение:
Решим
систему методом Крамера. Для этого
вычислим определитель системы:
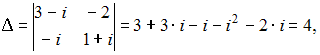и
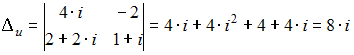вспомогательные определители:
и
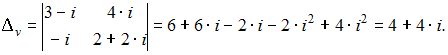Тогда
по формулам Крамера получим:
и
Следовательно,
