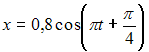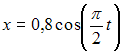Вариант 3

  ЗАДАНИЕ N 37 отправить сообщение разработчикам Тема: Плоскость в пространстве Геометрическое место точек, удаленных от плоскости  на 2 единицы, может иметь вид …

Решение: Расстояние от точки  до плоскости  находится по формуле 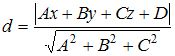 или 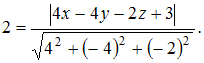Тогда  Отсюда можно получить общее уравнение плоскости, например, в виде

 ЗАДАНИЕ N 38 отправить сообщение разработчикам Тема: Прямая на плоскости Прямая задана в параметрическом виде 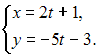Тогда ее общее уравнение имеет вид …

  ЗАДАНИЕ N 39 отправить сообщение разработчикам Тема: Прямоугольные координаты на плоскости Даны точки  и  Тогда координаты точки  симметричной точке B относительно точки  A, равны …

Решение: Воспользуемся формулой деления отрезка пополам. Координаты точки  делящей отрезок между точками  и  пополам, находятся по формулам   Тогда координаты точки  находятся как   то есть точка  имеет координаты

  ЗАДАНИЕ N 40 отправить сообщение разработчикам Тема: Поверхности второго порядка Уравнение геометрического места точек, равноудаленных от точки  и от плоскости  имеет вид …

Решение: Пусть точка  удовлетворяет заданным условиям. Расстояние от точки  A до точки M  определяется из соотношения  а до плоскости  как 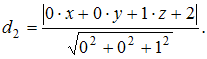Так как точка  равноудалена от точки  и плоскости  то  то есть Тогда   или

 ЗАДАНИЕ N 41 отправить сообщение разработчикам Тема: Элементы гармонического анализа Функцией, ортогональной к функции  на 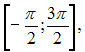  не является …

  ЗАДАНИЕ N 42 отправить сообщение разработчикам Тема: Периодические функции Период функции  равен …

Решение: Если – периодическая функция с периодом  то какова бы ни была функция F, сложная функция – также функция периодическая, причем число T является и ее периодом. Функция  имеет период  Следовательно, исходная функция имеет тот же период

  ЗАДАНИЕ N 43 отправить сообщение разработчикам Тема: Гармонические колебания Гармонические колебания с частотой 0,5 амплитудой колебания   и начальной фазой, равной нулю, описывается уравнением …

Решение: Уравнение гармонических колебаний имеет вид 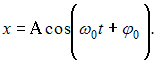 Тогда, так как    то получим

  ЗАДАНИЕ N 44 отправить сообщение разработчикам Тема: Ряд Фурье. Теорема Дирихле Значение ряда Фурье функции 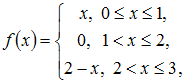  в точке  равно …

			1
			0

Решение: Значение ряда Фурье в точке конечного разрыва x₀ вычисляется по формуле   тогда