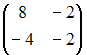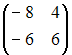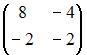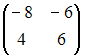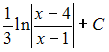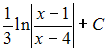Вариант 3
.docx![]() ЗАДАНИЕ
N 1
отправить
сообщение разработчикам
Тема:
Градиент скалярного поля
Модуль
градиента скалярного поля
ЗАДАНИЕ
N 1
отправить
сообщение разработчикам
Тема:
Градиент скалярного поля
Модуль
градиента скалярного поля
![]() в
точке пересечения оси Oz
с поверхностью
в
точке пересечения оси Oz
с поверхностью
![]() равен …
равен …
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
![]() ЗАДАНИЕ N 2
отправить
сообщение разработчикам
Тема:
Векторное произведение векторов
Векторное
произведение векторов
ЗАДАНИЕ N 2
отправить
сообщение разработчикам
Тема:
Векторное произведение векторов
Векторное
произведение векторов
![]() и
и
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
![]() Так
как
Так
как
![]()
![]()
![]() то
то
![]() Векторное
произведение ортов
Векторное
произведение ортов
![]() Следовательно
Следовательно
![]()
![]() ЗАДАНИЕ
N 3
отправить
сообщение разработчикам
Тема:
Норма вектора в евклидовом пространстве
В
евклидовом пространстве со стандартным
скалярным произведением норма вектора
ЗАДАНИЕ
N 3
отправить
сообщение разработчикам
Тема:
Норма вектора в евклидовом пространстве
В
евклидовом пространстве со стандартным
скалярным произведением норма вектора
![]() равна
2, норма вектора
равна
2, норма вектора
![]() равна
3, их скалярное произведение равно 2.
Тогда норма вектора
равна
3, их скалярное произведение равно 2.
Тогда норма вектора
![]() равна …
равна …
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
9 |
|
|
|
|
–1 |
![]() ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Интервальные оценки параметров
распределения
Построен
доверительный интервал для оценки
математического ожидания нормально
распределенного количественного
признака при известном
среднем квадратическом отклонении
генеральной совокупности. Тогда при
уменьшении объема выборки в два раза
значение точности этой оценки …
ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Интервальные оценки параметров
распределения
Построен
доверительный интервал для оценки
математического ожидания нормально
распределенного количественного
признака при известном
среднем квадратическом отклонении
генеральной совокупности. Тогда при
уменьшении объема выборки в два раза
значение точности этой оценки …
|
|
|
|
увеличится
в
|
|
|
|
|
уменьшится в два раза |
|
|
|
|
увеличится в два раза |
|
|
|
|
уменьшится
в
|
![]() ЗАДАНИЕ
N 5
отправить
сообщение разработчикам
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
ЗАДАНИЕ
N 5
отправить
сообщение разработчикам
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
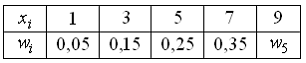 Тогда
частота варианты
Тогда
частота варианты
![]() в
выборке равна …
в
выборке равна …
|
|
|
|
28 |
|
|
|
|
63 |
|
|
|
|
42 |
|
|
|
|
35 |
![]() ЗАДАНИЕ
N 6
отправить
сообщение разработчикам
Тема:
Элементы корреляционного анализа
При
построении выборочного уравнения парной
регрессии вычислены выборочный
коэффициент корреляции
ЗАДАНИЕ
N 6
отправить
сообщение разработчикам
Тема:
Элементы корреляционного анализа
При
построении выборочного уравнения парной
регрессии вычислены выборочный
коэффициент корреляции
![]() и
выборочные средние квадратические
отклонения
и
выборочные средние квадратические
отклонения
![]() Тогда
выборочный коэффициент регрессии Y
на X
равен …
Тогда
выборочный коэффициент регрессии Y
на X
равен …
|
|
|
|
1,08 |
|
|
|
|
–1,08 |
|
|
|
|
0,27 |
|
|
|
|
–0,27 |
![]() ЗАДАНИЕ N 7
отправить
сообщение разработчикам
Тема:
Точечные оценки параметров распределения
Если
все варианты
ЗАДАНИЕ N 7
отправить
сообщение разработчикам
Тема:
Точечные оценки параметров распределения
Если
все варианты
![]() исходного
вариационного ряда увеличить на девять
единиц, то выборочная дисперсия
исходного
вариационного ряда увеличить на девять
единиц, то выборочная дисперсия
![]() …
…
|
|
|
|
не изменится |
|
|
|
|
увеличится в три раза |
|
|
|
|
увеличится в 81 раз |
|
|
|
|
увеличится в девять раз |
Решение:
Для
исходного вариационного ряда выборочную
дисперсию можем вычислить
по формуле
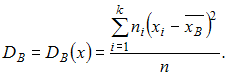 Тогда
для нового вариационного ряда
Тогда
для нового вариационного ряда
![]()
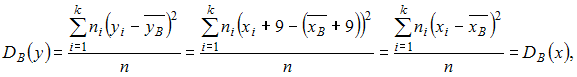 то
есть не изменится.
то
есть не изменится.
![]() ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений
Однородная
система
ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений
Однородная
система
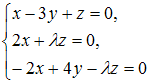 имеет
только одно нулевое решение, если
имеет
только одно нулевое решение, если
![]() принимает
значения не
равные …
принимает
значения не
равные …
|
|
|
|
2 |
|
|
|
|
– 2 |
|
|
|
|
1 |
|
|
|
|
– 1 |
![]() ЗАДАНИЕ
N 9
отправить
сообщение разработчикам
Тема:
Базис и размерность линейного
пространства
Дано
трехмерное векторное пространства с
базисом
ЗАДАНИЕ
N 9
отправить
сообщение разработчикам
Тема:
Базис и размерность линейного
пространства
Дано
трехмерное векторное пространства с
базисом
![]() Если
векторы
Если
векторы
![]() и
и
![]() то
вектор
то
вектор
![]() может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 10
отправить
сообщение разработчикам
Тема:
Умножение матриц
Даны
матрицы
ЗАДАНИЕ
N 10
отправить
сообщение разработчикам
Тема:
Умножение матриц
Даны
матрицы
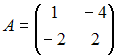 и
и
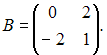 Тогда
матрица
Тогда
матрица
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Вычисление определителей
Определитель
ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Вычисление определителей
Определитель
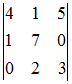 равен
…
равен
…
|
|
|
|
91 |
|
|
|
|
97 |
|
|
|
|
83 |
|
|
|
|
89 |
![]() ЗАДАНИЕ N 12
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
ЗАДАНИЕ N 12
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
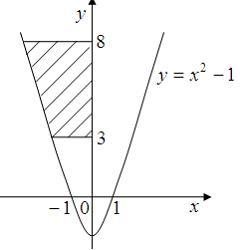 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Площадь
данной фигуры можно вычислить по формуле
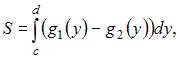 где
где
![]()
![]()
![]()
![]() Тогда
Тогда
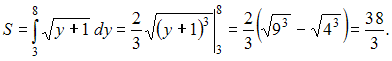
![]() ЗАДАНИЕ
N 13
отправить
сообщение разработчикам
Тема:
Непрерывность функции, точки разрыва
Функция
ЗАДАНИЕ
N 13
отправить
сообщение разработчикам
Тема:
Непрерывность функции, точки разрыва
Функция
![]() непрерывна
на отрезке …
непрерывна
на отрезке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 14
отправить
сообщение разработчикам
Тема:
Основные методы интегрирования
Множество
первообразных функции
ЗАДАНИЕ
N 14
отправить
сообщение разработчикам
Тема:
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 15
отправить
сообщение разработчикам
Тема:
Дифференциальное исчисление ФНП
Частная
производная второго порядка
ЗАДАНИЕ
N 15
отправить
сообщение разработчикам
Тема:
Дифференциальное исчисление ФНП
Частная
производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 16
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Решение
системы уравнений
ЗАДАНИЕ N 16
отправить
сообщение разработчикам
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Решение
системы уравнений
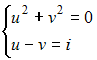 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выразим
![]() из
второго уравнения
из
второго уравнения
![]() и
подставим в первое уравнение системы
и
подставим в первое уравнение системы
![]() Получим
квадратное уравнение
Получим
квадратное уравнение
![]() Его
решения
Его
решения
![]()
![]() Соответствующие
им значения переменной
Соответствующие
им значения переменной
![]() будут
равны
будут
равны
![]()
![]() Таким
образом, решения системы будут иметь
вид:
Таким
образом, решения системы будут иметь
вид:
![]()
![]() и
и
![]()
![]()
![]() ЗАДАНИЕ N 17
отправить
сообщение разработчикам
Тема:
Дифференцирование функции комплексного
переменного
Если
ЗАДАНИЕ N 17
отправить
сообщение разработчикам
Тема:
Дифференцирование функции комплексного
переменного
Если
![]() и
и
![]() то
действительная часть производной этой
функции
то
действительная часть производной этой
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции
![]() равна
равна
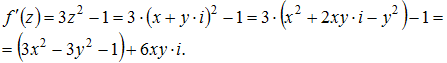 Тогда
Тогда
![]()
![]() ЗАДАНИЕ N 18
отправить
сообщение разработчикам
Тема:
Комплексные числа и их представление
Комплексное
число задано в алгебраической форме
ЗАДАНИЕ N 18
отправить
сообщение разработчикам
Тема:
Комплексные числа и их представление
Комплексное
число задано в алгебраической форме
![]() Тогда
показательная форма записи сопряженного
к нему числа
Тогда
показательная форма записи сопряженного
к нему числа
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Если
![]() то
то
![]() В
нашем случае
В
нашем случае
![]() Запись
комплексного числа в виде
Запись
комплексного числа в виде
![]() называют
показательной формой комплексного
числа. Если комплексное число записано
в форме
называют
показательной формой комплексного
числа. Если комплексное число записано
в форме
![]() то
то
![]() а
аргумент
а
аргумент
![]() определяется
из системы уравнений:
определяется
из системы уравнений:
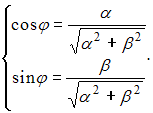 В
нашем случае
В
нашем случае
![]() и
и
![]() Тогда
Тогда
![]()
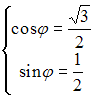 и
главное значение аргумента равно
и
главное значение аргумента равно
![]() Показательная
форма данного комплексного числа имеет
вид
Показательная
форма данного комплексного числа имеет
вид
![]()