Вариант 10

			– 22
			2
			22

  ЗАДАНИЕ N 38 отправить сообщение разработчикам Тема: Системы линейных уравнений Система  будет …

			совместной и неопределенной
			несовместной и неопределенной
			совместной и определенной
			несовместной и определенной

Решение: По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:  Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.

  ЗАДАНИЕ N 39 отправить сообщение разработчикам Тема: Комплексные числа и их представление Изображение комплексного числа z на комплексной плоскости представлено на рисунке. Тогда его алгебраическая форма записи имеет вид …

Решение: Алгебраическая форма комплексного числа имеет вид   где  – действительная часть, а  – мнимая часть комплексного числа. Так как  а  то

  ЗАДАНИЕ N 40 отправить сообщение разработчикам Тема: Системы линейных уравнений с комплексными коэффициентами Система  решается методом Крамера по формулам   Тогда вспомогательный определитель  равен …

Решение: Вспомогательный определитель  получается из определителя системы  заменой коэффициентов при переменной  на свободные члены. В нашем случае получим

 ЗАДАНИЕ N 41 отправить сообщение разработчикам Тема: Дифференцирование функции комплексного переменного Значение производной функции  в точке  равно …

  ЗАДАНИЕ N 42 отправить сообщение разработчикам Тема: Численное дифференцирование и интегрирование Значение дифференцируемой функции y = f (x) в точке  можно приближенно найти как …

Решение: Воспользуемся приближенной формулой   Тогда В нашем случае   и   Следовательно, получаем

  ЗАДАНИЕ N 43 отправить сообщение разработчикам Тема: Численные методы решения дифференциальных уравнений и систем Методом Эйлера решается задача Коши   с шагом  Тогда значение искомой функции  в точке  будет равно …

			0,82
			0,8
			0,9
			1,222

Решение: Метод Эйлера решения задачи Коши , реализуется по следующим формулам:    где  – шаг расчета (величина изменения аргумента),  а  – искомое решение задачи. Значения x₀ и y₀ для значения k = 1 определяются начальным условием задачи Коши. В нашем случае      Требуется реализовать два шага (этапа) метода Эйлера, поскольку   Тогда

  ЗАДАНИЕ N 44 отправить сообщение разработчикам Тема: Интерполирование функций: интерполяционные полиномы Лагранжа Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …

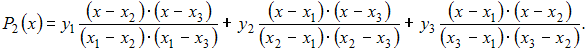Решение: Интерполяционный многочлен Лагранжа 2-ой степени для таблицы имеет вид: В нашем случае получим: