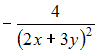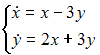Вариант 10

  ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Мера плоского множества Мера плоского множества, изображенного на рисунке,   равна …

			0

Решение: Мера плоского множества равна площади соответствующей фигуры, то есть для ее определения из площади квадрата со стороной 4 нужно вычесть площадь четвертой части круга радиуса 4. Следовательно, мера этого множества равна

  ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Метрические пространства Функция  заданная на множестве действительных чисел …

			удовлетворяет всем трем аксиомам метрического пространства
			не удовлетворяет аксиоме тождества
			не удовлетворяет аксиоме симметрии
			не удовлетворяет аксиоме треугольника

Решение: Проверим выполнение аксиом метрического пространства: А) Б) В) Пусть    Обратно   Составим неравенство треугольника для Таким образом, заданная функция удовлетворяет всем аксиомам метрики на множестве действительных чисел.

  ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Отображение множеств Образом отрезка  при отображении y = 2^x является …

			[0,5; 2]
			[– 2; 2]
			[– 0,5; 2]

Решение: Образом множества  при отображении y = 2^x являются те точки  в  которые при данном отображении попадают точки x из  В нашем случае это множество

  ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Элементы теории множеств Даны множества:  и  Тогда число элементов, принадлежащих их пересечению равно …

3 |

Решение: Определим множество  Получили множество, состоящее из трех элементов.

  ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Векторное произведение векторов Площадь треугольника, образованного векторами  и  равна …

Решение: Площадь S  треугольника, построенного на векторах  и , равна  модуля векторного произведения этих векторов, то есть  В нашем случае 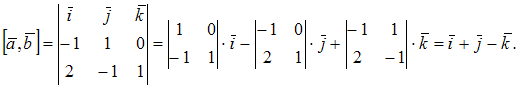Следовательно,  и

 ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Градиент скалярного поля Градиент скалярного поля  равен нулевому вектору в точке …

			(0; 0; 0)
			(– 1; 0; 1)
			(1; 1; 1)
			(0; 1; 1)

  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Норма вектора в евклидовом пространстве Если  и  – ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что   то норма вектора  равна …

			5
			25
			1
			– 1

Решение: Так как  то  и

  ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Элементы корреляционного анализа Выборочное уравнение прямой линии регрессии X на Y имеет вид  Тогда выборочный коэффициент корреляции может быть равен …

			0,71
			–0,50
			2,36
			–2,0

Решение: Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку  а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение 0,71.

 ЗАДАНИЕ N 9 отправить сообщение разработчикам Тема: Точечные оценки параметров распределения Если все варианты  исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия  …

			не изменится
			увеличится в три раза
			увеличится в 81 раз
			увеличится в девять раз

 ЗАДАНИЕ N 10 отправить сообщение разработчикам Тема: Интервальные оценки параметров распределения Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …

			(10,38; 13,70)
			(0; 13,70)
			(11,21; 12,87)
			(10,38; 12,04)

 ЗАДАНИЕ N 11 отправить сообщение разработчикам Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема n = 100: Тогда относительная частота варианты  равна …

			0,25
			0,75
			0,24
			0,04

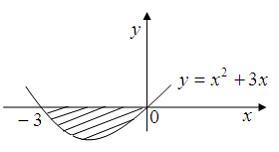  ЗАДАНИЕ N 12 отправить сообщение разработчикам Тема: Приложения определенного интеграла Площадь фигуры, изображенной на рисунке равна …

			4,5
			5,5
			10,5
			7,5

Решение: Площадь данной фигуры можно вычислить по формуле  где      Тогда

 ЗАДАНИЕ N 13 отправить сообщение разработчикам Тема: Основные методы интегрирования Множество первообразных функции  имеет вид …

 ЗАДАНИЕ N 14 отправить сообщение разработчикам Тема: Непрерывность функции, точки разрыва На отрезке  непрерывна функция …

 ЗАДАНИЕ N 15 отправить сообщение разработчикам Тема: Дифференциальное исчисление ФНП Частная производная второго порядка  функции  имеет вид …

 ЗАДАНИЕ N 16 отправить сообщение разработчикам Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …

			0

 ЗАДАНИЕ N 17 отправить сообщение разработчикам Тема: Числовые характеристики случайных величин Дискретная случайная величина  X  задана законом распределения вероятностей: Тогда ее математическое ожидание равно …

			4,6
			5,0
			3,0
			4,9

 ЗАДАНИЕ N 18 отправить сообщение разработчикам Тема: Законы распределения вероятностей дискретных случайных величин Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …

  ЗАДАНИЕ N 19 отправить сообщение разработчикам Тема: Полная вероятность. Формулы Байеса Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …

			0,57
			0,43
			0,55
			0,53

Решение: Для вычисления вероятности события  A (вынутый наудачу шар – белый) применим формулу полной вероятности: . Здесь  – вероятность того, что шар извлечен из первой серии урн;  – вероятность того, что шар извлечен из второй серии урн;  – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн;  – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн. Тогда

  ЗАДАНИЕ N 20 отправить сообщение разработчикам Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Функции  и являются решением системы дифференциальных уравнений …