1.1. Определение операторной функции arc-фильтра.

Операторная функция фильтра второго порядка имеет следующий вид:

==(1)

где - является резонансной частотой,

- нормированный по резонансной частоте операторs имеет тот же смысл что и оператор Лапласа p

Q –добротность фильтра (2)

Из формулы (1) следует, что фильтры второго порядка определяются четырьмя независимыми коэффициентами:

• Добротность Q (определяет основные характеристики фильтра);

• B0, B1, B2 – соответственно при нулевой, первой, второй степени s числителя, определяющим тип фильтра, а так же его частотные и временные свойства:

,

, (3)

Тип фильтра определяется исключительно коэффициентами числителя, что

отображено в таблице 1.

№ п/п	Тип фильтра	Коэффициенты Bk
		B0	B1	B2
1 2 3 4 5 6	ФНЧ Полосовой Фильтр (ПФ) ФВЧ Заграждающий фильтр (ЗФ) Фазовый корректор** Амплитудный корректор**	B00 B0 = 0 B0 = 0 B00 B0 = k B0 = 1	B1 = 0 B1 0 B1 = 0 B1 = 0	B2 =0 B2 =0 B2 0 B2 0 B2 =k B2 =0

Схема, для которой будет производиться расчет, представлена на Рис.1

Рис.1 Принципиальная схема ARC - фильтра второго порядка.

Преобразуем данную схему в эквивалентную операторную:

Рис.2 Эквивалентная операторная схема замещения фильтра второго порядка.

Примем за входной зажим узел 1, выходной узел 2 , а за базовый узел 4, потенциал которого равен нулю. В данной схеме операционный усилитель включен по схеме повторителя, с коэффициентом усиления .Отсюда напряжение на входеU4(p) , будет определяться выражением

с учётом направления напряжений на эквивалентной схеме. Применим метод узловых потенциалов и запишем уравнения для узлов 3 и 4:

Для схемы замещения Рис.2 справедливо равенство выходного и напряжения ИНУН, т.е. . С учётом того, что приk=подставим данное выражение в систему уравнений и получим:

Тогда первое уравнение системы принимает вид:

Откуда получается операторный коэффициент передачи по напряжению:

(5)

Обычно операторную функцию цепи представляют в канонической форме, когда коэффициент при старшей степени переменной P в знаменателе равен 1. Для этого числитель и знаменатель делится на коэффициент при старшей степениP в знаменателе. В результате чего получается:

(5’)

что соответствует выражению (1)

=(1)

Сравнивая выражения (1) и (5’) получаем:

,

,

, (6)

,

.

Таким образом, операторная функция фильтра имеет вид:

(7)

где добротность фильтра равна:

(8)

Зная коэффициенты ,,можно определить тип данного фильтра с помощью таблицы 1, из нее видно, что данный фильтр фильтром высоких частот (ФВЧ).

1.2. Рассчитать резонансную частоту f_p и добротность Q цепи. Аналитически исследовать частотные характеристики полученного ARC-фильтра, определив частоты среза и полосы пропускания и задерживания. Построить графики АЧХ и ФЧХ.

,

,

,

Q=1,39,

,(9)

Комплексная функция вида

получается заменой переменой P на jω в функции (9). Она определяет частотные свойства фильтра.

Амплитудные и фазочастотные характеристики

Заменив в формуле (1) переменную s на (илиP на jω), получим АЧХ и ФЧХ любых фильтров второго порядка:

АЧХ:

, (10)

ФЧХ: (11)

-,-

В АЧХ И ФЧХ аргументом является “нормированная” по ωр частота или частота, выраженная в относительных единицах: . В дальнейшем, если не оговорено обратное, будем использовать относительную частоту, и будем обозначать её без нижних индексов о.е. то есть просто ω.

В пункте 1.1. было получено, что для исследуемого фильтра ,b₂=0,08, подставляя в выражение (10) и (11) получаем АЧХ И ФЧХ данного фильтра:

,

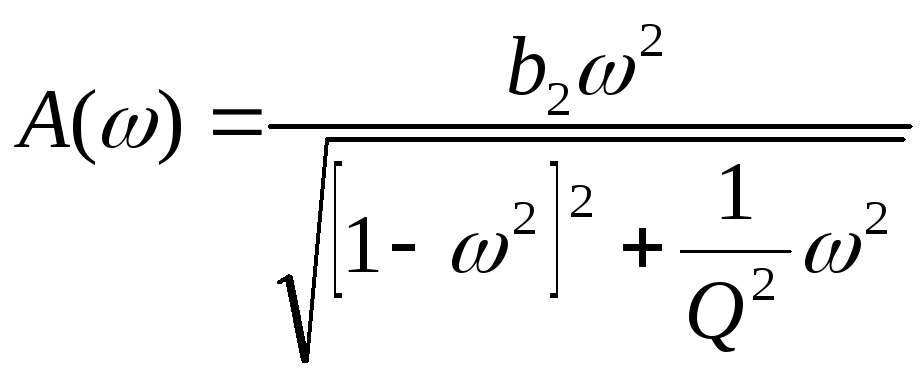Полученные АЧХ И ФЧХ соответствуют фильтру ВЧ.

Для построения графиков АЧХ и ФЧХ воспользуемся компьютерной программой MathCAD.

Рис.3. АЧХ

Для фильтра ВЧ экстремальное значение частоты _m рассчитывается по формуле:

При этом максимальные значения коэффициента передачи равно:

Полоса пропускания определяется значением АЧХ на уровне от наибольшего значения:

Частота, соответствующие значению K₁ АЧХ, и будет частотой среза _ср эту частоту можно найти графически, либо решая уравнения ( ) относительно при K=K_{u max}:

_ср=365,11 рад/с

Таким образом, полоса пропускания фильтра:

_ср<<, 1432,6 рад/с <<

А полоса задерживание соответственно будет определятся частотами:

<_ср 1432,6 рад/с

Учитывая все вышесказанное, покажем на графике полосы пропускания и задерживания:

Теперь построим график ФЧХ, с помощью Mathcad:

Рис. 4 ФЧХ

Примечание: по оси Yотложена фаза, измеряемая в радианах.