2.1.5. Диапазон регулирования скорости. Статические ошибки

Многие производственные механизмы, например, механизмы подачи и главного движения металлорежущих станков, механизмы подъемно-транспортных установок и др. требуют регулирования скорости исполнительных органов. Для таких механизмов используются регулируемые электроприводы.

Важнейшими показателями качества для регулируемого электропривода являются диапазон регулирования скорости и падение скорости от нагрузки.

Под диапазоном регулирования скорости понимают отношение верхней (наибольшей) скорости к нижней(наименьшей скорости. Под верхней и нижней скоростями обычно понимают задаваемые значения угловых скоростей на холостом ходу (см. рис. 2.8)

. (2.8)

Например, если электропривод имеет верхнюю скорость =1000об/мин иD =1000, то нижняя скорость обмин.

Падение скорости под нагрузкой (см. рис.2.8) определяют обычно при номинальном значении нагрузки (момента). Величинуназывают такжеабсолютной статической ошибкой от нагрузки. Для оценки качества работы электропривода удобнее использовать значение относительной статической ошибки от нагрузки.

Относительная ошибка определяется обычно в процентах по выражению

,

где - заданное значение угловой скорости или частоты вращения.

Значение абсолютной ошибки на верхней и нижней характеристиках, как правило, одно и то же. При этом относительная ошибка на верхней скорости

, (2.9)

а на нижней

(2.10)

Используя выражения (2.9) и (2.10), найдем отношение

.

Тогда, с учетом выражения (2.9) для диапазона регулирования, получим

. (2.11)

Таким образом, относительная статическая ошибка от нагрузки на нижней скорости в D раз больше, чем на верхней.

Производственные механизмы, как правило, требуют поддержания скорости с заданной точностью во всем диапазоне регулирования. Отсюда следует, что при проектировании электропривода нужно прежде всего обеспечить требуемую точность стабилизации на нижней скорости.

2. 2. Механические характеристики и способы регулирования скорости двигателей постоянного тока (дпт) независимого возбуждения (нв)

2.2.1. Электромеханические и механические характеристики дпт нв

Схема подключения ДПТ НВ приведена на рис. 2.9. Напряжение U_я на якорь двигателя М с электромагнитным возбуждением подается от подключенного к сети переменного тока преобразователя (выпрямителя) П1.

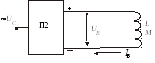
Рис.2.9

(предполагается, что он нерегулируемый). Обмотка возбуждения LM двигателя может быть подключена к другому преобразователю П2 или к точкам а, в первого преобразователя. При наличии сети постоянного тока якорь и обмотка возбуждения так же получают питание от одного источника.

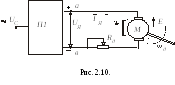
Для подключения машины с возбуждением от постоянных магнитов (см. рис. 2.10) достаточно одного преобразователя. В цепь якоря при питании его от неуправляемого преобразователя обычно включается добавочное сопротивление R_д (его назначение поясняется ниже).

В двигательном режиме электрическая энергия потребляется машиной из сети и преобразуется в механическую энергию.

Направление тока якоря I_я и ЭДС Е рис.2.9, 2.10 показано для двигательного режима.

Напряжение U_я (В), приложенное к якорю, в установившемся режиме уравновешивается ЭДС Е (В), наведенной в якоре (ее называют также противоЭДС), и падением напряжения в якорной цепи

U_я = Е + I_я(R_я+R_д), (2.12)

где R_я – сопротивление якорной цепи двигателя, Ом, включающее сопротивления обмотки якоря, щеточного контакта, дополнительных полюсов и компенсационной обмотки; R_д – добавочное сопротивление.

ЭДС машины определяется соотношением

Е= сФ_д, (2.13)

здесь конструктивный коэффициент

с = рN/ 2а,

р – число пар полюсов;

N – число активных проводников обмотки якоря;

а – число пар параллельных ветвей обмотки якоря;

Ф – магнитный поток, Вб, создаваемый обмоткой возбуждения или постоянными магнитами.

Подставляя выражение (2.13) для Е в уравнение (2.12) и решая его относительно _д, получим:

_д = . (2.14)

Это уравнение устанавливает связь между частотой вращения и током якоря _д = f(Iя) и называется электромеханической характеристикой двигателя.

Электромагнитный момент двигателя (Нм), определяется током якоря и магнитным потоком:

М = сФI_я. (2.15)

Момент на валу двигателя меньше электромагнитного на значение, определяемое потерями в стали и механическими потерями. Для инженерных расчетов этими потерями можно пренебречь, и принять, что момент на валу равен электромагнитному моменту. Тогда, определив из (2.15) ток якоря и подставив его в соотношение (2.14), получим уравнение механической характеристики двигателя:

_д = . (2.16)

Полученные выражения (2.14), (2.16) для характеристик двигателя представляют собой уравнение прямой. Они справедливы, если пренебречь реакцией якоря.

В уравнениях (2.14), (2.16) первое слагаемое представляет собой угловую скорость идеального холостого хода (при этом ток якоря и момент равны 0)

₀ = . (2.17)

Второй член в этих уравнениях характеризует статическое падение угловой скорости от нагрузки

или (2.18)

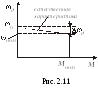
На рис. 2.11 падение скорости показано для номинального значения момента M_ном (тока I_ном). При неизменном магнитном потоке момент и ток якоря, как следует из соотношения (2.15) пропорциональны. Поэтому механическая и электромеханическая характеристики двигателя (см. рис. 2.11) отличаются только масштабом по оси ординат. Характеристика, полученная при номинальном значении напряжения на якоре U_ном, номинальном магнитном потоке Ф_ном и отсутствие внешних резисторов в якорной цепи, называется естественной. Жесткость естественной характеристики определяется только сопротивлением якорной цепи двигателя:

или . (2.19)

Снижение скорости _д под нагрузкой объясняется следующим. При увеличении момента сопротивления механизма угловая скорость начинает снижаться. В результате уменьшается ЭДС Е согласно (2.13). Ток якоря при этом, как следует из (2.12) увеличивается. Соответственно возрастает момент двигателя (см. уравнение (2.15)). Этот процесс продолжается до тех пор, пока момент двигателя не сравняется с моментом сопротивления. После достижения равенства М=М_с наступит новый установившийся режим с меньшей угловой скоростью _д.

При инженерных расчетах коэффициенты, входящие в уравнения характеристик двигателя, могут быть определены через номинальные параметры двигателя, приводимые в каталогах. При номинальном магнитном потоке

(2.20)

Здесь коэффициент К_д - коэффициент передачи двигателя, его размерность . С использованием этого понятия уравнения (2.14), (2.16) могут быть переписаны в виде:

(2.21)

(2.22)

В этих уравнениях, как и в (2.14, 2.16), первый член представляет собой угловую скорость идеального холостого хода, а второй – падение скорости от нагрузки:

, (2.23)

или

(2.24)

Пример. Известны номинальные данные двигателя:

Рассчитать естественную характеристику двигателя.

Находим номинальную угловую скорость

Коэффициент передачи двигателя по (2.9)

.

Угловая скорость на холостом ходу при номинальном напряжении с учетом (2.23)

Полученных результатов () достаточно для построения характеристики (см. рис. 2.11). Для проверки находим по (2.13) падение угловой скорости при номинальном токе

а так же вычислим по очевидному соотношению

Совпадение результатов подтверждает правильность вычислений.

Для построения механической характеристики необходимо дополнительно рассчитать с учетом (2.2) номинальный момент двигателя