2.3.4 Регуляторы в системах эп

Как уже отмечалось, современные АЭП выполняются в виде замкнутых систем автоматического управления. При этом возникает задача обеспечения устойчивости замкнутой системы и требуемых показателей качества регулирования. Эти задачи решаются введением в систему операционных усилителей, охваченных определенными видами обратных связей. Такие усилители в системах автоматического регулирования принято называтьрегуляторами. Кроме того, на входе усилителя удобно осуществлять операцию сравнивания электрических сигналов. Схемасуммирующего усилителяприведена на рис. 2.30. На инвертирующий вход (на схеме помечен окружностью)DАусилителя подается: через резисторR1– сигнал заданияU_зд; через резисторR2– сигнал отрицательной обратной связиU_ос(например, сигнал обратной связи по скорости двигателя). Известно, что динамические свойства операционного усилителя, охваченного обратной связью, приближенно можно описать передаточной функцией

, (2.42)

где ,Z_вх(p)– операторное сопротивление обратной связи усилителя и входной цепи, соответственно.

Для рассматриваемой схемы , для задающего сигналаZ_вх(p)=R1, сигнала обратной связиZ¹_ос(p)=R2. В результате передаточная функция регулятора вырождается в коэффициент передачи. Причем, еслиR1=R2, то коэффициент передачи по обоим входам усилителя один и тот же

.

Напряжение на выходе усилителя

U_вых = U_здK_у – U_осK_у = (U_зд – U_ос)K_у.

Последнему выражению соответствует алгоритмическая схема, представленная на рис. 2.31. Из нее следует, что рассматриваемая схема обеспечивает сравнение (вычитание) напряжений и усиление сигнала ошибки U_δ=U_зд – U_ос. Приведенную схему (см. рис. 2.30) называютпропорциональным регулятором, или сокращенноП-регулятором.

R3

U_вых

DA

к1

U_зд

U_ос

R2

Рис. 2.30

U_зд(p)

U_ос(p)

U_(p)

K_у

U_вых(p)

Рис. 2.31

R3

R1

R2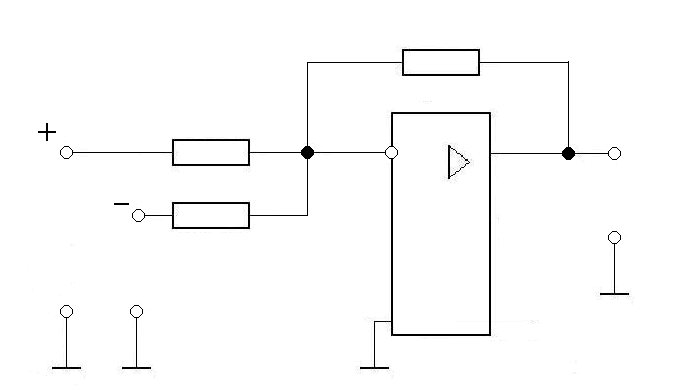

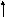
Для уменьшения статистической ошибки, как отмечалось выше, необходимо вводить в систему интегрирующее звено. Схема интегрального регулятора(И-регулятора) приведена на рис. 2.32 (для простоты считаем здесь и далееR1=R2). На основании выражения (2.42) несложно получить передаточную функцию регулятора

,

где Т_и– постоянная времени интегрирующего преобразования.

Передаточная функция соответствует интегрирующему (астатическому) звену.

При скачкообразном изменении сигнала U_напряжениеU_выхлинейно нарастает (см. рис. 2.33). Учитывая свойства И-регулятора «накапливать» входной сигнал, можно дать следующие пояснение особенностям работы астатической системы. Если в системе появляется сигнал ошибки, то напряжение на выходе регулятора начинает изменяться и, соответственно, изменяется воздействие на двигатель. Этот процесс продолжается до тех пор, пока сигнал ошибки не будет сведен к нулю, т.е. пока не будет достигнуто равенство

U_ос = U_зд.

В

ыполнение же этого равенства означает, что регулируемая величина равна заданной, т.е. статистическая ошибка системы сведена к нулю. Отметим, что для сведения статистической ошибки к нулю нужен идеальный И-регулятор. В реальной схеме операция интегрирования выполняется с некоторой погрешностью, поэтому статистическая ошибка в замкнутой системе сводится не до нуля, но, как правило, до достаточно малых значений.

Алгоритмическая схема регулятора приведена на рис. 2.34. И-регулятор обеспечивает сравнение сигналов U_здиU_ос, а его выходное напряжение пропорционально интегралу от сигнала ошибки.

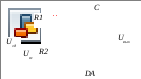
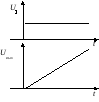
Рис. 2.32

Рис. 2.33

U_зд(p)

U_(p)

U_вых(p)

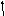
С

U_ос(p)

Рис. 2.34

хемапропорционально-интегрального регулятора (ПИ-регулятора)приведена на рис. 2.35. В цепь обратной связи операционного усилителя последовательно включены резисторR3и емкостьС. На основании выражения (2.42) несложно найти передаточную функцию регулятора

, (2.43)

где T =R3C, T_и = R2С– соответственно, постоянные времени дифференцирующего и интегрирующего преобразования.

С

t

t

U_зд - U_oc

К

R3

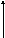
R1

U_вых

U_вых

U_зд

R2

U_ос

DA

Рис. 2.36

Рис. 2.35

Передаточную функцию (2.43) можно

исать и в другом виде. Деля почленн

Выражение (2.43) можно записать и в другом виде, деля почленно числитель на знаменатель, получим

,

где K=T/T_и – коэффициент усиления пропорциональной части регулятора. Как следует из последнего выражения, передаточную функцию можно представить в виде суммы пропорциональной части (П) и интегральной (И) части. Отсюда название регулятора. Реакция ПИ-регулятора на скачкообразное изменение сигнала(U_зд - U_oc)приведена на рис. 2.36. Сравнивая рис. 2.34 и рис. 2.36, можно отметить, что ПИ-регулятор в первый момент времени более «энергично» воздействует на управляемый преобразователь и, соответственно, двигатель. Благодаря этому, в принципе, быстродействие системы может быть улучшено.

Схема пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора) приведена на рис. 2.37. По сравнению с предыдущей схемой здесь добавлены емкостиС2иС3, включенные параллельно резисторамR1, R2. Иногда емкость включают только параллельноR2. Тогда для сигнала обратной связи схема имеет свойства ПИД- регулятора, а для сигнала задания – свойства ПИ- регулятора.

Используя выражение (2.42), передаточную функцию рассматриваемого регулятора можно записать в виде

, (2.44)

где постоянные времени дифференцирования Т1, Т2 и интегрирования Т_и определяются соотношениями:

Т₁ = R3C1; T₂ = R2C3; T_и = R2C1.