5.6. Формула Бернулли

Опыты называются независимыми, если вероятность исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Пусть проводятся n независимых опытов, в результате которых может появиться событие A с вероятностью p и не появиться с вероятностью q, причем p+q = 1. Такая схема называется схемой Бернулли.

Пусть X – число появлений события А в n испытаниях Бернулли. Тогда вероятность того, что в серии из п независимых испытаний событие А появится ровно раз (Х=k) вычисляется по формуле Бернулли:

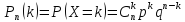
Пример:

_________________________________________________________ _

Вероятность попадания в мишень для конкретного стрелка равна 0,7. Какова вероятность того, что из 10 выстрелов будет 4 попадания в мишень?

Воспользуемся формулой Бернулли при k = 4, n = 10, p = 0,7. Искомая вероятность равна 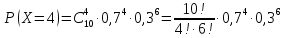= 0,0367.

________________________________________________________________

В n испытаниях Бернулли наивероятнейшее число k₀ появления события А определяется неравенством

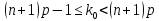
Пример:

________________________________________________________ ___

Всхожесть семян некоторого растения имеет вероятность 0,8. Найти наиболее вероятное число проросших семян из 7 посеянных.

По формуле 8 ∙ 0,8-1, поэтому = 6.

______________________________________________________________

5.7. Формула Пуассона

Если в схеме испытаний Бернулли число испытаний n велико, вероятность p события A в одном испытании мала, а произведение λ = np не превосходит 20, то вероятность 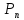(m) того, что событие A появится ровно в m испытаниях, находится по приближенной формуле Пуассона:

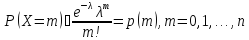
Значения имеются в таблицах значений функции Пуассона.

Пример:

______________________________________________________ __

В ходе проверки случайным образом отбирается 10 счетов. Найти вероятность того, что обнаружится один счет с ошибкой, если в среднем 3% счетов содержат ошибки.

Для решения задачи используем формулу Пуассона, в которой n = 10, p=0,03, λ = np = 0,3. Имеем

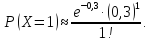
По таблицам значений функции Пуассона находим 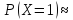0,2223.

5.8. Локальная формула Муавра – Лапласа

Если число испытаний n достаточно велико, то вероятность появления события A ровно m раз в схеме из n испытаний Бернулли можно вычислять по приближенной формуле Муавра – Лапласа:

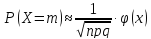где

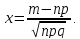
Причем 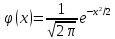– малая функция Лапласа (функция Гаусса), значения которой имеются в соответствующих таблицах.

Пример: _________________________________________________________ _

Вероятность найти белый гриб среди прочих равна 0,25. Какова вероятность того, что среди 70 грибов белых будет 20?

По формуле Муавра – Лапласа при n=70, m=20 имеем:

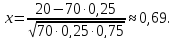
По таблицам определяем значение 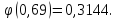Тогда

.

______________________________________________________________
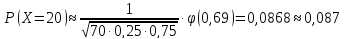