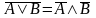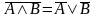Вопрос 8. Сумматор
Основной элементарной операцией,
выполняемой над кодами чисел в цифровых
устройствах, является арифметическое
сложение. Сумматор — логический
операционный узел, выполняющий
арифметическое сложение кодов двух
чисел. При арифметическом сложении
выполняются и другие дополнительные
операции: учёт знаков чисел, выравнивание
порядков слагаемых и тому подобное.
Указанные операции выполняются в
арифметическо-логических устройствах
(АЛУ) или процессорных элементах, ядром
которых являются сумматоры.
Сумматоры
классифицируют по различным признакам:
По
количеству одновременно обрабатываемых
разрядов складываемых чисел:
одноразрядные,
многоразрядные.
По
числу входов и выходов одноразрядных
двоичных сумматоров:
четвертьсумматоры
полусумматоры, характеризующиеся
наличием двух входов, на которые подаются
одноимённые разряды двух чисел, и двух
выходов: на одном реализуется
арифметическая сумма в данном разряде,
а на другом — перенос в следующий (более
старший разряд);
полные одноразрядные двоичные сумматоры,
характеризующиеся наличием трёх входов,
на которые подаются одноимённые разряды
двух складываемых чисел и перенос из
предыдущего (более младшего) разряда,
и двумя выходами: на одном реализуется
арифметическая сумма в данном разряде,
а на другом — перенос в следующий (более
старший разряд).
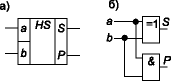
Полусумматор
имеет два входа a и b для двух слагаемых
и два выхода: S — сумма, P — перенос.
Обозначением полусумматора служат
буквы HS (half sum — полусумма). Работу его
отражает таблица истинности.
a b P S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
Вопрос 9 Законы логики
Основные
законы логики :
А = А – закон тождества
А &
 =
0 – закон непротиворечия
=
0 – закон непротиворечия
A
= 1 – закон исключенного третьего
 = А – закон двойного отрицания
= А – закон двойного отрицания
Свойства констант:
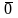 =
1
=
1
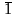 =
0
=
0
А 0 = А А
0 = 0
А 1 = 1 А
1 = 1
Законы идемпотентности:
А А = А
А
А = A
Законы коммутативности:
А В = В
А
А В = В
А
Законы ассоциативности:
А (В
С) = (А В)
С
А (В
С) = (А В)
С
Законы дистрибутивности:
А (В
С) = (А В)
(А С)
А (В
С) = (А В)
(А С)
Законы поглощения:
А (А
В) = А
А (А
В) = А
Законы де Моргана:
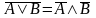
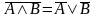



 =
0 – закон непротиворечия
=
0 – закон непротиворечия = А – закон двойного отрицания
= А – закон двойного отрицания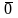 =
1
=
1
 =
0
=
0