МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра МНЭ
отчёт
по индивидуальному заданию №4
по дисциплине «Моделирование и проектирование микро- и наносистем»
Тема: Численное решение фундаментальной системы уравнений полупроводника в диффузионно-дрейфовом приближении для моделирования стационарных процессов в p-n-переходе
Вариант №16
Студентка гр. 9282 |
|
Зикратова А. А. |
Преподаватель |
|
Рындин Е. А. |
Санкт-Петербург
2022
Цель работы.
Численное моделирование стационарных процессов в p-n-переходе. Построение вольт-амперной характеристики (ВАХ) и пространственных распределений электростатического потенциала и концентраций электронов и дырок для каждой точки ВАХ полупроводникового р-n-перехода.
Задание.
Таблица 1 - Исходные данные
№ п/п |
Полупроводник |
Длина n-области Ln, нм |
Длина p-области Lp, нм |
Концентрация легирующей примеси в n-области ND, см-3 |
Концентрация легирующей примеси в p-области NA, см-3 |
Диапазон напряжений U, В |
Температура кристалла T, К |
16. |
Арсенид галлия (GaAs) |
200 |
200 |
1 * 1017 |
1 * 1017 |
0 – 0,8 |
350 |
n - область
p - область
x
y
z
xmax
xmin
Рис. 1 – Общий вид полупроводниковой структуры
Теоретические положения.
Ⅰ. Система уравнений и граничные условия в обычном виде, без нормировки:
Данная система состоит из уравнения Пуассона, которое описывает распределение потенциала в кристалле, и уравнений непрерывности для концентраций электронов и дырок.
Граничные условия для концентраций:
Граничные условия для потенциала:
→
→ →
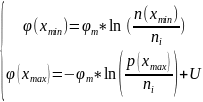- при подаче на
p-область
напряжения U,
а на n-область
0
Порядки расчётных величин могут сильно различаться → проводится нормировка
Таблица 2 – Данные для нормировки |
|
Нормируемая величина |
Нормирующий коэффициент |
x |
L0
=
|
t |
τ0 |
φ, U |
φт
=
|
n, p, N |
ni |
μn, μp |
μ0
=
|
jn, jp |
j0
=
|
n =
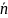*ni,
p =
*ni,
φ =
*φт,
x =
*L0
Для удобства переобозначим: → n, → p, → φ, → x
Ⅱ. Система уравнений и граничные условия в обычном виде с учётом нормировки:
Граничные условия для концентраций и потенциала:
Из базиса
перейдём в базис
для улучшения сходимости, где:
→
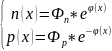- нормированная
система уравнений в новом базисе.
Граничные условия для концентраций и потенциала в новом базисе:
Ⅲ. Система уравнений и граничные условия в дискретном виде с учётом нормировки:
,
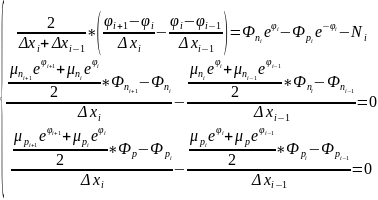где
I = 2…I – 1
,
где j
= 1…J
Для решения данной системы используется итерационный метод Гуммеля:
1) задаётся начальное
приближение
(задавали линейное приближение
)
и подставляется в уравнение непрерывности
2) решается система уравнений относительно экспонент квазиуровней Ферми с учётом начального приближения
3) по полученным
значениям ищется следующее приближение
и так на каждом шаге
Оценка приближения к решению (невязка):
=
Программа в Matlab:
clear all
close all
clc
q=1.6e-19;
eps0=8.85e-12;
eps=12.9;
kB=1.38e-23;
h=6.6262e-34;
me=9.1e-31;
T=350;
ft=kB*T/q;
mnt=0.19;
mnl=0.98;
m1n=0.009;
mph=0.49;
mpl=0.16;
m1p=0.6;
m2p=-0.1;
m0n=(mnt^2*mnl)^(1/3);
m0p=(mpl^1.5+mph^1.5)^(2/3);
mn=m0n+m1n*(T/300);
mp=m0p+m1p*(T/300)+m2p*(T/300)^2;
Nc=2*(2*pi*mn*me*kB*T/h^2)^1.5;
Nv=2*(2*pi*mp*me*kB*T/h^2)^1.5;
Eg0=1.519;
a=5.41e-4;
b=204;
Eg=Eg0-a*T^2/(b+T);
ni=sqrt(Nc*Nv)*exp(-Eg/2/ft);
t0=1e-6;
L0=sqrt(eps*eps0*ft/q/ni);
mu0=L0^2/ft/t0;
J0=q*ni*mu0*ft/L0;
Mun=1400*1e-4;
Mup=500*1e-4;
L=[200 200];
L=L.*1e-9;
Nd=[1e17 1e14];
Na=[1e14 1e17];
Nef=(Nd-Na).*1e6;
U=[0 0.2 0.3 0.4 0.5 0.6 0.65 0.7 0.75 0.78 0.8];
K=[200 200 200 200 200 200 200 200 200 200 200];
FS=19;
U=U/ft;
Delta=1e-6;
Sx=100;
(1)=0;
N(1)=Nef(1);
for i=1:length(L)
x=[x max(x)+L(i)/Sx:L(i)/Sx:max(x)+L(i)];
N=[N ones(1,Sx).*Nef(i)];
end
dx=diff(x);
I=length(x);
mun=ones(1,I).*Mun;
mup=ones(1,I).*Mup;
x=x./L0;
dx=dx./L0;
N=N./ni;
mun=mun./mu0;
mup=mup./mu0;
fi0=zeros(I,1);
(1)=log(N(1)/2+sqrt((N(1)/2)^2+1));
fi0(I)=-log(-N(I)/2+sqrt((N(I)/2)^2+1))+U(1);
for i=2:I-1
fi0(i)=fi0(1)+(fi0(I)-fi0(1))/(x(I)-x(1))*(x(i)-x(1));
end
plot(x.*(L0*1e9),fi0.*ft,'LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('\phi, V','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
pause(1e-3)
NN='pn_';
for j=1:length(U)
if j>1
for i=1:I
fi0(i)=fi0(i)+((fi0(i)-fi0(1))/(fi0(I)-fi0(1)))*(U(j)-U(j-1)); end
end
err=10*Delta;
ct=0;
while err>Delta
if U(j)==0
Fn=ones(I,1);
Fp=ones(I,1);
else
A=zeros(I,I);
B=zeros(I,1);
A(1,1)=1;
B(1)=1;
A(I,I)=1;
B(I)=exp(-U(j));
for i=2:I-1
A(i,i)=-mun(i)*exp(fi0(i))/dx(i)-mun(i-1)*exp(fi0(i-1))/dx(i-1);
A(i,i+1)=mun(i)*exp(fi0(i))/dx(i);
A(i,i-1)=mun(i-1)*exp(fi0(i-1))/dx(i-1);
B(i)=0;
end
Fn=A^(-1)*B;
A=zeros(I,I);
B=zeros(I,1);
A(1,1)=1;
B(1)=1;
A(I,I)=1;
B(I)=exp(U(j));
for i=2:I-1
A(i,i)=-mup(i)*exp(-fi0(i))/dx(i)-mup(i-1)*exp(-fi0(i-1))/dx(i-1);
A(i,i+1)=mup(i)*exp(-fi0(i))/dx(i);
A(i,i-1)=mup(i-1)*exp(-fi0(i-1))/dx(i-1);
B(i)=0;
end
Fp=A^(-1)*B;
end
A=zeros(I,I);
B=zeros(I,1);
A(1,1)=1;
B(1)=fi0(1);
A(I,I)=1;
B(I)=fi0(I);
for i=2:I-1
A(i,i)=2/(dx(i)+dx(i-1))*((-1)/dx(i)-1/dx(i-1));
A(i,i+1)=2/(dx(i)+dx(i-1))/dx(i);
A(i,i-1)=2/(dx(i)+dx(i-1))/dx(i-1);
B(i)=Fn(i)*exp(fi0(i))-Fp(i)*exp(-fi0(i))-N(i);
end
fi=A^(-1)*B;
clc
err=max(abs(fi-fi0))/max(abs(fi0))
Voltage=U(j)*ft
fi0=fi0+(fi-fi0)./K(j);
end
n=Fn.*exp(fi0);
p=Fp.*exp(-fi0);
for i=1:I-1
E(i)=-(fi0(i+1)-fi0(i))/dx(i);
end
E(I)=E(I-1);
RO=p-n+N';
for i=1:I-1
Jn(i)=-mun(i)*exp(fi0(i))*(Fn(i+1)-Fn(i))/dx(i);
Jp(i)=mup(i)*exp(-fi0(i))*(Fp(i+1)-Fp(i))/dx(i);
end
Jn(I)=Jn(I-1);
Jp(I)=Jp(I-1);
J=Jn+Jp;
Jvah(j)=J(I);
NNN=[NN num2str(j)];
subplot(2,3,1)
plot(x.*(L0*1e9),-fi0.*ft+Eg/2, x.*(L0*1e9),-fi0.*ft-Eg/2, x.*(L0*1e9),-fi0.*ft, '--','LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('Zones, eV','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,2)
plot(x.*(L0*1e9),n.*(ni*1e-6),x.*(L0*1e9),p.*(ni*1e-6),'LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('Consentrations, cm^-3','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,3)
semilogy(x.*(L0*1e9),n.*(ni*1e-6),x.*(L0*1e9),p.*(ni*1e-6),'LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('Consentrations, cm^-3','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,4)
plot(x.*(L0*1e9),E.*(ft*1e-2),'LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('Field, V/cm','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,5)
plot(x.*(L0*1e9),RO.*(ni*q*1e-6),'LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('Charge density, C/cm^3','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,6)
semilogy(x.*(L0*1e9),J.*(J0*1e-4),'LineWidth',3)
xlabel('x, nm','FontSize', FS);
ylabel('Current density, A/cm^2','FontSize', FS);
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
set(gcf, 'Position', [7 70 1200 500]);
print(gcf, '-djpeg', NNN);
pause(1e-3)
end
figure
plot(U.*ft,Jvah.*(J0*1e-4),'LineWidth',3)
xlabel('Voltage, V','FontSize', FS);
ylabel('Current density, A/cm^3','FontSize', FS);
xlim([min(U.*ft) max(U.*ft)])
grid on
print(gcf, '-djpeg', 'VAH')