ИДЗ_3_С использованием неявной схемы

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра МНЭ

отчёт

по индивидуальному заданию №3

по дисциплине «Моделирование и проектирование микро- и наносистем»

Тема: Численное моделирование нестационарного процесса теплопроводности в неоднородном теле с учетом зависимости плотности мощности источников (стоков) тепла от температуры с использованием неявной схемы

Вариант №16

Студентка гр. 9282		Зикратова А. А.
Преподаватель		Рындин Е. А.

Санкт-Петербург

2022

Цель работы.

Численное моделирование нестационарного процесса теплопроводности в неоднородном теле с использованием прямых методов решения СЛАУ. Нахождение распределения температуры в многослойной структуре в каждый момент времени из заданного диапазона.

Задание.

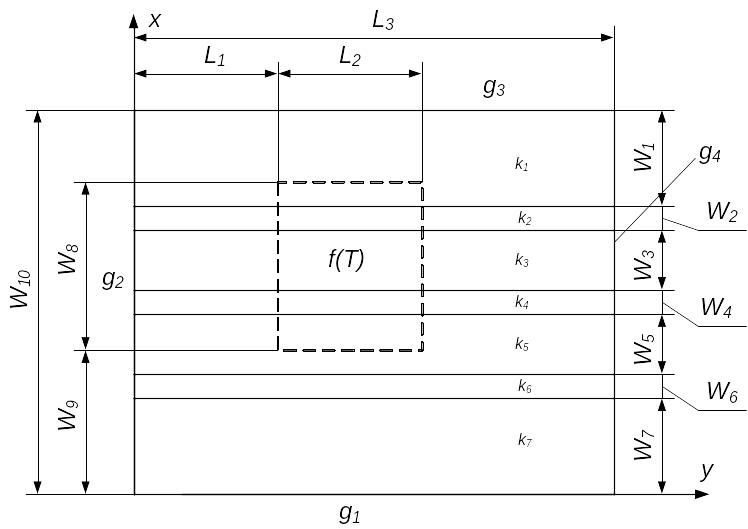
Рис. 1 – Общий вид неоднородной структуры

Таблица 1 – Исходные данные

№ п/п	L, мм	W, мм	Коэффициент теплопроводности k, Вт/(м К)	Плотность , кг/м3	Удельная теплоемкость C, Дж/(кг К)	Начальное и граничные условия (род) gt gxmin gxmax gymin gymax, К или К/м	Зависимость плотности мощности источников (стоков) тепла от температуры f(T), Вт/м3	Интервал времени t, c
16.	30 150 230	10 10 20 10 50 10 20 30 30 130	1000 100 200 100 300 10 10000	10000 2000 1000 2000 1000 2000 300	10000 100 1000 100 1000 100 300	300(1) 50(2) 50(2) 300(1) 0(2)	-1107 (ИДЗ №1) -1107/lgT (ИДЗ №2,3)	20

Теоретические положения.

Ⅰ. Уравнение и условия в обычном виде:

- -

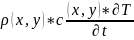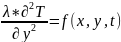
Начальное условие:

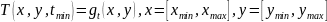
Г

} y = [y_min, y_max], t = (t_min, t_max]

раничные условия:

1)

2)

3

} x = (x_min, x_max), t = (t_min, t_max]

)

4)

Ⅱ. Уравнение и условия в дискретном виде:

↓

= - в следующий момент времени, = 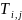– в предыдущий момент времени → можно отбросить индекс «m» и последовательно находить температуры в точках (i, j) по временным срезам. На каждом шаге по времени решается СЛАУ.

↓

Начальное условие:

,

Граничные условия:

1

} j = 1…J

} i = 2…I - 1

) 3) =

2) 4) =

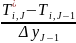Программа в Matlab:

clear all

close all

clc

L=[30 150 230];

L=L.*1e-3;

W=[10 10 20 10 50 10 20 30 30 130];

W=W.*1e-3;

kL=[1000 100 200 100 300 10 10000];

rL=[10000 2000 1000 2000 1000 2000 300];

cL=[10000 100 1000 100 1000 100 300];

gt=300;

gxmin=50;

gxmax=50;

gymin=300;

gymax=0;

F=-1e7;

tmax=20;

dt=1e-1;

b=16;

Sx=7;

kV(1)=kL(1);

rV(1)=rL(1);

cV(1)=cL(1);

x(1)=0;

for i=1:length(kL)

x=[x max(x)+W(i)/Sx:W(i)/Sx:max(x)+W(i)];

kV=[kV ones(1, Sx).*kL(i)];

rV=[rV ones(1, Sx).*rL(i)];

cV=[cV ones(1, Sx).*cL(i)];

end

kV=kV';

rV=rV';

cV=cV';

I=length(x);

dx=diff(x);

L(3)=L(3)-L(1)-L(2);

Sy=9;

y(1)=0;

for i=1:length(L)

y=[y max(y)+L(i)/Sy:L(i)/Sy:max(y)+L(i)];

end

J=length(y);

dy=diff(y);

k=kV;

r=rV;

c=cV;

for j=2:J

k=[k kV];

r=[r rV];

c=[c cV];

end

t=0;

T0=ones(I,J).*gt;

ct=1;

NN='Graphic_';

NNN=[NN num2str(ct)];

figure

mesh(y.*1e3, x.*1e3, T0-273)

xlabel('y, mm','FontSize',19)

ylabel('x, mm','FontSize',19)

zlabel('T, ^oC','FontSize',19)

xlim([min(y.*1e3) max(y.*1e3)])

ylim([min(x.*1e3) max(x.*1e3)])

zlim([-20 100])

grid on

colormap([0 0 0])

print(gcf, '-djpeg', NNN)

pause(1e-3)

ct=1;

while t<=tmax

t=t+dt;

ct=ct+1;

f=zeros(I,J);

for j=Sy+1:2*Sy+1

for i=1:I

if x(i)>=W(9) && x(i)<=W(9)+W(8)

f(i,j)=F;

end

end

end

A=zeros(I*J,I*J);

B=zeros(I*J,1);

for i=2:I-1

A(I*(1-1)+i, I*(1-1)+i)=1;

B(I*(1-1)+i)=gymin;

end

for j=1:J

A(I*(j-1)+1, I*(j-1)+1)=-1/dx(1);

A(I*(j-1)+1, I*(j-1)+1+1)=1/dx(1);

B(I*(j-1)+1)=gxmin;

A(I*(j-1)+I, I*(j-1)+I)=1/dx(I-1);

A(I*(j-1)+I, I*(j-1)+I-1)=-1/dx(I-1);

B(I*(j-1)+I)=gxmax;

end

for i=2:I-1

A(I*(J-1)+i, I*(J-1)+i)=1/dy(J-1);

A(I*(J-1)+i, I*(J-1-1)+i)=-1/dy(J-1);

B(I*(J-1)+i)=gymax;

end

for i=2:I-1

for j=2:J-1

A(I*(j-1)+i, I*(j-1)+i)=r(i,j)*c(i,j)/dt-...

2/(dx(i)+dx(i-1))*(-k(i,j)/dx(i)-k(i-1,j)/dx(i-1))-...

2/(dy(j)+dy(j-1))*(-k(i,j)/dy(j)-k(i,j-1)/dy(j-1));

A(I*(j-1)+i, I*(j-1)+i+1)=-2/(dx(i)+dx(i-1))*k(i,j)/dx(i);

A(I*(j-1)+i, I*(j-1)+i-1)=-2/(dx(i)+dx(i-1))*k(i-1,j)/dx(i-1);

A(I*(j-1)+i, I*(j+1-1)+i)=-2/(dy(j)+dy(j-1))*k(i,j)/dy(j);

A(I*(j-1)+i, I*(j-1-1)+i)=-2/(dy(j)+dy(j-1))*k(i,j-1)/dy(j-1);

B(I*(j-1)+i)=f(i,j)+r(i,j)*c(i,j)/dt*T0(i,j);

end

end

TV=A^(-1)*B;

for i=1:I

for j=1:J

T(i,j)=TV(I*(j-1)+i);

end

end

T0=T;

NN='Graphic_';

NNN=[NN num2str(ct)]

if ct/b-fix(ct/b) == 0

NNN=[NN num2str(fix(ct/b)+1)];

figure

mesh(y.*1e3, x.*1e3, T-273)

xlabel('y, mm','FontSize',19)

ylabel('x, mm','FontSize',19)

zlabel('T, ^oC','FontSize',19)

xlim([min(y.*1e3) max(y.*1e3)])

ylim([min(x.*1e3) max(x.*1e3)])

zlim([-20 100])

grid on

colormap([0 0 0])

pause(1e-3)

print(gcf, '-djpeg', NNN)

end

end

Результаты моделирования:

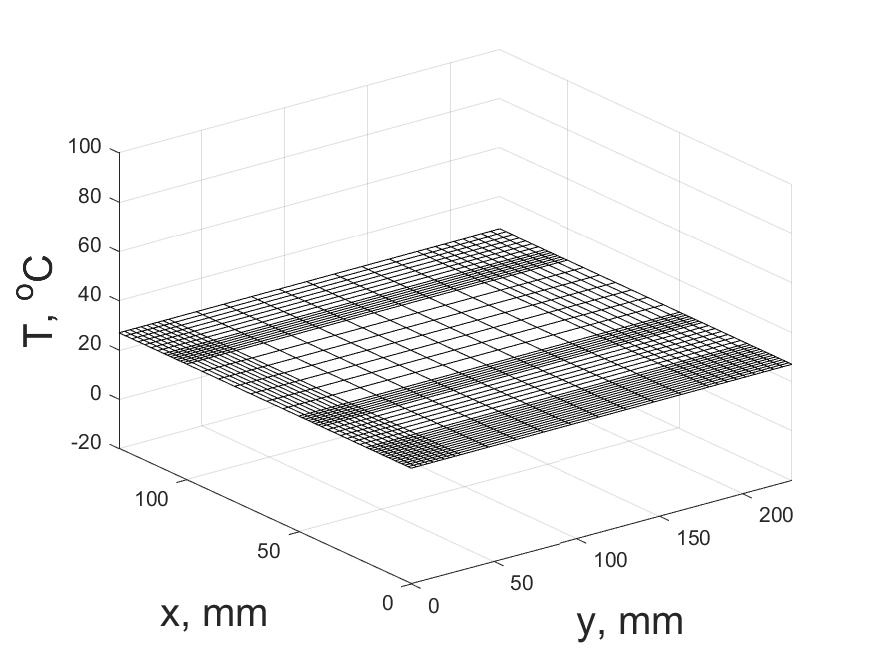
Рис. 2 – Пространственное распределение температуры в неоднородном теле при t = 0 с (неявная схема)

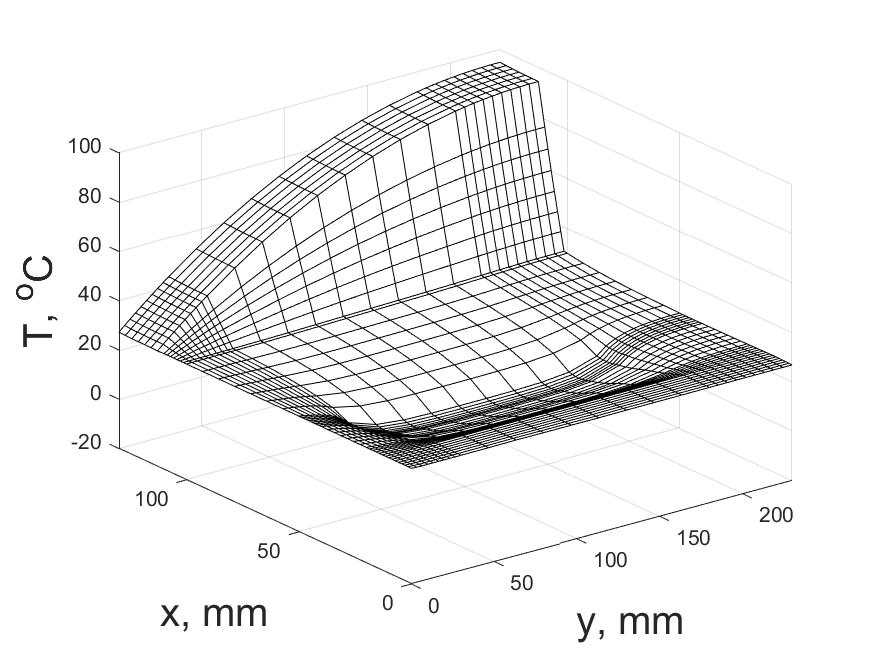
Рис. 3 – Пространственное распределение температуры в неоднородном теле при t = 1,6 с (неявная схема)

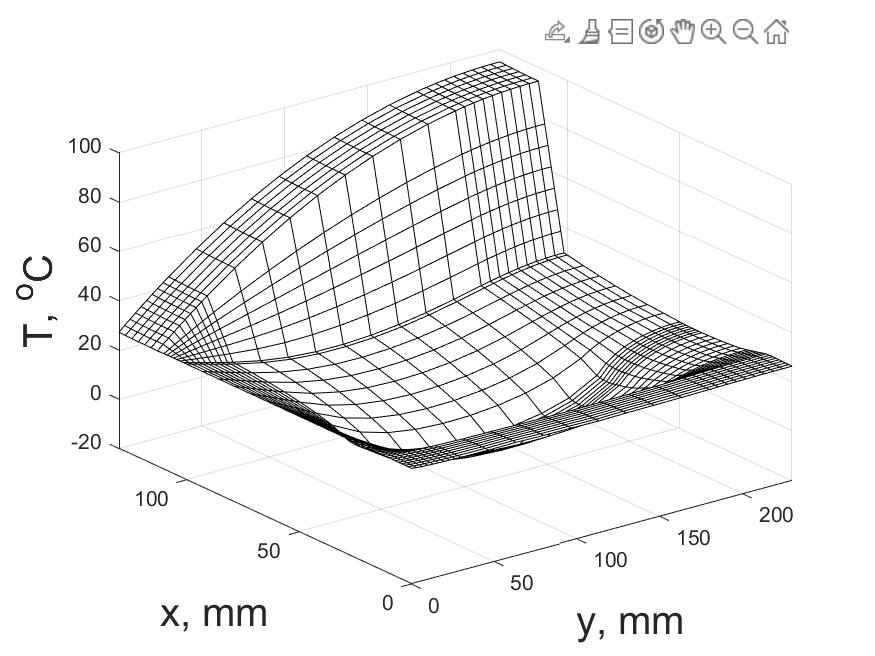
Рис. 4 – Пространственное распределение температуры в неоднородном теле при t = 9,6 с (неявная схема)

Рис. 5 – Пространственное распределение температуры в неоднородном теле при t = 12,8 с (неявная схема)

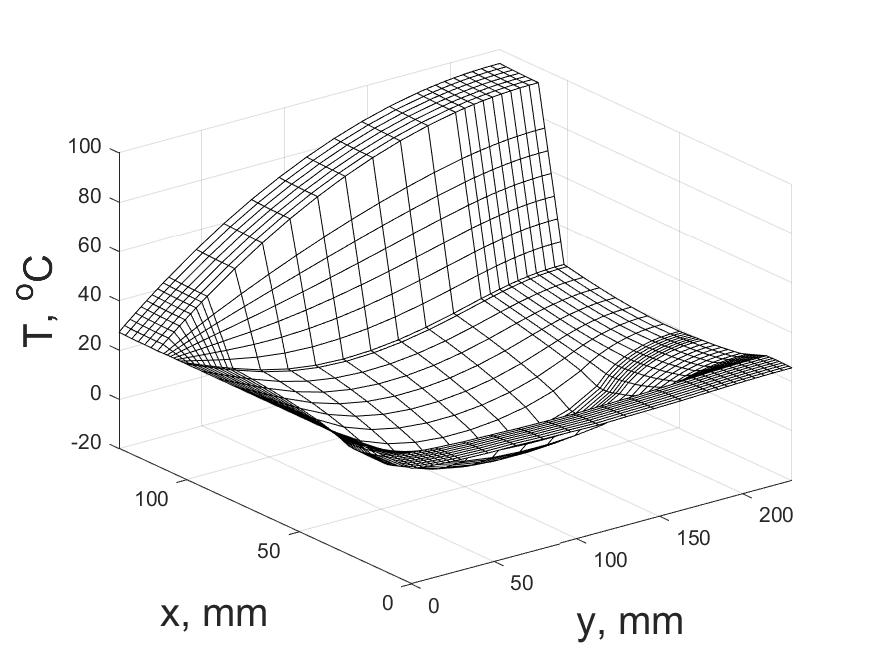
Рис. 6 – Пространственное распределение температуры в неоднородном теле при t = 17,6 с (неявная схема)

Рис. 7 – Пространственное распределение температуры в неоднородном теле при t = 19,2 с (неявная схема)

Вывод: программа в данной работе обеспечивает численное решение уравнения теплопроводности для неоднородного тела с использованием неявной схемы. На каждом временном срезе находятся температуры в точках путём решения СЛАУ.

«+»: по сравнению с явной схемой неявная схема более устойчивая (не нужно подбирать оптимальный шаг по времени), по сравнению с прямым методом последовательный метод по неявной схеме занимает меньший объём оперативной памяти компьютера.