Математика / Ответы / primery_resheny

.

Найдем полный дифференциал от данного выражения:

.

Величины   и   выражают процентные изменения переменных х₁, и х₂, они соответственно равны -0,03 и 0,02. Величина   будет выражать соответствующее процентное изменение переменной  у.

  .

Следовательно, объем товарной продукции не изменился.

Найдем изменение объема товарной продукции в процентном выражении вторым способом. Исходное значение объема товарной продукции в стоимостном выражении было равно    и это составляет 100%. По условию значение х₁ уменьшилось на 3%, т.е. стало 0,97 х₁,  а значение х₂увеличилось на 2%, т.е. стало 1,02х_{2 .} Тогда   Найдем, сколько процентов составляет у_н по отношению к у_исх.

у_исх   -   100%

у_н   -   А %

     .

Так как А = 100 %, то объем товарной продукции не изменился.

2) Производительность труда является отношением объема товарной продукции к фонду заработной платы  . Она была равна   и это составляло 100%. При изменении х₁ и х₂ новая производительность труда будет равна  . Составим пропорцию:

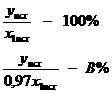
Отсюда

.

Так как В = 103%, то произошло повышение производительности труда на

103% - 100% = 3%.

3) Фондоотдача является отношением объема товарной продукции к стоимости основных фондов  . Она была равна   и это составляло 100%. При изменении х₁ и х₂ новая производительность труда будет равна  . Составим пропорцию:

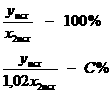
Отсюда

.

Так как С = 98%, то произошло уменьшение фондоотдачи на

100% - 98% = 2%.

Задача 1. Производственная функция фирмы имеет вид:  . Рыночные цены первого и второго ресурсов равны р₁=7, р₂=4. Решить задачу на максимум выпуска фирмы, если ограничения по затратам составляют 28ден.ед.  Составить математическую модель задачи. Задачу решить графически.

Решение. Пусть  - количества первого и второго ресурсов. Затраты на приобретение ресурсов составят  , что не должно превосходить 28. Имеем ограничение по затратам  . Целевая функция максимизируется.  Получена задача математического программирования.

Решим задачу графически.

 

 

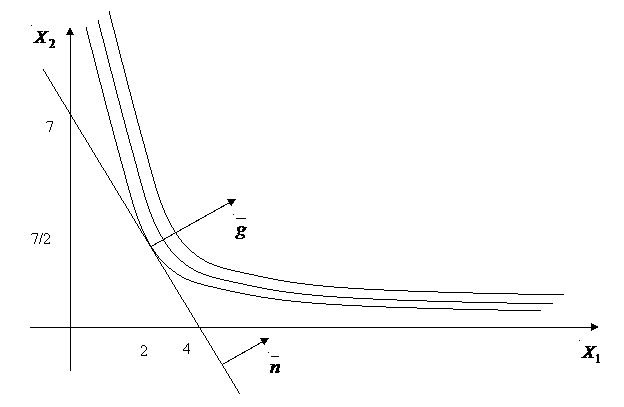
В системе координат   строим прямую   (рис.1) Выбираем полуплоскость, являющуюся областью решений неравенства  . С учетом условий неотрицательностиполучаем, что областью допустимых решений задачи служит треугольник АОВ. Построим линии уровня целевой функции  , которые представляют собой семейство гипербол, расположенных в первой четверти. Находим градиент целевой функции, для чего определяем частные производные:

 или  .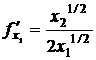

Аналогично  ,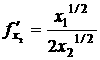

 

получаем вектор градиент целевой функции

,

 

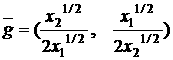который указывает направление роста целевой функции. Наибольшее значение функции в области допустимых решений достигается в точке касания линии уровня и прямой  , где градиент коллинеарен вектору нормали прямой   . Из условия коллинеарностивекторов  получаем:

.

 

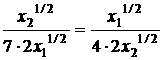Для нахождения координат точки максимума имеем систему уравнений

,

 

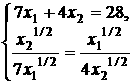решением которой является  , наибольшее значение целевой функции  .

Ответ: наибольший выпуск, равный   , достигается при затратах первого и второго ресурсов в количествах 2 и 7/2 соответственно.

 

 

Задача 2. Найти решение задачи на минимум издержек производства: С=р₁х₁+р₂х₂ при заданном объеме выпуска, если производственная функция фирмы имеет вид: f(x₁,x₂)=x₁^1/4x₂^1/2.  Рыночные цены первого и второго ресурсов равны р₁=3, р₂=7, объем выпуска равен 14ед.  Составить математическую модель задачи. Решить задачу методом Лагранжа.

Решение. Если  - количества первого и второго ресурсов, то суммарные издержки производства составят  . Эта целевая функция задачи минимизируется.  Объем выпуска составляет 14 ед. Следовательно, ограничение по выпуску  принимает вид  . Получена следующая классическая задача оптимизации:

Найти наименьшее значение функции   при ограничении  .

Решим задачу  методом Лагранжа. Составим функцию Лагранжа.

 

Найдем частные производные функции Лагранжа.

,   ,  

 

Приравняем найденные частные производные  нулю и получим систему уравнений для нахождения стационарных точек.

 

 

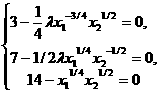
Разделив первое уравнение на второе, получаем соотношение

   

 

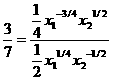
Отсюда получаем   .  Выразив    через   и подставив это соотношение в третье уравнение системы, получим

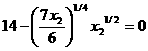,  отсюда   ,  тогда 

 

Издержки при таких затратах ресурсов равны

 

Ответ: минимальные издержки величиной  ед. достигаются  при затратах первого и второго ресурсов в количествах   и  соответственно.