Свойства неопределенного интеграла

 

Теорема 1. Производная от неопределенного интеграларавна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению.

Доказательство. Пусть функция f(x)  имеет первообразнуюF(x), тогда

 f(x)dx = F(x) + c.

Найдем производную и дифференциал от обеих частей равенства.

( f(x)dx)' = (F(x) + c)' = f(x),

d( f(x)dx) = ( f(x)dx)' dx = f(x)dx.

Теорема 2. Интеграл от дифференциала функции равен этой функции с точностью до постоянного слагаемого.

Доказательство.  d f(x) =  f'(x)dx = f(x) + C.

Из теорем 1 и 2 следует, что операции дифференцирования и интегрирования являются взаимнообратными.

Теорема 3. Постоянный множитель можно выносить за знак интеграла.

Доказательство. Пусть функция f(x) имеет первообразнуюF(x).

 f(x)dx = F(x) + C.

Умножим обе части на k .

k  f(x)dx = k F(x) + C₁, где C₁ = k C_.

Найдем производную функции kF(x).

(k F(x))' = k f(x).

Функция k F(x) является первообразной функции k f(x). Следовательно,

 k f(x)dx = k F(x) + C,

 k f(x)dx = k  f(x)dx.

Теорема 4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.

Непосредственное интегрирование

 

Этот вид интегрирования состоит в приведении исходного интеграла к одному или к нескольким табличным с помощью свойств интеграла и тождественных преобразований.

Пример 1.

.

Пример 2. 

.

Метод замены переменной в неопределенном интеграле

 

Теорема 1. Пусть функция х= φ(t) определена идифференцируема на некотором промежутке Т, а Х – множество значений этой функции, на котором определена функция f(x). Тогда, если функция f(x) имеет первообразную на множестве Х, то на множестве Т справедлива формула

 f(x)dx =  f(φ(t))φ'(t)dt.

Доказательство. Найдем дифференциалы обеих частей равенства:

d( f(x)dx) = f(x)dx = f(φ(t))d(φ(t)) = f(φ(t))φ'(t)dt,

d( f(φ(t))φ'(t)dt) = f(φ(t))φ'(t)dt.

Дифференциалы обеих частей равны, значит, сами интегралы могут отличаться лишь на постоянное слагаемое.

При подходящем выборе функции φ(t) интеграл становится значительно проще исходного интеграла.

Пример.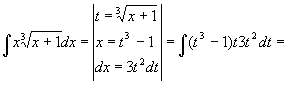 

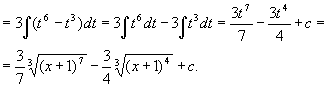
Новую переменную можно не выписывать явно. В таких случаях говорят о введении постоянных и переменных под знак дифференциала или о тождественном преобразовании дифференциала.

Пример 1.   ,

.

Пример 2.   ,

d (sin x) = cos х dx.

Метод интегрирования по частям в неопределенном интеграле

 

Теорема. Пусть функции u и υ определены идифференцируемы на некотором промежутке Т и функция du·υимеет на этом промежутке первообразную. Тогда функция u·dυтакже имеет первообразную на промежутке Т, причем справедлива формула

udυ = uυ - υdu.

Доказательство. Найдем дифференциал от их произведения u · υ.

d(uυ) = du·υ + u·dυ.

Проинтегрируем обе части этого равенства.

d(uυ) = (du·υ + u·d υ).

uυ =  υdu +  udυ,

 udυ = uυ -  υdu  -  формула интегрирования по частям.

С помощью этой формулы первообразная частично находится, и оставшиеся интегральные слагаемые, как правило, - проще исходного интеграла.

Данная формула применяется к интегралам следующих видов.

1)                                          ,

где P(x) - многочлен, его выбирают в качестве u.

2)                                          .

В качестве u  выбирают трансцендентную функцию.

3) Циклические интегралы – это те, в которых подынтегральная функция представляется в виде произведения двух функций, мало меняющихся при интегрировании и дифференцировании.

Пример 1.  

.

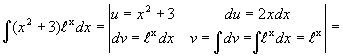
Пример 2.

= .