
- •Теории вероятностей
- •1. Вероятность события. Непосредственный подсчет вероятностей
- •2. Теоремы сложения и умножения вероятностей Теорема сложения вероятностей несовместных событий
- •Теорема умножения вероятностей
- •3. Формула полной вероятности. Формула байеса
- •4. Повторные испытания. Формула бернулли. Асимптотические формулы (пуассона и муавра – лапласа)
- •5. Случайные величины. Способы их задания
- •6. Числовые характеристики случайной величины
- •7. Равномерное распределение
- •8. Показательное распределение
- •9. Нормальное распределение
- •Математической статистике
- •1. Вариационный ряд. Статистические распределения. Эмпирическая функция распределения. Графическое представление статистических распределений
- •2. Выборочные характеристики статистических распределений
- •3. Точечные и интервальные оценки параметров распределения
- •4. Проверка гипотезы о нормальном распределении генеральной совокупности
- •5. Парная линейная корреляционная зависимость. Парный линейный коэффициент корреляции, проверка его значимости. Линейное уравнение регрессии
- •6. Простейшие случаи парной нелинейной корреляционной зависимости. Корреляционное отношение. Нелинейное уравнение регрессии
- •7. Множественный корреляционно-регрессионный анализ
7. Равномерное распределение
Непрерывная
случайная величина X
имеет равномерное
распределение, если плотность
распределения
вероятности постоянна
в интервале (
,![]() ),
а вне его равна нулю, то есть
),
а вне его равна нулю, то есть
![]()
Интегральная функция равномерного распределения имеет вид:
![]()
Графики функций
![]() и F(
и F(![]() )
(рис. 5 и 6) имеют вид:
)
(рис. 5 и 6) имеют вид:

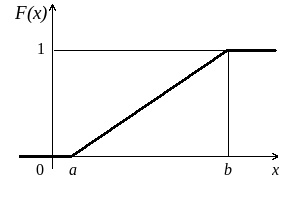
Рис. 5 Рис. 6
Характеристики равномерного распределения:
![]()
Коэффициент
асимметрии
![]() ,
коэффициент эксцесса
,
коэффициент эксцесса
![]() .
.
Вероятность
попадания равномерно распределенной
случайной величины в интервал (![]() ,
,![]() )
(
,
)
находится по формуле:
)
(
,
)
находится по формуле:
![]()
Геометрически эта вероятность представляет собой площадь прямоугольника, заштрихованного на графике функции (рис. 5).
8. Показательное распределение
Непрерывная случайная величина X имеет показательное распределение, если ее плотность распределения вероятности имеет вид:
![]()
где 0 – параметр распределения.
Интегральная функция показательного распределения имеет вид:
![]()
Графики дифференциальной и интегральной функций, соответственно, имеют вид (рис. 9, 10):


Рис.9 Рис.10
Характеристики показательного распределения:
![]()
Коэффициент
асимметрии
![]() ,
коэффициент эксцесса
,
коэффициент эксцесса
![]() .
.
Вероятность
попадания случайной величины в интервал
(, ) (0, )
рассчитывается по формуле:
![]()
9. Нормальное распределение
Непрерывная случайная величина X имеет нормальное распределение, если ее плотность распределения вероятности имеет вид:

где
и
![]() –
параметры
распределения, причем
= M(X),
=
(X).
–
параметры
распределения, причем
= M(X),
=
(X).
График дифференциальной функции распределения называют нормальной кривой, или кривой Гаусса (рис.13).
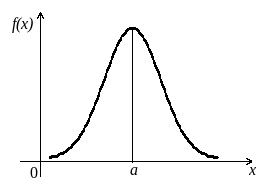
Рис.13
Если
![]() (X)
= 0,
(X)
= 1, то нормально распределенная случайная
величина называется нормированной, ее
дифференциальная функция распределения
(X)
= 0,
(X)
= 1, то нормально распределенная случайная
величина называется нормированной, ее
дифференциальная функция распределения
![]() табулирована.
табулирована.
Вероятность
попадания нормально распределенной
случайной величины в интервал (![]() ,
)
находим по формуле:
,
)
находим по формуле:

Данный интеграл выражается через функцию Лапласа, которую еще называют интегралом вероятностей и обозначают Ф(t):
Ф(t)
 .
.
Функция Лапласа – это вероятность попадания нормированной нормально распределенной случайной величины в интервал ( 0, t).
Функция Лапласа обладает следующими свойствами:
1. Ф(0) = 0.
2. Ф(–t) = –Ф(t), то есть она нечетная.
3. Ф() = 0,5 (практически уже при t 4).
Функция Ф(t) табулирована (см. прил. 2).
Применяя функцию Лапласа, получим:
![]()
При решении задач часто возникает необходимость определения вероятности отклонения нормально распределенной случайной величины от ее математического ожидания:
![]()
ЛЕКЦИИ
ПО
Математической статистике
1. Вариационный ряд. Статистические распределения. Эмпирическая функция распределения. Графическое представление статистических распределений
Полученная в
результате статистического наблюдения
выборка
из n
значений (вариант)
изучаемого количественного признака
X
образует вариационный
ряд.
Ранжированный
вариационный ряд получают, расположив
варианты xj ,
где
![]() ,
в порядке возрастания значений, то есть
,
в порядке возрастания значений, то есть
![]() .
.
Изучаемый признак X может быть дискретным, то есть его значения отличаются на конечную, заранее известную величину (год рождения, тарифный разряд, число людей), или непрерывным, то есть его значения отличаются на сколь угодно малую величину (время, вес, объем, стоимость).
Частотой mi в случае дискретного признака X называют число одинаковых вариант xi , содержащихся в выборке. В ранжированном вариационном ряду одинаковые варианты очевидно расположены подряд:

Вариационный ряд
для дискретного
признака X
принято наглядно и компактно представлять
в виде таблицы, в первой строке которой
указаны k
различных значений xi
изучаемого признака, а во второй строке
– соответствующие этим значениям
частоты mi ,
где
![]() .
Такую таблицу называют статистическим
(выборочным) распределением.
.
Такую таблицу называют статистическим
(выборочным) распределением.
Переход от исходного вариационного ряда дискретного признака X к соответствующему статистическому распределению поясним на простом примере:
вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем) – 7, 17, 14, 17, 10, 7, 7, 14, 7, 14;
ранжированный вариационный ряд –
xj :
![]() ,
где
,
где
![]() ,
n
= 10;
,
n
= 10;
соответствующее статистическое распределение (
 ,
k
= 4):
,
k
= 4):
xi |
7 |
10 |
14 |
17 |
mi |
4 |
1 |
3 |
2. |
Статистическое распределение для непрерывного признака X принято представлять интервальным рядом – таблицей, в первой строке которой указаны k интервалов значений изучаемого признака X вида (xi–1 – xi ), а во второй строке – соответствующие этим интервалам частоты mi , где . Обозначение (xi–1 – xi ) – указывает не разности, а все значения признака X от xi–1 до xi , кроме правой границы интервала xi .
Для непрерывного признака X частота mi – число различных xj , попавших в соответствующий интервал: xj[xi–1 ; xi ):
x3
xn
xn–1
xj+1
xj+2
xj
x4
x1
x2
xj
:



X
xk
xk–1
xi
xi–1
x1
mk
=
2
mi
=
3
m1
=
4
x0
Переход от исходного вариационного ряда непрерывного признака X к соответствующему статистическому распределению поясним на простом примере:
вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем) –3,14; 1,41; 2,87; 3,62; 2,71; 3,95;
ранжированный вариационный ряд – xj : 1,41; 2,71; 2,87; 3,14; 3,62; 3,95; где , n = 6;
соответствующее статистическое распределение ( , k = 3):
xi |
1–2 |
2–3 |
3–4 |
mi |
1 |
2 |
3. |
Если число различных значений дискретного признака очень велико, то для удобства дальнейших вычислений и наглядности статистическое распределение такого дискретного признака также может быть представлено в виде интервального ряда.
Вместо частот mi
во второй строке могут быть указаны
относительные
частоты
![]() (частости).
Очевидно, что сумма частот равна объему
выборки (выборочной совокупности) n
, а сумма относительных частот (частостей)
равна единице:
(частости).
Очевидно, что сумма частот равна объему
выборки (выборочной совокупности) n
, а сумма относительных частот (частостей)
равна единице:
![]()
![]() .
.
Далее показаны четыре возможных формы представления статистических распределений с соответствующими краткими названиями:
-
Дискретный ряд частот
Интервальный ряд частот
xi
x1
x2
…
xk
xi–1–xi
x0–x1
x1–x2
…
xk–1–xk
mi
m1
m2
mk ,
mi
m1
m2
…
mk ,
Дискретный ряд частостей
Интервальный ряд частостей
xi
x1
x2
…
xk
xi–1–xi
x0–x1
x1–x2
…
xk–1–xk
wi
w1
w2
wk ,
wi
w1
w2
…
wk .
Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд распределения называют кумулятивным.
Накопленной частотой называется число значений признака Х, меньших заданного значения x : H(x) = m(Х x), то есть, число вариант xj в выборке, отвечающих условию xj < x.
Переход от дискретного ряда частот к кумулятивному ряду – дискретному ряду накопленных частот задается соотношениями:
![]()
или в табличной форме:
xi |
x1 |
x2 |
x3 |
… |
xi |
… |
xk |
xk+1 |
H(xi) |
0 |
m1 |
m1+m2 |
… |
H(xi–1) + mi–1 |
… |
H(xk–1) + mk–1 |
H(xk) + mk= n. |
Переход от интервального ряда частот к кумулятивному ряду – интервальному ряду накопленных частот задается соотношениями:
![]()
или в табличной форме:
xi–1–xi |
––x0 |
x0–x1 |
x1–x2 |
… |
xi–1–xi |
… |
xk–1–xk |
H(xi) |
0 |
m1 |
m1+m2 |
… |
H(xi–1) + mi |
… |
H(xk–1) + mk= n. |
Накопленной
относительной частотой
(накопленной
частостью)
называется отношение числа значений
признака Х,
меньших заданного значения x
, к объему выборки n :
![]() , то есть, доля вариант xj
в выборке, отвечающих условию xj < x.
, то есть, доля вариант xj
в выборке, отвечающих условию xj < x.
По аналогии с
теоретической
функцией
распределения генеральной совокупности
![]() ,
которая определяет вероятность
события
Х
:
= P(Х
),
вводят понятие эмпирической
функции распределения
,
которая определяет вероятность
события
Х
:
= P(Х
),
вводят понятие эмпирической
функции распределения
![]() ,
которая определяет относительную
частоту
этого же события
Х
,
то есть
=
,
которая определяет относительную
частоту
этого же события
Х
,
то есть
=
![]() .
Таким образом, эмпирическая
функция распределения
задается рядом накопленных
относительных частот.
.
Таким образом, эмпирическая
функция распределения
задается рядом накопленных
относительных частот.
Из теоремы Бернулли следует, что стремится по вероятности к F(x):
![]()
поэтому эмпирическую функцию распределения можно использовать для оценки теоретической функции распределения генеральной совокупности.
Дискретный ряд накопленных относительных частот может быть получен двумя равноправными способами:
1) переход от дискретного ряда частостей к кумулятивному ряду – дискретному ряду накопленных частостей задается соотношениями:
![]()
или в табличной форме:
xi |
x1 |
x2 |
x3 |
… |
xi |
… |
xk |
xk+1 |
|
0 |
w1 |
w1+w2 |
… |
(xi–1) + wi–1 |
… |
(xk–1) + wk–1 |
(xk) + wk= 1; |
2) переход от дискретного ряда накопленных частот к дискретному ряду накопленных частостей задается соотношением:
![]()
Интервальный ряд накопленных относительных частот может быть получен двумя равноправными способами:
1) переход от интервального ряда частостей к кумулятивному ряду – интервальному ряду накопленных частостей задается соотношениями:
![]()
или в табличной форме:
xi–1–xi |
––x0 |
x0–x1 |
x1–x2 |
… |
xi–1–xi |
… |
xk–1–xk |
(xi) |
0 |
w1 |
w1+w2 |
… |
(xi–1) + wi |
… |
(xk–1) + wk= 1; |
2) переход от интервального ряда накопленных частот к интервальному ряду накопленных частостей задается соотношением:
![]()
Для наглядности принято использовать следующие формы графического представления статистических распределений:
дискретный ряд изображают в виде полигона. Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами ( i , i); аналогично, полигон относительных частот – ломаная, отрезки которой соединяют точки с координатами ( , wi );
интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых – интервалы длиной
 ,
а высоты – плотности частот
,
а высоты – плотности частот
 .
В случае гистограммы
относительных частот
высоты прямоугольников – плотности
относительных частот
.
В случае гистограммы
относительных частот
высоты прямоугольников – плотности
относительных частот
 .
Здесь в общем случае
.
Здесь в общем случае
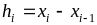 ,
однако на практике чаще всего полагают
величину h
одинаковой для всех интервалов:
,
однако на практике чаще всего полагают
величину h
одинаковой для всех интервалов:
 .
Очевидно для ранжированного вариационного
ряда
.
Очевидно для ранжированного вариационного
ряда
 ;
;
 .
В скобках указаны индексы j
исходного
ранжированного вариационного ряда.
.
В скобках указаны индексы j
исходного
ранжированного вариационного ряда.
Площадь гистограммы есть сумма площадей ее прямоугольников:
![]()
![]()
таким образом,
площадь гистограммы частот
![]() равна объему выборки, а площадь гистограммы
относительных частот
равна объему выборки, а площадь гистограммы
относительных частот
![]() равна единице.
равна единице.
В теории вероятностей
гистограмме относительных частот
соответствует график плотности
распределения вероятностей
![]() .
Поэтому гистограмму можно использовать
для подбора закона распределения
генеральной совокупности;
.
Поэтому гистограмму можно использовать
для подбора закона распределения
генеральной совокупности;
кумулятивные ряды графически изображают в виде кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат – накопленные частоты Н( ) или относительные накопленные частоты , а затем точки с координатами ( i ; H( i )) или ( i ;
 )
соединяют отрезками прямой. В теории
вероятностей кумуляте соответствует
график интегральной функции распределения
.
)
соединяют отрезками прямой. В теории
вероятностей кумуляте соответствует
график интегральной функции распределения
.
Замечание 1. Если в статистическом исследовании исходным является статистическое распределение в виде интервального ряда (сгруппированные данные), а исходный вариационный ряд недоступен, то точное расположение отдельных вариант, попавших в каждый из интервалов неизвестно. Только выбирая в качестве аргумента эмпирической функции распределения правую границу интервала (xi–1–xi), мы уверены, что все варианты, попавшие в этот интервал, будут учтены (просуммированы) в значении накопленной частоты (накопленной относительной частоты), соответствующей этому интервалу.
Поэтому в случае интервального ряда значения и H(x) точно определены лишь для правой границы интервала: x = xi . В остальных точках интервала xi–1 < x xi значения и H(x) можно задать лишь приближенно. Примером может служить кумулята, отрезки прямых которой представляют собой выраженную в графической форме линейную интерполяцию значений и H(x) на интервале xi–1 < x xi .
Замечание 2.
В случае дискретного ряда использовать
кумуляту для изображения
и H(x)
можно лишь условно, для наглядности.
Более корректным является изображение
эмпирической функции распределения
(а также H(x))
по аналогии с теоретической функцией
распределения
![]() дискретной случайной величины (см. рис.
2) ступенчатым графиком – отрезками
прямых, параллельных оси абсцисс; длины
отрезков – hi
= xi
– xi–1
, расстояния
от отрезков до оси абсцисс –
дискретной случайной величины (см. рис.
2) ступенчатым графиком – отрезками
прямых, параллельных оси абсцисс; длины
отрезков – hi
= xi
– xi–1
, расстояния
от отрезков до оси абсцисс –
![]() (или H(xi)).
(или H(xi)).
