
- •1.Определение срока службы приводного устройства
- •2.Выбор двигателя. Кинематический расчет привода
- •3.Выбор материала зубчатых передач. Определение допускаемых напряжений.
- •4.Расчет закрытой цилиндрической передачи.
- •4.1 Проектный расчет.
- •4.2. Проверочный расчет
- •5. Расчёт открытой цилиндрической зубчатой передачи
- •5.1. Выбор материала зубчатых передач. Определение допускаемых напряжений.
- •5.2 Проектный расчет.
- •5.3. Проверочный расчет
4.1 Проектный расчет.
1.Межосевое расстояние определяется по формуле:
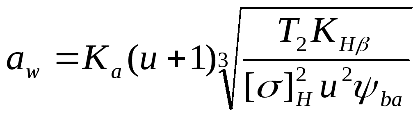 ,
где
,
где
Ка = 43– вспомогательный коэффициент для косозубых передач; ψb = 0,28 – коэффициент ширины венца колеса; КНβ = 1,0 – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся колес; u – передаточное число редуктора.
aw=
43*(5+1) = 72,25 (мм)
= 72,25 (мм)
Округлим до стандартного значения aw = 73 (мм).
2. Определим модуль зацепления m по формуле:
m
=
 ,
где
,
где
Кm=
5,8 – вспомогательный коэффициент; b2
=
ψ*aw
– ширина венца колеса, мм; d2
=
 – делительный диаметр колеса, мм.
– делительный диаметр колеса, мм.
Расчет:
m
=
 0,85
0,85
Полученное значение модуля m округлим в большую сторону до стандартного числа m = 1
3. Определим угол наклона зубьев для косозубых передач:
 min
min
 =
=
 º
º
4. Определим суммарное число зубьев шестерни и колеса:
 z1
+z2
=
z1
+z2
=
 =
=
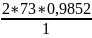 = 143,84
= 143,84
Полученное значение округлим в меньшую сторону до целого числа: 143
Уточним действительную величину угла наклона зубьев:
ᵦ )
= arccos(
)
= arccos(
5. Определим число зубьев шестерни:
z1
Примем 24
6. Найдем число зубьев колеса:
z2
=
 z1
=143
– 24 = 119
z1
=143
– 24 = 119
7. Фактическое передаточное число uф и отклонение Δu от заданного u:
uф=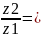
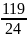 =4,96
;
=4,96
;
Δu
=
 =
=
 *
100% = 0,83% < 4%
*
100% = 0,83% < 4%
Норма отклонения передаточного числа Δu выполняется.
8. Фактическое межосевое расстояние:
aw
=
 =
=
 =
73 (мм)
=
73 (мм)
9. Фактические основные геометрические параметры передачи, мм.
Таблица 4.1
Параметр |
Шестерня |
Колесо |
|
косозубая |
косозубая |
||
Диаметр |
делительный |
d1=m*z1/cos d1= 24,5 |
d2=m*z2/cos d2 = 121,5 |
вершин зубьев |
da1 = d1+2*m da1= 26,5 |
da2=d2+2*m da2= 123,5 |
|
впадин зубьев |
df1= d1-2.4*m df1= 22,1 |
df2= d2-2.4*m df2= 119,1 |
|
Ширина венца |
b1=b2+2 b1 = 22 |
b2=ψa*aw b2 =20,44 = 20 |
|
4.2. Проверочный расчет
1. Проверка межосевого расстояния:
aw= =
=
2. Проверка контактного напряжения σН, Н/мм:
σН
=
К* ≤ [σ]Н,
где
≤ [σ]Н,
где
К-
вспомогательный коэффициент, К = 376; Ft
=
 – окружная сила в зацеплении, Н;
– окружная сила в зацеплении, Н;
 коэффициент, учитывающий распределение
нагрузки между зубьями;
коэффициент, учитывающий распределение
нагрузки между зубьями;
 коэффициент динамической нагрузки,
зависящей от степени нагрузки и степени
точности передачи.
коэффициент динамической нагрузки,
зависящей от степени нагрузки и степени
точности передачи.
Расчет:
σН
=
376* = 420,42
= 420,42
420,42>414, перегрузка 1,55% допускается
3. Проверка напряжения изгиба зубьев шестерни [σ]F1 и колеса [σ]F2, Н/мм²:
σF2
= Y
F2*Yᵦ* KFα
*KFᵦ*KFv
≤
[σ]F2
KFα
*KFᵦ*KFv
≤
[σ]F2
σF1
= σF2* ≤
[σ]F1
, где
≤
[σ]F1
, где
KFα
= 1 – коэффициент учитывающий распределение
нагрузки между зубьями; KFᵦ
=
1 – коэффициент неравномерности нагрузки
по длине зуба; KFv
= 1.11 – коэффициент динамической нагрузки,
зависящей от окружной скорости колес
(3,2) и степени точности передачи (9); Y
F2
и Y
F1
–
коэффициенты формы зуба шестерни и
колеса; Yᵦ=1
-
 - коэффициент, учитывающий наклон зуба.
- коэффициент, учитывающий наклон зуба.
Расчет:
σF2
= 3.6*(1 -
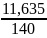 )*
)* 1
·1·1.11
= 79,46
≤
[σ]F2
=
145
1
·1·1.11
= 79,46
≤
[σ]F2
=
145
σF1
= 79,46* = 86,08 ≤ [σ]F1
=
191
= 86,08 ≤ [σ]F1
=
191
4.Все результаты вычислений занесем в таблицу
Табличный ответ к разделу 4 Таблица 4.2
Проектный расчет |
||||||
Параметр |
Значение |
Параметр |
Значение |
|||
Межосевое расстояние aw |
73 |
Угол наклона зубьев β |
11,635° |
|||
Модуль зацепления |
1 |
Диаметр делительной окружности: шестерни d1 колеса d2 |
24,5 121,5 |
|||
Ширина зубчатого венца: Шестерни b1 Колеса b2 |
22 20 |
|||||
Число зубьев: шестерни z1 колеса z2 |
24 119 |
Диаметр окружности вершин: шестерни da1 колеса da2
|
26,5 123,5 |
|||
Вид зубьев |
косозубые |
Диаметр окружности впадин: Шестерни df1 Колеса df2 |
22,1 119.1 |
|||
Проверочный расчет |
||||||
Параметр |
Допускаемые значения |
Расчетные значения |
||||
Контактные напряжения σ, Н/мм² |
414 |
420,42 |
||||
Напряжения изгиба, Н/мм² |
σF1 |
191 |
86,08 |
|||
σF2 |
145 |
79,46 |
||||
