
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •Глава II. Практическое применение икт при изучении линий второго порядка
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Линии второго порядка в элементарной математике
- •Вывод уравнения окружности
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Изображение окружности
- •Вывод уравнения эллипса
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •Вывод уравнения гиперболы
- •Исследование свойств гиперболы по ее уравнению
- •1) Пересечение гиперболы с осями координат:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Вывод уравнения параболы
- •Исследование свойств параболы
- •Линии второго порядка в элементарной математике
- •Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
- •Глава II. Практическое применение икт при изучении линий второго порядка
1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
Обязательной и неотъемлемой частью учебного процесса, а также изучения линий второго порядка является тематическое планирование и учебники. Рассматривая данные линии, возник такой вопрос: «А как же линии второго порядка изучаются в школьном курсе алгебры 7-9 классов». Для того чтобы ответить на этот вопрос стало необходимым проанализировать комплекты учебников по алгебре 7-9 классов таких авторов, как: А.Г. Мордкович, Ш. А. Алимов и Г.В. Дорофеев. ( Таблица №2)
Таблица № 2
|
Линии второго порядка |
Алгебра, автор А. Г. Мордкович |
Алгебра, автор Ш. А. Алимов, Ю. М. Колягин. |
«Математика: арифметика. Алгебра. Анализ данных», автор Г. В. Дорофеев, С. Б. Суворова. | ||||||||||
|
Функция
|
Изучение
функции начинается в 7 классе с § 37,
где переход от линейной функции к
квадратичной осуществляется на
примере. (пусть x
– сторона квадрата, y
– его площадь, то
Вводится понятие таблица значений, а затем полученные координаты строятся в прямоугольной системе координат. И сразу же говорится, что построенная линия называется параболой. Далее перечисляются геометрические свойства параболы:
Построение
функции
Весь материал представлен параллельно с примерами и изображенными графиками функций.
|
В
8 классе в §35на
примере тела, брошенного вверх со
скоростью v,
выводится формула
Начиная
с §36 , рассматривается функция
В конце параграфа представлена система заданий на усвоение и закрепление материала. Такие задания, как:
|
Упражнения к разделены на уровни А и Б и представлены в широком диапазоне сложности. В конце главы содержатся задания для самопроверки, указывающие обязательный уровень подготовки ученика. Одновременно каждая глава содержит дополнительный материал, позволяющий учащимся выйти за рамки круга обязательных вопросов, углубить знания, познакомиться с новыми приемами решения задач (рубрики «Для тех, кому интересно», «Дополнительные задания к главе»). | ||||||||||
|
Функция
|
Данная
функция рассматривается в 8
классе в 3-ей главе § 17. И здесь говориться
о том, что функция
И при a<0 с непосредственной опорой на геометрическую модель-параболу. После теоретической части идут непосредственно, задания на усвоение:
1)
Найти наиб. И наим. Значения функции
2)
Решить уравнение
Задания на закрепление, охватывают всю теоретическую часть и представлены в большом количестве. Здесь приведены задания на построение функции как в явной форме, так и построение линии по заданным значениям, свойствам. Также имеются задания на исследование уже построенных функций по рисункам. |
Функция
рассматривается в 8 классе в § 37.
Изучение сразу начинается с построения
графика функции
Затем задается задача. На
одной координатной плоскости построить
графики функций Упражнения представлены в конце параграфа и содержат как легкие, так и повышенной сложности задания. |
| ||||||||||
|
Функция
|
Данная
функция и её свойства изучаются в 8
классе § 37. Изучение начинается с
рассмотрения многочлена
При
этом дается задание: Не выполняя
построения графика функции
После
построения графика данной функции
вводится алгоритм построения параболы
Практическая часть содержит большой объем заданий: легких, средней сложности и повышенной сложности. |
Изучение данного графика функции начинается с §38, где сразу дается задание:
Построить
график функции
Практическая часть разделена на уровни по сложности, каждый из уровней имеет по 6 заданий. Некоторые из них:
|
| ||||||||||
|
Функция
|
В
8 классе в § 18 поясняется, что познакомимся
с функцией
Затем
дается пример: Найти наименьшее и
наибольшее значение функции
Далее
вводится определение графика функции
И поясняется, что две величины x и y обратно пропорциональны, если они связаны отношением xy=k (где k – число, отличное от нуля)
Дальше
автор по отдельности выделяет свойства
функции
Практическая часть для закрепления и усвоения данного материала содержит большое количество заданий трех уровней сложности. При этом это задачи как на построение графика функции, так и на исследование его свойств по строящимся чертежам, так и по готовым рисункам. |
Функция
изучается в 9 классе, начиная с §15.
Изучение начинается с задания: Построить
график функции
(-∞;0)˅(0;+∞);
2)
нечетная, так как
3) убывает на промежутке x>0; 4) При x>0 функция принимает положительные значения;
Затем
говорится, что график функции
Сразу
дается на рассмотрение задача
2:
Построить график функции
Исследуя две функции поясняется, что функции симметричны относительно оси абсцисс.
Функция
Далее следует практическая часть, состоящая по сложности из уровней. Каждый из уровней содержат по четыре задачи на закрепление.
|
Функция изучается с §22 по §23. В §22 на рассмотрение выносится две задачи:
В
первой задаче, если скорость обозначить
за v,
тогда
если k>0, то ветви расположены в I и III координатных четвертях; а если k<0, то во II и IV координатных четвертях.
После
выделенных свойств, говорится, что
кривые вида
На этом теоретическая часть заканчивается, и начинается практическая часть, состоящая из двух уровней сложности, по количеству заданий и их характеру для изучаемой темы возможно достаточно хорошо усвоить и закрепить материал, так как все задания различны. |
Выполняя сравнительный анализ учебников можно сделать вывод, что в учебниках А. Г. Мордковича теоретический материал достаточно интересно, изучение нового материала идет с опорой на изученный материал, и начинается непосредственно с рассмотрения конкретного примера или задачи, которые в свою очередь в ходе решения приводят к той или иной функции. Следует отметить, что для изучения каждой из функции Мордкович придерживается определенного порядка:
Приводится пример или рассматривается задача, приводящая к виду квадратичной функции;
При конкретном значении коэффициента для функции составляется таблица значений и строится график функции;
По графику функции выполняется исследование свойств.
Причем в промежутках, для каждого из перечисленных пунктов приводятся примеры с решением для возможного самостоятельного изучения темы. Таким образом, теоретический материал изучаемой темы в каждом из трех учебников содержит по 3-4 примера. В отличие от учебников других рассматриваемых авторов, в учебниках А. Г. Мордковича теоретический материал сопровождается большим количеством наглядности (рисунков).
Что касается системы задач, то в учебном комплекте она разделена на 2 уровня по сложности. Первый, из которых обозначается пустым кружочком и содержит задания на применение изученных свойств или алгоритма, а второй закрашенным, требующим мыслить.
При сравнении практической части данного комплекта учебников с комплектом учебников Алимова, можно сделать вывод, что у Шавката Арифджановича практическая часть очень мала по своему содержанию, так как для каждого параграфа приведено всего по 4-5 заданий для каждого уровня.
Рассматривая комплект учебников по алгебре 7-9 классов под редакцией Г. В. Дорофеева, можно сказать, что содержащаяся для каждого параграфа практическая часть разделена на две части по уровню сложности. Первую часть обозначают буквой А и в неё помещены упражнения, требующие от учеников о основном умения решать по алгоритму. А во вторую часть, обозначаемой буквой В, включены упражнения, при решении которых требуется умение мыслить и анализировать. В основном в каждой части В (в конце) содержится задача - исследование. При этом формулировки упражнений интересны, разнообразны, и местами прослеживается непосредственная связь с другими предметами (физика, геометрия). Учебники содержат не только разнообразные упражнения, но и дополнительный материал в рублике «Для тех, кому интересно», «Вопросы для повторения», Задачи для самопроверки»


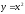 ).
Затем независимой переменнойx
дают конкретные значения, чтобы
рассчитать значения y
и вводится таблица вида:
).
Затем независимой переменнойx
дают конкретные значения, чтобы
рассчитать значения y
и вводится таблица вида:  и
и ,
сравнивание, и анализ графика.
,
сравнивание, и анализ графика. ,
и дается определение квадратичной
функции.
,
и дается определение квадратичной
функции.  приa=1,b=c=0.
Составляется таблица значений, строятся
точки, кривую называют параболой.
Сразу рассматриваются её свойства:
приa=1,b=c=0.
Составляется таблица значений, строятся
точки, кривую называют параболой.
Сразу рассматриваются её свойства: ,
найти значениеy
при
,
найти значениеy
при
 и т.д.;
и т.д.; больше
9, меньше 16?
больше
9, меньше 16? и прямой
и прямой

 аналогична
функции
аналогична
функции
 приa=1.
Затем рассматриваются функции
приa=1.
Затем рассматриваются функции
 и
и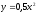 ,
составляется таблица значений, строятся
графики (наглядность построения) и
сравниваются. Затем идет пояснение,
что каждая линия- парабола, а осьy
–ось симметрии. Далее рассматривается
случай при a=-1,
выполняется построение графика, и
делается вывод о направлении ветвей
параболы. После чего дается определение
функции
,
составляется таблица значений, строятся
графики (наглядность построения) и
сравниваются. Затем идет пояснение,
что каждая линия- парабола, а осьy
–ось симметрии. Далее рассматривается
случай при a=-1,
выполняется построение графика, и
делается вывод о направлении ветвей
параболы. После чего дается определение
функции
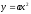 .
Отдельным пунктом автор выделяет
свойства
.
Отдельным пунктом автор выделяет
свойства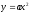 приa>0:
приa>0: возрастает
при x≥0
и убывает при x≤0.
возрастает
при x≥0
и убывает при x≤0. ограничена
снизу, не ограничена сверху.
ограничена
снизу, не ограничена сверху. -
луч[0;+∞)
-
луч[0;+∞) на
отрезках: [0;2],[-2;-1],[-1;1,5].
на
отрезках: [0;2],[-2;-1],[-1;1,5]. .
и другие.
.
и другие.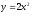 и
и
 с
помощью таблицы значений. Сравнивая
графики, делается вывод о том, что
каждую точку графика функции
с
помощью таблицы значений. Сравнивая
графики, делается вывод о том, что
каждую точку графика функции можно
получить из точки графика функции
можно
получить из точки графика функции с
той же абсциссой увеличением её
ординаты в 2 раза. Далее дается
определение функции
с
той же абсциссой увеличением её
ординаты в 2 раза. Далее дается
определение функции и
перечисляются свойства при a≠0:
и
перечисляются свойства при a≠0: принимает
положительные значения, еслиa<0-отрицательные.
И если значение функции
принимает
положительные значения, еслиa<0-отрицательные.
И если значение функции
 равно
0, значитx=0.
равно
0, значитx=0.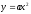 возрастает
приx≥0
и убывает при x≤0;если
a<0,
то функция
возрастает
приx≥0
и убывает при x≤0;если
a<0,
то функция
 убывает приx≥0
и возрастает при x≤0.
убывает приx≥0
и возрастает при x≤0. и
и .
С помощью этих графиков решить
неравенство
.
С помощью этих графиков решить
неравенство .
.
 ,
гдеa,b,c-числа,
причем a≠0.
И поясняется, что это квадратичный
трехчлен. Затем рассматривается
функция
,
гдеa,b,c-числа,
причем a≠0.
И поясняется, что это квадратичный
трехчлен. Затем рассматривается
функция
 и
дается ее определение. При этом
рассматривается несколько функций:
и
дается ее определение. При этом
рассматривается несколько функций: и делается обобщение, что эти функции
являются квадратичными. Автор предлагает
рассмотреть квадратный трехчлен
и делается обобщение, что эти функции
являются квадратичными. Автор предлагает
рассмотреть квадратный трехчлен и путем преобразований привести его
к виду
и путем преобразований привести его
к виду
 ,
где
,
где
 .
Затем вводится формула
.
Затем вводится формула и поясняется, что это формула для
вычисления вершины параболы.
и поясняется, что это формула для
вычисления вершины параболы.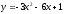 ,
ответить на следующие вопросы:
,
ответить на следующие вопросы: .
. и
сравнить его с графиком функции
и
сравнить его с графиком функции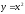 .
После проведенных рассуждений делается
заключение, что графиком функции
.
После проведенных рассуждений делается
заключение, что графиком функции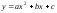 является парабола, полученная сдвигом
параболы
является парабола, полученная сдвигом
параболы вдоль координатных осей. И перечисляются
свойства:
вдоль координатных осей. И перечисляются
свойства: ,
где
,
где ;
; .
. .
.
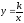 ,
где коэффициентk
может принимать любые значения, кроме
k=0.
И предлагается рассмотреть функцию
при k=1,
составляется таблица значений при
x>0,
и строится график функции
,
где коэффициентk
может принимать любые значения, кроме
k=0.
И предлагается рассмотреть функцию
при k=1,
составляется таблица значений при
x>0,
и строится график функции
 ,
а затем приx<0.
Дальше говориться, что этот график
функции
,
а затем приx<0.
Дальше говориться, что этот график
функции
 называется гиперболой. По чертежу
перечисляются основные свойства:
называется гиперболой. По чертежу
перечисляются основные свойства: :
на отрезке [1/2;4], на полуинтервале
[-8;-1] и подробно расписывается ход
действий.
:
на отрезке [1/2;4], на полуинтервале
[-8;-1] и подробно расписывается ход
действий. .
. при k>0 и приk<0.
Для усвоения изученного материала
предлагается решить уравнение
при k>0 и приk<0.
Для усвоения изученного материала
предлагается решить уравнение
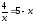 .
. .
И по графику начинается изучение
свойств:
.
И по графику начинается изучение
свойств: при
при .
.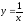 называется
гиперболой, а две части, из которых
она состоит, называются ветвями
гиперболы.
называется
гиперболой, а две части, из которых
она состоит, называются ветвями
гиперболы. приk=2
и k=-2.
приk=2
и k=-2. соотносится с функцией
соотносится с функцией и говорится, что
и говорится, что обладает теми же свойствами, что и
обладает теми же свойствами, что и .
. при
k>0
выражает обратную пропорциональную
зависимость между x
и y.
И приводится пример из физики.
при
k>0
выражает обратную пропорциональную
зависимость между x
и y.
И приводится пример из физики. .
А во второй задаче, если обозначить
высоту заh,
получим:
.
А во второй задаче, если обозначить
высоту заh,
получим:
 .
Обобщая эти задачи, говорится, что
функции в каждой из них получаются
делением некоторого отличного от нуля
числа на соответствующее значение
аргумента. Обозначив число буквойk,
а аргумент и функцию соответственно
x
и y
получаем общий вид формул:
.
Обобщая эти задачи, говорится, что
функции в каждой из них получаются
делением некоторого отличного от нуля
числа на соответствующее значение
аргумента. Обозначив число буквойk,
а аргумент и функцию соответственно
x
и y
получаем общий вид формул:
 ,
гдеk-
число, отличное от нуля. После чего
рассматривается пропорция
,
гдеk-
число, отличное от нуля. После чего
рассматривается пропорция
 ,
говорится, что частное двух значений
переменнойx
обратно частному соответствующих им
значений переменной y.
И такие переменные называют обратно
пропорциональными. К данному параграфу
прилагаются практические задания по
уровню сложности на составление
пропорции, на нахождение одного из
компонентов формулы
,
говорится, что частное двух значений
переменнойx
обратно частному соответствующих им
значений переменной y.
И такие переменные называют обратно
пропорциональными. К данному параграфу
прилагаются практические задания по
уровню сложности на составление
пропорции, на нахождение одного из
компонентов формулы
 .
В §23 рассматривается график функции
.
В §23 рассматривается график функции приk=12.
Составляется таблица значений для
положительными абсциссами, а затем с
отрицательными и выполняется построение.
Анализируя построенные графики
функции, выделяются следующие свойства:
приk=12.
Составляется таблица значений для
положительными абсциссами, а затем с
отрицательными и выполняется построение.
Анализируя построенные графики
функции, выделяются следующие свойства: расположены симметрично относительно
начала координат:
расположены симметрично относительно
начала координат: называются гиперболами.
называются гиперболами.