
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •Глава II. Практическое применение икт при изучении линий второго порядка
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Линии второго порядка в элементарной математике
- •Вывод уравнения окружности
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Изображение окружности
- •Вывод уравнения эллипса
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •Вывод уравнения гиперболы
- •Исследование свойств гиперболы по ее уравнению
- •1) Пересечение гиперболы с осями координат:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Вывод уравнения параболы
- •Исследование свойств параболы
- •Линии второго порядка в элементарной математике
- •Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
- •Глава II. Практическое применение икт при изучении линий второго порядка
Вывод уравнения параболы
Введем
прямоугольную систему координат, где
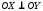 .
Пусть ось
.
Пусть ось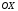 проходит через фокусF
параболы
и перпендикулярен директрисе, а ось
проходит через фокусF
параболы
и перпендикулярен директрисе, а ось
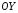 проходит посередине между фокусом и
директрисой. Обозначим через
проходит посередине между фокусом и
директрисой. Обозначим через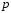 расстояние между фокусом и директрисой.
Тогда
расстояние между фокусом и директрисой.
Тогда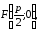 а уравнение директрисы
а уравнение директрисы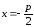 .
.
Число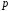 –
называетсяфокальным
параметром
параболы.
Пусть
–
называетсяфокальным
параметром
параболы.
Пусть
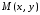 –
текущая точка параболы. Пусть
–
текущая точка параболы. Пусть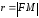 –
фокальный радиус точки
–
фокальный радиус точки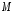 гиперболы.
гиперболы.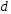 –расстояние
от точки
–расстояние
от точки
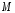 до
директрисы. Тогда
до
директрисы. Тогда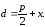 (чертеж
27.)
(чертеж
27.)
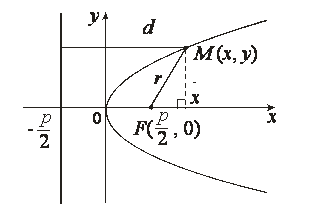
Чертеж 27.
По
определению параболы
 .
Следовательно,
.
Следовательно,
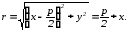
Отсюда:
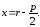
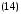
Возведем
уравнение
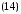 в
квадрат, получим:
в
квадрат, получим:
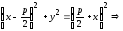
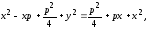
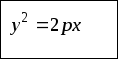 (15)
(15)
где
(15) каноническое
уравнение параболы,
симметричной относительно оси
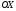 и проходящей через начало координат.
и проходящей через начало координат.
Исследование свойств параболы
1) Вершина параболы:
Уравнению
(15) удовлетворяют числа
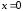 и
и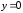 ,
следовательно, парабола проходит через
начало координат.[1.c.109-110]
,
следовательно, парабола проходит через
начало координат.[1.c.109-110]
2) Симметрия параболы:
Пусть
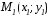 принадлежит параболе, т.е.
принадлежит параболе, т.е. верное
равенство. Точка
верное
равенство. Точка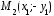 симметрична точке
симметрична точке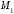 относительно оси
относительно оси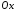 ,
следовательно, парабола симметрична
относительно оси абсцисс. [1.С.110]
,
следовательно, парабола симметрична
относительно оси абсцисс. [1.С.110]
Эксцентриситет параболы:
Определение
4.2. Эксцентриситетом
параболы называется число
 ,
равное единице.
,
равное единице.
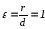 ,
так как по определению параболы
,
так как по определению параболы
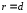 .[1.С.110-111]
.[1.С.110-111]
4) Касательная параболы:
Касательная
к параболе в точке касания
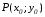 определяется
уравнением
определяется
уравнением
 ,
где
,
где
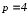 (чертеж
28.)
(чертеж
28.)

Чертеж 28.
Изображение параболы
Построим параболу с вершиной в точке
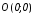 и
и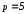 .
.
Построение без использования ИКТ: Для построения параболы задаем прямоугольную систему координат с центром в точке О и единичный отрезок. Отмечаем на оси ОХ фокус
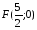 ,так
как
,так
как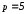 ,
проводим
,
проводим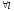 такую, что
такую, что ,
и директрису параболы
,
и директрису параболы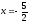 .
Выполняем построение окружности в
точке
.
Выполняем построение окружности в
точке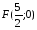 и радиусом равным расстоянию от прямой
и радиусом равным расстоянию от прямой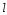 до директрисы параболы. Окружность
пересекает прямую
до директрисы параболы. Окружность
пересекает прямую в точках
в точках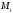 и
и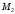 .
Строим параболу так, чтобы она проходила
через начало координат и через точки
.
Строим параболу так, чтобы она проходила
через начало координат и через точки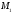 и
и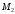 .(чертеж
29.)
.(чертеж
29.)
M1
M2
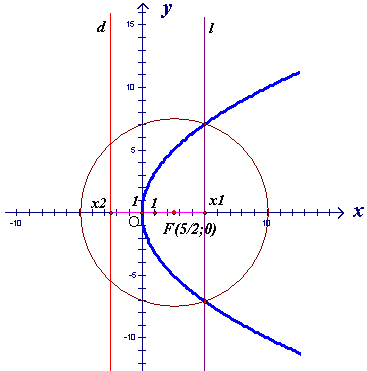
Чертеж 29.
С использованием ЭСО- Mathcad:
Полученное
уравнение имеет вид:
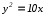 .
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
.
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
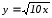 .(чертеж
30.)
.(чертеж
30.)
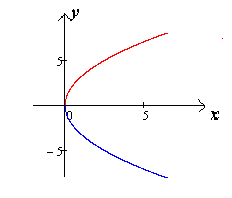
Чертеж 30.
Построим параболу с вершиной в точке
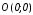 и
и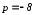 .
.
a)
Построение без использования ИКТ: Для
построения параболы задаем прямоугольную
систему координат с центром в точке О
и единичный отрезок. Отмечаем на оси ОХ
фокус
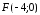 ,так
как
,так
как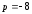 ,
проводим
,
проводим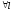 такую, что
такую, что ,
и директрису параболы
,
и директрису параболы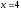 .
Выполняем построение окружности в точке
.
Выполняем построение окружности в точке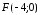 и радиусом равным расстоянию от прямой
и радиусом равным расстоянию от прямой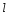 до директрисы параболы. Окружность
пересекает прямую
до директрисы параболы. Окружность
пересекает прямую в точках
в точках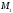 и
и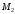 .
Строим параболу так, чтобы она проходила
через начало координат и через точки
.
Строим параболу так, чтобы она проходила
через начало координат и через точки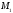 и
и .(чертеж
31.)
.(чертеж
31.)
M1
M2
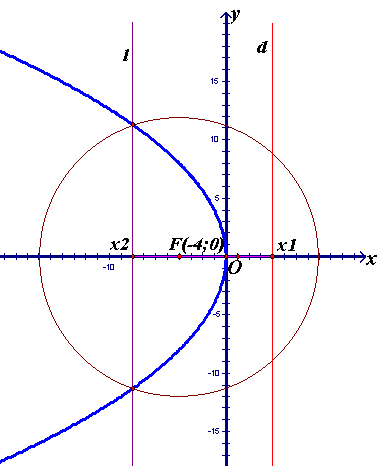
Чертеж 31.
b)С использованием ЭСО- Mathcad:
Полученное
уравнение имеет вид:
 .
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
.
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
 .(чертеж
32.)
.(чертеж
32.)

Чертеж 32.
Чтобы обобщить работу по теории линий второго порядка в элементарной математике и для удобства использования информации о линиях при решении задач, заключим все данные о линиях второго порядка в таблицу № 1.
Таблица №1.
Линии второго порядка в элементарной математике
|
Название линии 2-го порядка
|
Окружность |
Эллипс |
Гипербола |
Парабола |
|
Характеристические свойства |
|
|
|
|
|
Уравнение линии |
|
|
|
|
|
Эксцентриситет |
|
|
|
|
|
Уравнение касательной в точке (x0;y0) |
|
|
|
|
|
Фокус |
|
|
|
|
|
Диаметры линий |
|
|
|
|
Возможности использования ИКТ в изучении линий второго порядка
Процесс информатизации, охвативший сегодня все стороны жизни современного общества, имеет несколько приоритетных направлений, к которым, безусловно, следует отнести информатизацию образования. Она является первоосновой глобальной рационализации интеллектуальной деятельности человека за счет использования информационно-коммуникационных технологий (ИКТ).
Середина 90-х годов прошлого века и до сегодняшнего дня, характеризуется массовостью и доступностью персональных компьютеров в России, широким использованием телекоммуникаций, что позволяет внедрять разрабатываемые информационные технологии обучения в образовательный процесс, совершенствуя и модернизируя его, улучшая качество знаний, повышая мотивацию к обучению, максимально используя принцип индивидуализации обучения. Информационные технологии обучения являются необходимым инструментом на данном этапе информатизации образования.
Информационные технологии не только облегчают доступ к информации и открывают возможности вариативности учебной деятельности, ее индивидуализации и дифференциации, но и позволяют по-новому организовать взаимодействие всех субъектов обучения, построить образовательную систему, в которой ученик был бы активным и равноправным участником образовательной деятельности.
Формирование новых информационных технологий в рамках предметных уроков стимулируют потребность в создании новых программно-методических комплексов направленных на качественное повышение эффективности урока. Поэтому, для успешного и целенаправленного использования в учебном процессе средств информационных технологий, преподаватели должны знать общее описание принципов функционирования и дидактические возможности программно- прикладных средств, а затем, исходя из своего опыта и рекомендаций, "встраивать" их в учебный процесс.
Изучение математики в настоящее время сопряжено с целым рядом особенностей и трудностей развития школьного образования в нашей стране.
Появился так называемый кризис математического образования. Причины его состоят в следующем:
- в изменении приоритетов в обществе и в науке, то есть в настоящее время идет рост приоритета гуманитарных наук;
- в сокращении количества уроков математики в школе;
- в оторванности содержания математического образования от жизни;
- в малом воздействии на чувства и эмоции учащихся.
Сегодня остается открытым вопрос: «Как же наиболее эффективно использовать потенциальные возможности современных информационных и коммуникационных технологий при обучении школьников, в том числе, при обучении математике?».
Компьютер – отличный помощник в изучении такой темы, как “Квадратичная функция”, потому что, используя специальные программы можно строить графики различных функций, исследовать функцию, легко определить координаты точек пересечения, вычислить площади замкнутых фигур и т.д. Например, на уроке алгебры в 9-м классе, посвящённом преобразованию графика (растяжения, сжатия, переносы координатных осей) можно увидеть лишь застывший результат построения, а на экране монитора прослеживается вся динамика последовательных действий учителя и ученика.
Компьютер, как ни одно техническое средство, точно, наглядно и увлекательно открывает перед учеником идеальные математические модели, т.е. то, к чему должен стремиться ребенок в своих практических действиях.
Сколько трудностей приходится испытывать учителю математики для того, чтобы убедить учеников в том, что касательная к графику квадратичной функции в точке касания практически сливается с графиком функции. На компьютере этот факт продемонстрировать очень просто- достаточно сузить интервал по оси Ох и обнаружить, что в очень маленькой окрестности точки касания график функции и касательная совпадают. Все эти действия происходят на глазах у учеников. Этот пример дает толчок к активным размышлениям на уроке. Использование компьютера возможно как в ходе объяснения нового материала на уроке, так и на этапе контроля. При помощи этих программ, например «My Test», ученик самостоятельно может проверить свой уровень знаний по теории, выполнить теоретико-практические задания. Программы удобны своей универсальностью. Они могут быть использованы и для самоконтроля, и для контроля со стороны учителя.
Разумная интеграция математики и компьютерных технологий позволит богаче и глубже взглянуть на процесс решения задачи, ход осмысления математических закономерностей. Кроме того, компьютер поможет сформировать графическую, математическую и мыслительную культуру учеников, а также с помощью компьютера можно подготовить дидактические материалы: карточки, листы опроса, тесты и др. При этом давать возможность ребятам самостоятельно разрабатывать тесты по теме, в ходе чего развивается интерес и творческий подход.
Таким образом, есть необходимость в применении по возможности компьютера на уроках математики более широко, чем есть. Использование информационных технологий будет способствовать повышению качества знаний, расширит горизонты изучения квадратичной функции, а значит, поможет найти новые перспективы для поддержания интереса учащихся к предмету и к теме, а значит и к лучшему, более внимательному отношению к нему. Сегодня современные информационные технологии становятся важнейшим инструментом модернизации школы в целом – от управления до воспитания и обеспечения доступности образования.

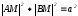
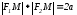
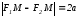
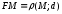

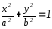
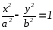
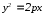

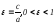

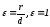
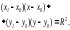
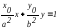
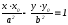
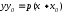
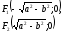
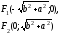
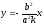 ,
где k-
угловой коэффициент
,
где k-
угловой коэффициент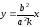 ,
где k
угловой коэффициент
,
где k
угловой коэффициент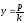 ,
где k
угловой коэффициент
,
где k
угловой коэффициент