
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •Глава II. Практическое применение икт при изучении линий второго порядка
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Линии второго порядка в элементарной математике
- •Вывод уравнения окружности
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Изображение окружности
- •Вывод уравнения эллипса
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •Вывод уравнения гиперболы
- •Исследование свойств гиперболы по ее уравнению
- •1) Пересечение гиперболы с осями координат:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Вывод уравнения параболы
- •Исследование свойств параболы
- •Линии второго порядка в элементарной математике
- •Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
- •Глава II. Практическое применение икт при изучении линий второго порядка
Вывод уравнения эллипса
Введем
прямоугольную систему координат. Пусть
фокусы эллипса лежат на оси Х,
причем
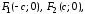 т. Е.
т. Е.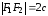 – межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]
– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]
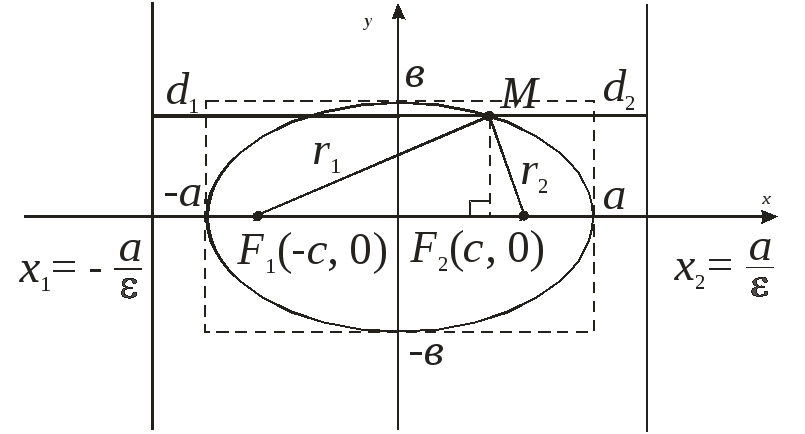
Чертеж 7.
Пусть
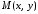 – произвольная точка эллипса. Величины
– произвольная точка эллипса. Величины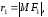
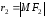 называютсяфокальными
радиусами
точки М
эллипса. По определению эллипса: r1
+ r2
= 2a,
а
> c.
Из прямоугольных треугольников, по
теореме Пифагора, имеем:
называютсяфокальными
радиусами
точки М
эллипса. По определению эллипса: r1
+ r2
= 2a,
а
> c.
Из прямоугольных треугольников, по
теореме Пифагора, имеем:
(2)

Преобразуем
уравнение, умножим уравнение (2) на
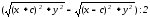 ,
получим:
,
получим:
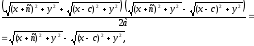
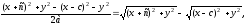
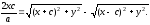 (3)
(3)
Сложим уравнения (2) и (3):
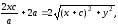
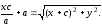 (4)
(4)
Возведем равенство(4) в квадрат, получим:
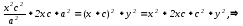
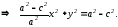
Пусть
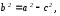 так как
так как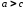
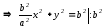 ,
откуда уравнение имеет вид:
,
откуда уравнение имеет вид:
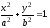
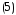
где (5) каноническое уравнение эллипса с центром в начале координат.
Соответственно, отсюда получаем уравнение:
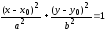
где
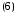 каноническое уравнение эллипса с центром
в точке
каноническое уравнение эллипса с центром
в точке
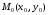 .
Где числа а и b
соответственно большая и малая полуоси
эллипса. Заметим,
что а
>с
Если а
<
.
Где числа а и b
соответственно большая и малая полуоси
эллипса. Заметим,
что а
>с
Если а
<
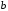 ,
то фокусы эллипса будут лежать на осиОУ,
если а
=
,
то фокусы эллипса будут лежать на осиОУ,
если а
=
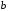 ,
то эллипс превращается в окружность.
,
то эллипс превращается в окружность.
Точки
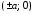 ,
,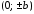 называютсявершинами
эллипса.
Отметим, что эллипс целиком расположен
внутри прямоугольника, ограниченного
прямыми
называютсявершинами
эллипса.
Отметим, что эллипс целиком расположен
внутри прямоугольника, ограниченного
прямыми
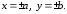
Исследование свойств эллипса по его уравнению
1) Пересечение эллипса с осями координат:
Найдем точки пересечения эллипса с осью ОХ: Пусть y=0, тогда уравнение эллипса имеет вид:
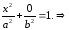
 ,
следовательно
,
следовательно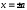 .
.
Отсюда следует, что точки (-a,0),(a,0) являются точками пересечения с осью ОХ.
Найдем точки пересечения эллипса с осью ОУ: Пусть х=0,отсюда имеем:
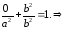
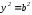 ,
отсюда
,
отсюда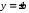 .
.
Следовательно, точки (-b,0),(b,0)являются точками пересечения с осью ОУ.
Отсюда
заключаем, что границы эллипса
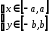 ,
отображающие его схематичное построение.
(чертеж
8.)
[1.С. 105]
,
отображающие его схематичное построение.
(чертеж
8.)
[1.С. 105]
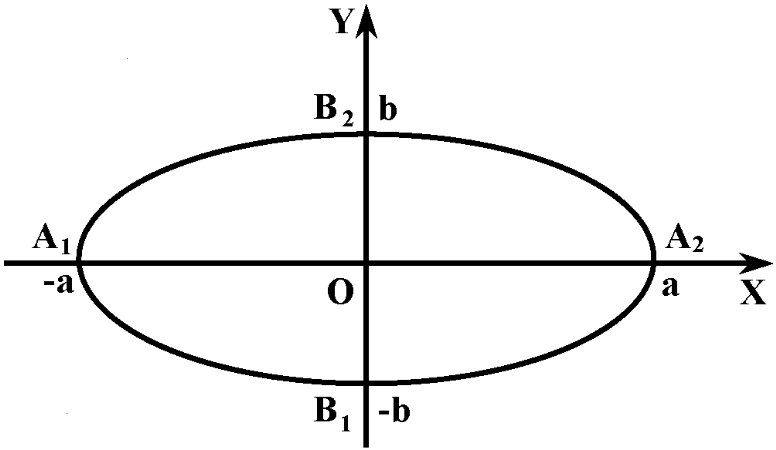
Чертеж 8.
Расстояние |A1A2| = 2a называется большой (фокальной) осью эллипса, расстояние |B1B2| = 2b называется малой осью эллипса. Расстояния от начала координат до вершин A2(a, 0), B2(0, b) называются соответственно большой и малой полуосями эллипса.
Вывод: Таким образом, заключаем, что эллипс вписан в прямоугольник с размерами 2a, 2b (чертеж 9.).
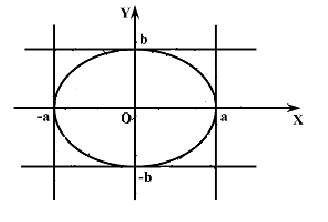
Чертеж 9.
2) Симметрия эллипса относительно координатных осей ox и oy:
Пусть
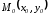 принадлежит эллипсу, т. е
принадлежит эллипсу, т. е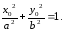 - верное равенство.
- верное равенство.
Точка
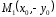 симметрична точке
симметрична точке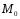 относительно
оси ОХ
относительно
оси ОХ
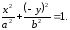
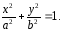 -
верное равенство.
-
верное равенство.
Следовательно,
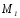 принадлежит эллипсу, отсюда заключаем,
что эллипс симметричен относительно
ОХ
принадлежит эллипсу, отсюда заключаем,
что эллипс симметричен относительно
ОХ
Точка
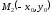 симметрична точке
симметрична точке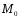 относительно оси ОУ, следовательно,
эллипс симметричен относительно оси
ОУ.
относительно оси ОУ, следовательно,
эллипс симметричен относительно оси
ОУ.
Точка
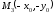 симметрична
точке
симметрична
точке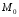 относительно О (центра), следовательно,
эллипс симметричен относительно начала
координат.[1.С.105-106]
относительно О (центра), следовательно,
эллипс симметричен относительно начала
координат.[1.С.105-106]
3) Фокусы эллипса:
Пусть
фокусы эллипса лежат на оси ОX.
Межфокусное расстояние эллипса равно
 причем
причем
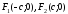 .
Заметим, что
.
Заметим, что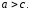
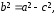
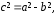
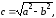

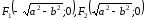 .
[1.С.106]
.
[1.С.106]
4) Эксцентриситет эллипса:
Определение
2.2.
Эксцентриситетом эллипса
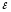 называют отношение межфокусного
расстояния 2с
к длине большой оси 2а.
называют отношение межфокусного
расстояния 2с
к длине большой оси 2а.
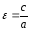 .
.
Так
как
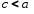 ,
следовательно,
,
следовательно,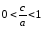 .
.
Если
 стремится к нулю при постоянном значении
стремится к нулю при постоянном значении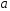 ,
то
,
то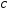 стремится к нулю. При этом величина
стремится к нулю. При этом величина стремится к
стремится к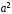 .
В предельном случаи уравнение эллипса
принимает вид:
.
В предельном случаи уравнение эллипса
принимает вид: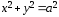 .
Это уравнение окружности. Если
.
Это уравнение окружности. Если ,
то
,
то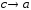 .
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]
.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]
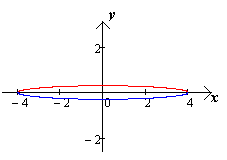
Чертеж 10.
5) Диаметры эллипса:
Всякая
хорда, проходящая через центр эллипса,
называется диаметром
эллипса.
В частности, диаметрами эллипса является
его большая ось
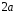 и
малая ось
и
малая ось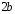 .
Всякий диаметр эллипса, не являющийся
его осью, больше малой оси, но меньше
большой оси (чертеж
11.).
[1.С.106-107]
.
Всякий диаметр эллипса, не являющийся
его осью, больше малой оси, но меньше
большой оси (чертеж
11.).
[1.С.106-107]
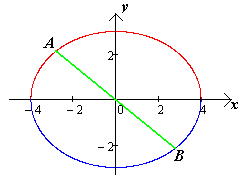
Чертеж 11.
6) Касательная к эллипсу:
Уравнение
касательной к эллипсу
 где
где -
координаты точки касания и
-
координаты точки касания и соответственно большая и меньшая полуоси
эллипса (чертеж
12.).
соответственно большая и меньшая полуоси
эллипса (чертеж
12.).
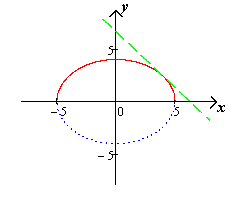
Чертеж 12.
7) Частный случай эллипса - окружность:
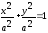
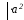
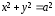 ,
где
,
где
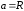 окружности.
окружности.
8) Взаимное расположение точек и эллипса:
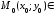 эллипсу,
если
эллипсу,
если
 верное
равенство,
верное
равенство,
Если
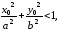 то
то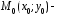 лежит
внутри эллипса,
лежит
внутри эллипса,
Если
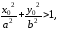 то
то лежит
вне эллипса. [1.С.100]
лежит
вне эллипса. [1.С.100]
Изображение эллипса
Построим эллипс с центром в точке
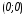 и с большей осью равной 14 и меньшей осью
равной 10.
и с большей осью равной 14 и меньшей осью
равной 10.
Построение без использования ИКТ: Для построения эллипса построим прямоугольную систему координат с центром в точке О и единичный отрезок. Построим прямоугольник со сторонами 2a=14,2b=10 и впишем в него эллипс так, чтобы координаты точек (-7;0),(7;0),(0;-5),(0;5) принадлежали эллипсу.(чертеж 13.)
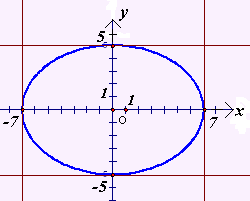
Чертеж 13.
С использованием ЭСО- Mathcad:
Полученное
уравнение эллипса имеет вид:
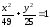 .
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
.
Для построения линии второго порядка
в программеMathcad
приводим уравнение к виду:
 (чертеж
14.)
(чертеж
14.)
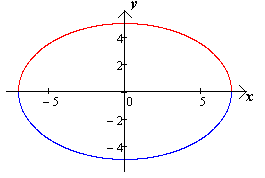
Чертеж 14.
Дано параметрическое уравнение эллипса
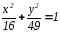 ,
построить данную линию второго порядка.
,
построить данную линию второго порядка.
Построение без использования ИКТ: Для построения эллипса построим прямоугольную систему координат с центром в точке О и единичный отрезок. Построим прямоугольник со сторонами 2a=8,2b=14 и впишем в него эллипс так, чтобы координаты точек (-4;0),(4;0),(0;-7),(0;7) принадлежали эллипсу.(чертеж 15.)

Чертеж 15.
С использованием ЭСО- Mathcad:
Для
построения линии в Mathcad
приведем ее к виду:
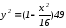 ,
,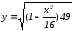 .(чертеж
16.)
.(чертеж
16.)
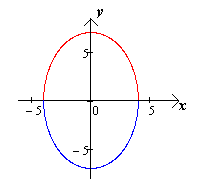
Чертеж 16.
ГИПЕРБОЛА
Определение
3.1.
Гипербола -
множество точек плоскости, модуль
разности расстояний от
которых
до двух данных точек
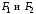 этой плоскости, называемых фокусами
гиперболы, есть заданная постоянная
величина
этой плоскости, называемых фокусами
гиперболы, есть заданная постоянная
величина меньшая,
чем расстояние между фокусами
меньшая,
чем расстояние между фокусами
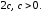 [8.С.510]
[8.С.510]
