
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •Глава II. Практическое применение икт при изучении линий второго порядка
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Линии второго порядка в элементарной математике
- •Вывод уравнения окружности
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Изображение окружности
- •Вывод уравнения эллипса
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •Вывод уравнения гиперболы
- •Исследование свойств гиперболы по ее уравнению
- •1) Пересечение гиперболы с осями координат:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Вывод уравнения параболы
- •Исследование свойств параболы
- •Линии второго порядка в элементарной математике
- •Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
- •Глава II. Практическое применение икт при изучении линий второго порядка
СОДЕРЖАНИЕ
Введение
Глава I. Теоретические и методические аспекты изучения линий второго порядка
Пункт 1.1. Теория линий второго порядка и использования ИКТ в обучении
Понятие линии второго порядка в аналитической геометрии
Линии второго порядка в элементарной математике
Возможности использования ИКТ в изучении линий второго порядка
Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
1.2.1. Методика изучения линий второго порядка в школьном курсе алгебры
1.2.2. Анализ комплектов учебников под редакцией Г. В. Дорофеева и Ш. Ф. Алимова
Глава II. Практическое применение икт при изучении линий второго порядка
2.1. Методика использования ИКТ в изучении линий второго порядка на уроках алгебры
2.2. Систематизация ЦОР, содержащих линии второго порядка
2.3. Элективный курс
Заключение
Литература
Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
Понятие линии второго порядка в аналитической геометрии
Аналитическая
геометрия на плоскости занимается
подробным изучением геометрических
свойств эллипса,
гиперболы
и параболы,
представляющих собой линии пересечения
кругового конуса с плоскостями, не
проходящими через его вершину.
В аналитической
геометрии
систематически исследуются так называемые
алгебраические линии второго порядка
(эти линии в декартовых прямоугольных
координатах определяются соответственно
алгебраическими уравнениями второй
степени). Линии второго порядка
определяются уравнениями вида
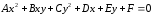 .
Основной метод исследования и классификации
этих линий заключается в подборе такой
декартовой прямоугольной системы
координат, в которой уравнение линии
имеет наиболее простой вид, и последующем
исследовании этого простого уравнения.
.
Основной метод исследования и классификации
этих линий заключается в подборе такой
декартовой прямоугольной системы
координат, в которой уравнение линии
имеет наиболее простой вид, и последующем
исследовании этого простого уравнения.
Определение
1. Линией
второго порядка
называется множество всех точек
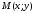 плоскости, координаты которых удовлетворяют
уравнению:
плоскости, координаты которых удовлетворяют
уравнению:
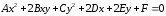
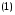
где
A,B,C,D,E,F — вещественные коэффициенты,
причем
 .
.
Исследуем уравнение и узнаем, что представляет собой произвольная линия
второго порядка.
Приведение общего уравнения линии второго порядка к каноническому виду
Рассмотрим уравнение (1) и приведем его к такой системе координат, в которой уравнение имело бы наиболее простой вид. Существует такая система координат, в которой уравнение (1) не содержит произведения xy, то есть B = 0.
Осуществим
параллельный перенос исходной системы
координат XOY
на вектор
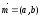 (рис.1). Возьмем точкуM
с координатами
(рис.1). Возьмем точкуM
с координатами
 в
системе координат
в
системе координат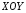 .
Тогда в новой системе координат
.
Тогда в новой системе координат координаты
координаты точкаM
находятся по формулам:
точкаM
находятся по формулам:
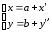 откуда
откуда
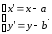
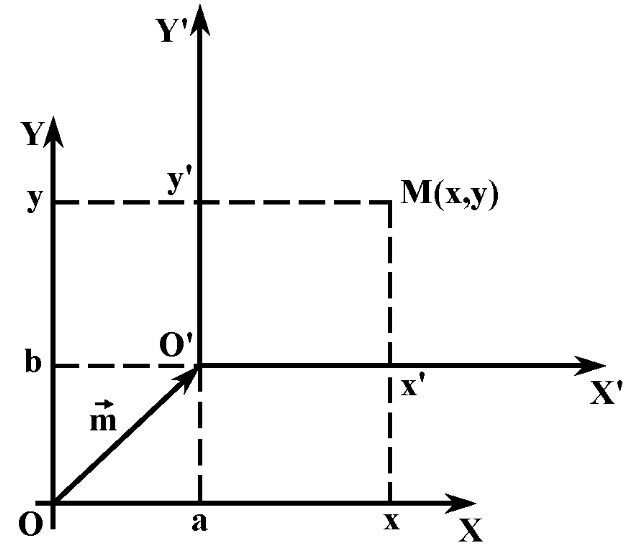
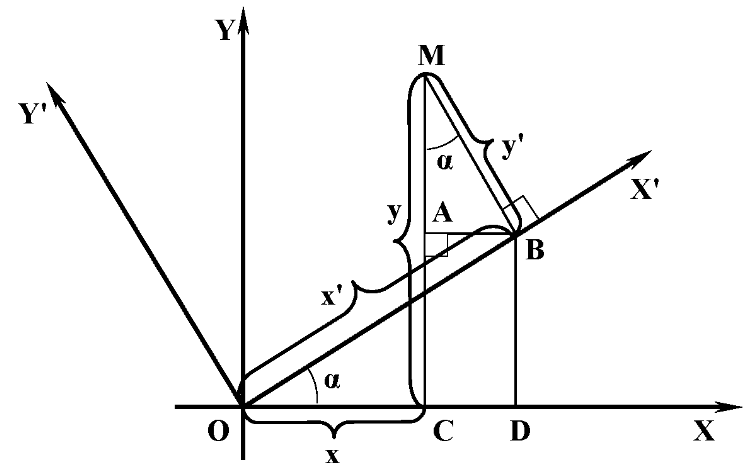
Рис. 1. Рис.2.
Пусть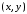 координаты точкиM
в системе координат XOY.
Повернем оси координат на угол
координаты точкиM
в системе координат XOY.
Повернем оси координат на угол
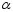 в положительном направлении и обозначим
(x', y') координаты точкиM
в новой системе координат X'OY'.(рис.2.)
Найдем связь между этими координатами.
Очевидно, что:
в положительном направлении и обозначим
(x', y') координаты точкиM
в новой системе координат X'OY'.(рис.2.)
Найдем связь между этими координатами.
Очевидно, что:
 (так
как
(так
как
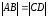 );
(2)
);
(2)
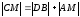 (так
как
(так
как
 );
(3)
);
(3)
Рассмотрим
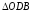 .
Так как он прямоугольный, то
.
Так как он прямоугольный, то ,
, .
(4)
.
(4)
Рассмотрим
теперь
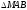 .
Он также прямоугольный, поэтому
.
Он также прямоугольный, поэтому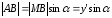 ,
, .
(5)
.
(5)
Таким
образом, с учетом того, что
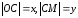 ,
из равенств (2)-(5) получим:
,
из равенств (2)-(5) получим: (6)
(6)
Следовательно,
система (6) представляет собой выражение
старых координат
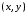 через
новые
через
новые .
.
Замечание. Для того чтобы получить выражение новых координат через старые, достаточно угол α в формулах (6) заменить на угол (−α), так как при повороте системы координат X′OY ′ на угол (−α) мы получим систему XOY .
Подставим формулы (6) у уравнение (1), получим:
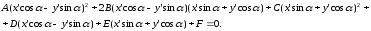 Соберем
коэффициенты при соответствующих
неизвестных.
Соберем
коэффициенты при соответствующих
неизвестных.
При
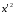 ,
получим:
,
получим:
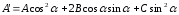 ,
,
При
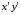 :
:
 ,
(7)
,
(7)
При
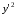 :
:
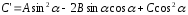 ,
,
При
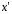 :
:
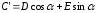 ,
,
При
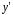 :
:
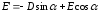 .
.
Таким образом, уравнение (1) с учётом замены (6) принимает вид:
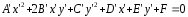 (8)
(8)
Подберем
угол
 таким
образом, чтобы коэффициент
таким
образом, чтобы коэффициент .
Из (7) следует, что
.
Из (7) следует, что поэтому
поэтому
После данного преобразования уравнение (1) примет вид:
 .
(9)
.
(9)
Задача 1. Доказать, что при повороте на любой угол α имеет место равенство:
 (10)
(10)
Определение 2. Величины, которые не меняются при преобразованиях, называются инвариантными.
Так
как мы подобрали угол α так, что
 ,
то из (10) следует, что
,
то из (10) следует, что
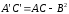 .
(11)
.
(11)
Чтобы проанализировать уравнение кривой (9), рассмотрим три
случая:
1)
 (эллиптический случай);
(эллиптический случай);
2)
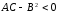 (гиперболический случай);
(гиперболический случай);
3)
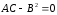 (параболический случай).
(параболический случай).
Подробнее
рассмотрим эллиптический случай.
Из
 следует,
что
следует,
что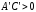 ,
то есть знаки
,
то есть знаки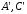 совпадают.
Пусть A′ > 0, C′ > 0. Выделим полные
квадраты при неизвестных x′, y′, получим:
совпадают.
Пусть A′ > 0, C′ > 0. Выделим полные
квадраты при неизвестных x′, y′, получим:
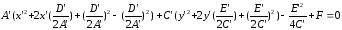
Дополним члены, содержащие x’ и y’,до полного квадрата:
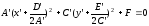 ,
(12)
,
(12)
где

Положим
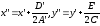 ,
тогда уравнение (12) примет вид:
,
тогда уравнение (12) примет вид: .
(13)
.
(13)
Пусть
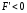 .
Разделим обе части уравнения (13) на
.
Разделим обе части уравнения (13) на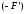 ,
получим:
,
получим:
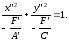 (14)
(14)
Так
как
 и
и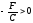 ,
то предположим, что
,
то предположим, что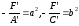 .
(15)
.
(15)
Из
(14) и (15) следует, что мы получили
каноническое уравнение эллипса

Пусть F′ > 0, тогда в уравнении (13) слева стоит неотрицательное число, а справа - отрицательное, поэтому точек, удовлетворяющих данному уравнению, не существует.
Пусть F′ = 0. Тогда уравнению (13) удовлетворяет только одна точка
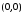 ,
то есть точка с координатами
,
то есть точка с координатами
Рассмотрим
гиперболический случай. Из
 следует, что
следует, что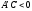 ,
то есть числа
,
то есть числа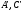 имеют
разные знаки. Выполняя аналогичные
преобразования, как и для эллиптического
случая, получим уравнение кривой:
имеют
разные знаки. Выполняя аналогичные
преобразования, как и для эллиптического
случая, получим уравнение кривой:
Предположим, что
 .
Отсюда:
.
Отсюда:
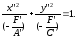 (16)
(16)
Так
как
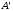 и
и
 разных знаков, следовательно , одна из
скобок больше нуля, другая скобка меньше
нуля. Пусть
разных знаков, следовательно , одна из
скобок больше нуля, другая скобка меньше
нуля. Пусть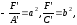 (17)
(17)
тогда мы получаем каноническое уравнение гиперболы:
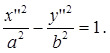
При
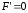 уравнение принимает вид:
уравнение принимает вид: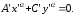 (18)
(18)
Пусть
 ,
тогда
,
тогда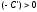 и уравнение (18) примет вид:
и уравнение (18) примет вид: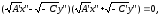 откуда
откуда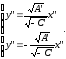 Таким образом, получили уравнения двух
пересекающихся прямых.
Таким образом, получили уравнения двух
пересекающихся прямых.
Рассмотрим
параболический случай. Так
как
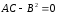 ,
то
,
то .
.
Пусть
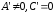 .
Так как после поворота
.
Так как после поворота ,
то уравнение (9) преобразуется до вида:
,
то уравнение (9) преобразуется до вида: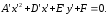 (19)
(19)
Соберём
члены, содержащие
 ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
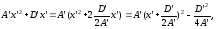 тогда
уравнение (19) примет вид:
тогда
уравнение (19) примет вид:
 или
или ,
(20)
,
(20)
где
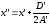 .
Из (20) следует, что
.
Из (20) следует, что
Рассмотрим два случая:
Пусть
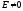 ,
тогда
,
тогда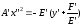 ,
то есть
,
то есть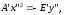 (21)
(21)
где

Положим
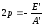 ,
тогда уравнение (21) примет вид:
,
тогда уравнение (21) примет вид:
Это каноническое уравнение параболы, симметричной относительно
оси (OY ).
Пусть
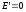 ,
тогда уравнение (20) перепишется в виде
,
тогда уравнение (20) перепишется в виде
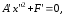 (22)
(22)
1.
Если
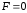 ,
то получим уравнение оси (OY )
,
то получим уравнение оси (OY )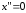 .
.
2.
Если
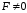 ,
то возможны два случая. Если A′ и F′
одного знака, то точек, удовлетворяющих
данному уравнению, нет; если же A′ и F′
разных знаков, то
,
то возможны два случая. Если A′ и F′
одного знака, то точек, удовлетворяющих
данному уравнению, нет; если же A′ и F′
разных знаков, то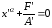 ,
где
,
где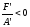 ,
поэтому
,
поэтому и уравнение (22) описывает две параллельные
прямые:
и уравнение (22) описывает две параллельные
прямые:
b)
Пусть
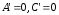 ,
тогда уравнение (9) примет вид
,
тогда уравнение (9) примет вид
 (23)
(23)
Если
 ,
а
,
а ,
то точек, удовлетворяющих уравнению
(23), нет; если же
,
то точек, удовлетворяющих уравнению
(23), нет; если же или
или отличны от нуля, то уравнение (23) описывает
прямую.
отличны от нуля, то уравнение (23) описывает
прямую.
Вывод. Путем преобразований кривой второго порядка, определяемой уравнением (1) мы можем получить уравнения таких линии второго порядка, как:
 -
уравнение эллипса
-
уравнение эллипса -
уравнение гиперболы
-
уравнение гиперболы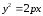 -
уравнение параболы
-
уравнение параболы
