Математика / Теория / 2 предел
.doc
Лекция 2.
Теория предела.
Числовые последовательности.
Опр. Функция, заданная на множестве натуральных чисел, называется числовой последовательностью.
Т. е., если каждому
натуральному числу n
поставлено в соответствие определенное
число
,
то говорят, что задана числовая
последовательность
:
1 2 3 … n … - аргумент
…
… - члены
последовательности.
- общий член последовательности. Чтобы задать числовую последовательность, необходимо указать формулу ее общего члена. Примеры числовых последовательностей:
:
2, 4, 8, …..,
,…,
:
,
,
,
…,
,
… и т.д.
Предел числовой последовательности.
Рассмотрим числовую
последовательность
.
Изобразим ее на числовой оси.
Очевидно, что члены последовательности убывают по величине, но при этом положительны и не равны нулю. При достаточно больших номерах члены последовательности будут сколь угодно близкими к 0. В этом случае говорят, что 0 является пределом данной числовой последовательности.
Опр.
Число А
называется пределом числовой
последовательности
,
если для любого, даже сколь угодно малого
положительного числа
,
найдется такой номер N,
зависящий от
,
что для всех членов последовательности
с номерами n>N,
верно неравенство:
.
Если последовательность
имеет предел, равный А,
то она называется сходящейся к числу А
(в противном случае – расходящейся).
Кратко это можно записать так:
.
(Или так:
).
Используя логические символы, определение предела числовой последовательности можно записать так:
.
Смысл определения состоит в том, что при достаточно больших номерах все члены последовательности (начиная с некоторого), будут заключены в - окрестности предельной точки, какой бы узкой она ни была.
Замечание. Числовая
последовательность может иметь предел,
равный
,
а может не иметь предела вообще.
Пример.
;
.
Предел функции.
Предел функции в точке.
Односторонние пределы.
Пример.
Пусть функция
y=f(x)
задана в некоторой окрестности точки
,
за исключением, быть может, самой точки
.
Опр. 1.
Точка А
называется пределом функции y=f(x)
при
,
если для любой последовательности точек
,
сходящейся к
,
последовательность значений функции
сходится к А.
В этом случае пишут:
=А,
или
при
.
Это определение называют определением предела по Гейне (нем. математик XIX в.)
Замечание.
Если точка
,
то предел
,
если он существует, равен значению
функции в данной точке
.
(См. рис.1)
Опр. 2.
Если при стремлении к
x
принимает
лишь значения, меньшие (большие)
,
и при этом
,
то говорят об одностороннем пределе
слева
(справа
).
Пример.
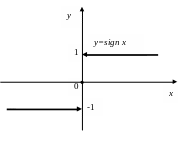
Утверждение. Предел функции в точке существует тогда и только тогда, когда существуют и равны оба односторонних предела функции в данной точке.
Существует и другое (равносильное) определение предела функции, в котором используется понятие окрестности. Оно называется определением по Коши.
Опр. 3.
Число А
называется пределом функции y=f(x)
при
,
если для любого, даже сколь угодно малого
положительного числа
,
найдется такое положительное число
,
зависящее от
,
что для всех x,
удовлетворяющих условию
,
верно неравенство
.
В символической форме это определение записывается так:
.
Вопрос. Где здесь окрестности? Раскрыть скобки в неравенствах.
Опр.3 можно также сформулировать в следующем общем виде:
Число А
называют пределом функции y=f(x)
при
и пишут
=А,
если
.
Геометрический смысл данного определения 3 заключается в следующем: какую бы (даже сколь угодно малую) окрестность точки А на оси Оу мы ни взяли, всегда найдется окрестность точки на оси Ох, являющаяся ее прообразом.
Бесконечные пределы.
Общее определение
предела позволяет дать определение и
для случаев, когда
или А являются несобственными точками,
т.е.
.
Опр. 4.
Число А
называют пределом функции y=f(x)
при
и пишут
=А,
если:
.
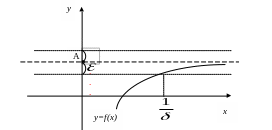
Опр. 5.
Число А
называют пределом функции y=f(x)
при
и пишут
=А,
если:
.
Самостоятельно: сформулировать
определение предела при
.
Опр.6.
Говорят, что функция y=f(x)
имеет предел при
,
равный
и пишут
,
если:
.
Самостоятельно: сформулировать
определение предела, равного
.
3. Бесконечно малые и бесконечно большие функции, их связь.
Опр.
Функция
называется бесконечно малой при
функцией, если ее предел при
равен нулю:
=0
.
Опр.
Функция
называется бесконечно большой при
функцией, если ее предел при
есть несобственное число:
=
.
Пример. Функция
является: БМ при
;
ББ при
;
не является ни БМ, ни ББ при
.
Теорема 1. (о связи предела и бесконечно малой функции). Если функция
y=f(x)
имеет предел
,
то разность между функцией и значением
ее предела есть бесконечно малая при
.
Док-во. Имеем:
=А .
Надо доказать, что
-А)=0,
т.е.
.
Очевидно, что это условие выполнено. ▲
Следствие. Если
функция y=f(x)
имеет предел
,
то ее можно представить в виде суммы
этого числа А
и бесконечно малой при
функции
:
.
Теорема 2 ( о
связи БМ и ББ функций).
Если
есть БМ
Ф,
и
в некоторой окрестности точки
,
то функция
есть ББ
Ф.
Если
есть ББ
Ф,
то функция
есть БМ
Ф.
Доказать самостоятельно, используя определение предела.
4. Свойства бесконечно больших и бесконечно малых функций.
Свойства бесконечно малых функций.
1. Алгебраическая сумма конечного числа БМ Ф есть БМФ при .
2. Произведение БМ Ф на ограниченную в некоторой окрестности точки функцию (в т.ч. на постоянную, на другую БМ) есть БМ Ф.
3. Частное от деления БМ Ф на функцию, предел которой отличен от нуля, есть БМ Ф.
Замечание. Свойство 3 не рассматривает предел отношения двух БМ Ф из-за его неопределенности: он может быть равен как конечному числу, так и .
Докажем, например, свойство 1.
Пусть
и
есть БМ
Ф.
Докажем, что функция
также есть БМ
Ф.
По условию для
любого
,
а значит, и для
найдутся такие числа
и
,
что
:
если
,
то
(1)
если
,
то
(2)
Если в качестве
взять минимальное из
и
,
т.е.
,
то для всех х,
удовлетворяющих условию
будут верны оба неравенства (1) и (2).
Складывая их почленно, получим:
.
Используя первое неравенство треугольника, перейдем к более сильному неравенству:
.
Итак,
мы нашли
,
такое, что при всех
выполняется неравенство
.
Это и означает, что функция
есть БМ
Ф.
▲
Свойства бесконечно больших функций.
1. Произведение ББ Ф на функцию, предел которой отличен от 0, есть ББ Ф.
2. Сумма ББ Ф и ограниченной функции есть ББ Ф.
3. Сумма ББ Ф одного знака есть ББ Ф того же знака.
4. Частное от деления ББ Ф на функцию, имеющую конечный предел, есть ББ Ф.
Сравнение бесконечно малых функций.
Пусть и - БМ Ф. Предположим, что существует предел их отношения, равный некоторому значению А (собств. или несобств.), т.е.
.
Тогда если:
А – число, не равное 0 или 1, то функции и называются БМ одинакового порядка.
А=0, то функция называется БМ более высокого порядка малости, чем и обозначают:
(о малое).
Пример:
,
- БМ при х→0,
А=
,
то функция
называется БМ более высокого порядка
малости, чем
.А =1, то функции и называются эквивалентными БМ , обозначается:
~
.
Свойства эквивалентных БМ
1. ~ ↔ ~ (рефлексивность)
2.
~
,
~
↔
~
(транзитивность)
3.
~
→
эквивалентные БМ отличаются друг от
друга на БМ высшего порядка малости.
4. Под знаком предела в отношении или произведении БМ можно заменять эквивалентными БМ. Например,
.
,
.
Таблица
эквивалентности БМ для
~
~
~
~
~
~
~
lna
ln(1+ )~
~
p
Пример.
.
Замечание. Те же понятия имеют место для ББ величин, только термин «порядок малости» заменяется на термин «порядок роста».